Bài giảng Xử lý ảnh
64
GV. Mai Cường Thọ
Có r
ấ
t nhi
ề
u k
ỹ
thu
ậ
t ch
ọ
n ng
ưỡ
ng t
ự
độ
ng xu
ấ
t phát t
ừ
l
ượ
c
đồ
xám. Nh
ữ
ng k
ỹ
thu
ậ
t ph
ổ
bi
ế
n nh
ấ
t trong s
ố
đ
ó s
ẽ
đượ
c trình bày d
ướ
i
đ
ây. Nh
ữ
ng k
ỹ
thu
ậ
t này có
th
ể
t
ậ
n d
ụ
ng l
ợ
i th
ế
do s
ự
làm tr
ơ
n d
ữ
li
ệ
u l
ượ
c
đồ
ban
đầ
u mang l
ạ
i, nh
ằ
m lo
ạ
i b
ỏ
nh
ữ
ng dao
độ
ng nh
ỏ
v
ề
độ
sáng. Tuy nhiên các thu
ậ
t toán làm tr
ơ
n c
ầ
n ph
ả
i c
ẩ
n
tr
ọ
ng không
đượ
c làm d
ị
ch chuy
ể
n các v
ị
trí
đỉ
nh c
ủ
a l
ượ
c
đồ
. Nh
ậ
n xét này d
ẫ
n
đế
n
thu
ậ
t toán làm tr
ơ
n l
ượ
c
đồ
d
ướ
i dây, v
ớ
i
độ
r
ộ
ng c
ủ
a c
ử
a s
ổ
W là N, thông d
ụ
ng là
N=3 ho
ặ
c N=5 (b
ộ
l
ọ
c trung bình 1-chi
ề
u):
[ ]
( )
(
)
[ ]
ibh
N
bh
N
Ni
rawsmooth
−=
∑
−
−−=
2/1
2/1
1
2.1.
Tuật toán đẳng liệu (Isodata)
K
ỹ
thu
ậ
t ch
ọ
n ng
ưỡ
ng theo ki
ể
u l
ặ
p này do Ridler và Calvard
đư
a ra. Thu
ậ
t
toán nh
ư
sau:
- Chia l
ượ
c
đồ
thành 2
đ
o
ạ
n b
ằ
ng m
ộ
t giá tr
ị
ng
ưỡ
ng kh
ở
i
độ
ng
1
0
2
−
=
B
θ
, t
ứ
c
là b
ằ
ng ph
ầ
n n
ử
a thang
độ
xám
độ
ng c
ủ
a
ả
nh.
- Sau
đ
ó tính toán
độ
sáng trung bình c
ủ
a 2 vùng:
-
0,f
m
c
ủ
a nh
ữ
ng
đ
i
ể
m
ả
nh thu
ộ
c
đố
i t
ượ
ng
-
0,b
m
c
ủ
a nh
ữ
ng
đ
i
ể
m
ả
nh n
ề
n.
- Tính giá tr
ị
ng
ưỡ
ng m
ớ
i
2
0,0,
1
bf
mm
+
=θ
Quá trình này c
ứ
th
ế
s
ẽ
đượ
c ti
ế
p t
ụ
c v
ớ
i các ng
ưỡ
ng m
ớ
i cho
đế
n khi nào giá
tr
ị
ng
ưỡ
ng không thay
đổ
i n
ữ
a thì d
ừ
ng l
ạ
i. Bi
ể
u di
ễ
n d
ướ
i d
ạ
ng công th
ứ
c toán h
ọ
c,
chúng ta có:
2
1,1, −−
+
=
kbkf
k
mm
θ
cho t
ớ
i khi
1−
=
kk
θθ
2.2.
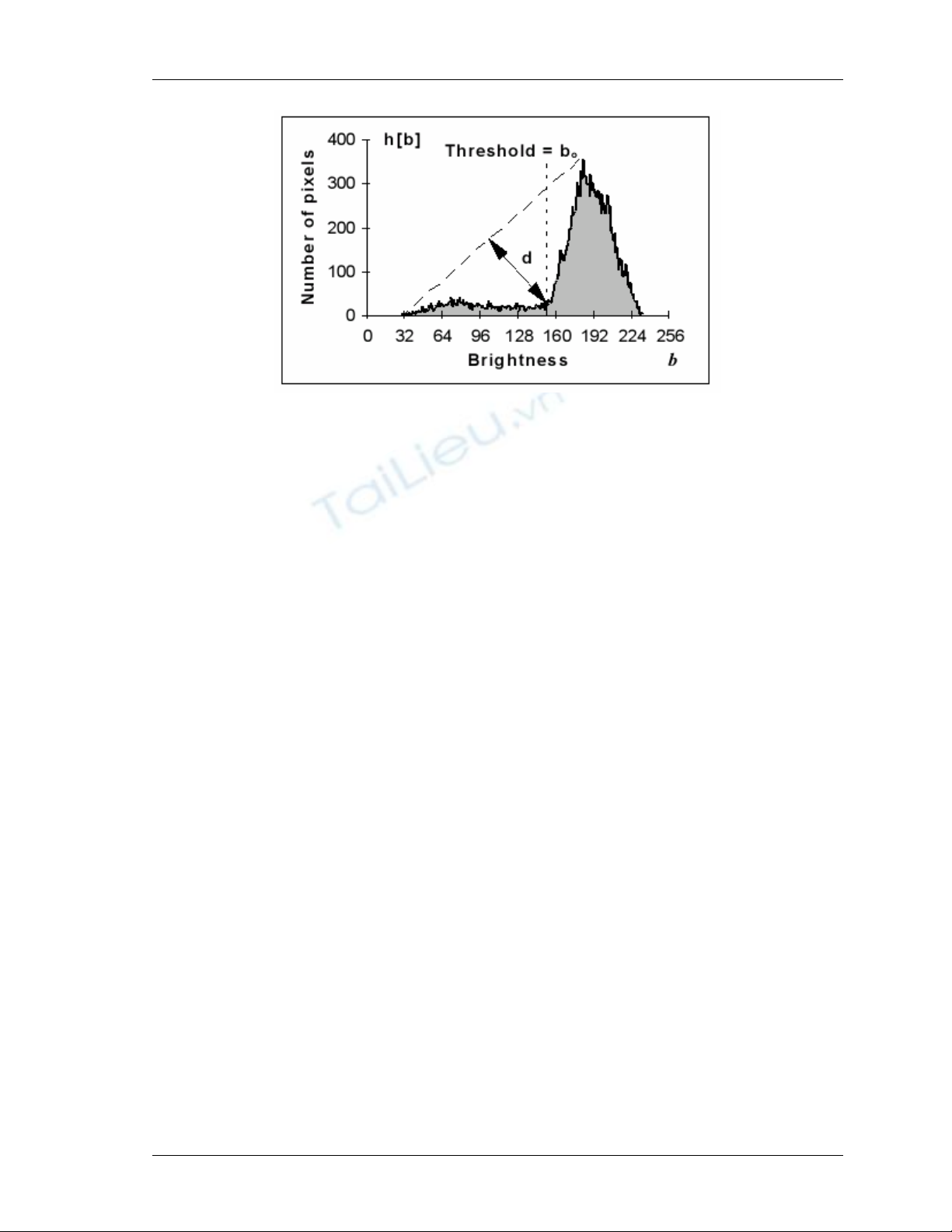
Thuật toán tam giác
Thu
ậ
t toán này do Zack
đư
a ra trong (36) và
đượ
c minh h
ọ
a trong hình (trang
bên). Trong hình này, chúng ta có th
ể
quan sát th
ấ
y m
ộ
t
đườ
ng th
ẳ
ng
đ
ã
đượ
c xây
d
ự
ng b
ằ
ng cách n
ố
i t
ừ
giá tr
ị
l
ớ
n nh
ấ
t c
ủ
a l
ượ
c
đồ
t
ạ
i
độ
sáng b
max
đế
n giá tr
ị
nh
ỏ
nh
ấ
t c
ủ
a l
ượ
c
đồ
t
ạ
i
độ
sáng b
min
.V
ớ
i m
ỗ
i
độ
sáng b trong kho
ả
ng [b
max
, b
min
], chúng
ta
đ
i tính kho
ả
ng cách d t
ừ
giá tr
ị
l
ượ
c
đồ
t
ạ
i b là h[b]
đế
n
đườ
ng th
ẳ
ng
đ
ã có. Giá tr
ị
b
0
ứ
ng v
ớ
i kho
ả
ng cách l
ớ
n nh
ấ
t s
ẽ
đượ
c ch
ọ
n làm giá tr
ị
ng
ưỡ
ng
θ
.
Bài giảng Xử lý ảnh
65
GV. Mai Cường Thọ
K
ỹ
thu
ậ
t l
ấ
y ng
ưỡ
ng không nh
ấ
t thiét ph
ả
i
đượ
c áp d
ụ
ng cho toàn b
ộ
ả
nh, mà
có th
ể
áp d
ụ
ng cho t
ừ
ng vùng
ả
nh m
ộ
t. Hai tác gi
ả
Chow và Kaneko
đ
ã phát tri
ể
n
m
ộ
t bi
ế
n th
ể
c
ủ
a k
ỹ
thu
ậ
t l
ấ
y ng
ưỡ
ng b
ằ
ng cách chia m
ộ
t
ả
nh có kích th
ướ
c M
x
N ra
thành nhi
ề
u vùng không ch
ồ
ng ch
ấ
t lên nhau. Các giá tr
ị
ng
ưỡ
ng
đượ
c tính riêng
bi
ệ
t cho t
ừ
ng vùng m
ộ
t và sau
đ
ó
đượ
c k
ế
t h
ợ
p l
ạ
i thông qua phép n
ộ
i suy
để
hình
thành nên m
ộ
t m
ặ
t ng
ưỡ
ng cho toàn b
ộ
ả
nh. Trong thu
ậ
t toán m
ớ
i này, kích th
ướ
c
c
ủ
a các vùng c
ầ
n
đượ
c ch
ọ
n m
ộ
t cách thích h
ợ
p sao cho có m
ộ
t l
ượ
ng
đ
áng k
ể
các
đ
i
ể
m
ả
nh
ở
trong m
ộ
t vùng, nh
ằ
m ph
ụ
c v
ụ
cho vi
ệ
c tính l
ượ
c
đồ
và xác
đị
nh ng
ưỡ
ng
t
ươ
ng
ứ
ng. Tính h
ữ
u ích c
ủ
a thu
ậ
t toán này, c
ũ
ng nh
ư
nhiêu thu
ậ
t toán khác, s
ẽ
ph
ụ
thu
ộ
c vào t
ừ
ng
ứ
ng d
ụ
ng c
ụ
th
ể
.