Bài giảng Xử lý ảnh
57
GV. Mai Cường Thọ
Quá trình dò biên theo nền vùng là: tìm 1 dãy các điểm (n
0
, v
0
), (n
1
, v
1
)…(n
k
, v
k
) sao
cho
n
0,
n
1,
….n
k
: chu tuyến nền
v
0
, v
1
, ….v
k
: chu tuyến vùng
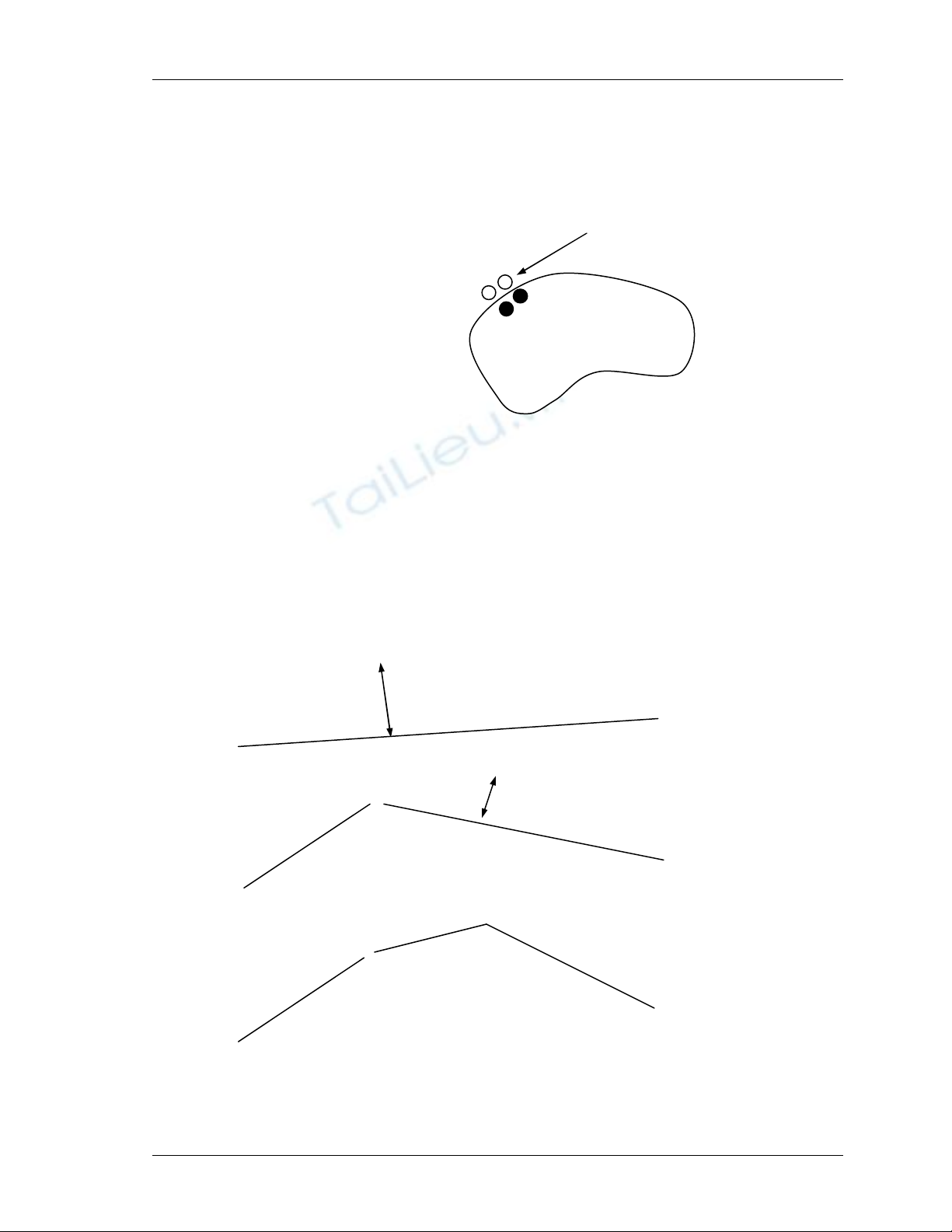
3. Xấp xỉ bởi đoạn thẳng
Nối điểm xuất phát R với điểm đang xét P
c
bởi một đoạn thẳng. Sau đó tính
toạ độ của P
i
, một điểm nằm giữa R và P
c
sao cho khoảng cách từ P
i
đến đoạn thẳng
là cực đại. Gọi khoảng cách này là d
i
. Nếu d
i
lớn hơn một ngưỡng cho trước (độ
chính xác của xấp xỉ) người ta phân đoạn RP
c
thành 2 đoạn RP
i
và P
i
P
c
và tiếp tục
thực hiện lấy mẫu với từng đoạn cho tới khi đoạn thẳng tìm được là “rất gần” với
đường bao.
0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 1 1 1 1 1 1 1 0 0 0
0 0 0 1 1 1 1 1 1 1 1 1 0 0
0 0 0 1 1 1 1 1 1 1 1 1 0 0
0 0 0 1 1 1 1 1 1 1 1 0 0 0
0 0 0 1 1 1 1 1 1 1 0 0 0 0
0 0 0 0 1 1 1 1 1 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0
Cặp (n
i+1
, v
i+1
) 8 láng giềng
P
i
•
•
•
•
•
•
•
•
•
•
•
•
R
P
c
d
i
P
i
d
i
•
•
•
•
•
•
•
•
•
•
•
•
R
P
c
P
1
P
2
•
•
•
•
•
•
•
•
•
•
•
•
R
P
c
Hình xấp xỉ đường biên bằng đường gấp khúc
Bài giảng Xử lý ảnh
58
GV. Mai Cường Thọ
III. CÁC PHƯƠNG PHÁP PHÂN VÙNG ẢNH
Để phân tích các đối tượng trong ảnh, chúng ta cần phải phân biệt được các
đối tượng cần quan tâm với phần còn lại của ảnh. Những đối tượng này có thể tìm ra
được nhờ các kỹ thuật phân đoạn ảnh, theo nghĩa tách phần tiền cảnh ra khỏi hậu
cảnh trong ảnh. Chúng ta cần phải hiểu được là:
-
Không có kỹ thuật phân đoạn nào là vạn năng, theo nghĩa có thể áp dụng cho
mọi loại ảnh.
-
Không có kỹ thuật phân đoạn nào là hoàn hảo
.
Có thể hiểu phân vùng là tiến trình chia ảnh thành nhiều vùng, mỗi vùng chứa
một đối tượng hay nhóm đối tượng cùng kiểu. Chẳng hạn, một đối tượng có thể là
một kí tự trên một trang văn bản hoặc một đoạn thẳng trong một bản vẽ kỹ thuật
hoặc một nhóm các đối tượng có thể biểu diễn một từ hay hay đoạn thẳng tiếp xúc
nhau. Ta có một số phương pháp phân vùng ảnh như sau:
1. Thuật toán gán nhãn thành phần liên thông
Kỹ thuật này gán cho mỗi thành phần liên thông của ảnh nhị phân một nhãn
riêng biệt. Nhãn thường là các số tự nhiên bắt đầu từ một đến tổng số các thành phần
liên thông có trong ảnh. Giải thuật quét ảnh từ trái sang phải và từ trên xuống dưới.
Trong dòng thứ nhất của các pixel đen, một nhãn duy nhất được gán cho mỗi đường
chạy liên tục của pixel đen. Với mỗi pixel đen của các dòng tiếp theo, các pixel lân
cận trên dòng trước và pixel bên trái được xem xét. Nếu bất kì pixel lân cận nào
được gán nhãn, nhãn tương tự được gán cho pixel đen hiện thời; ngược lại nhãn tiếp
theo chưa được sử dụng được chọn. Thủ tục này được tiếp tục cho tới dòng cuối của
ảnh.
Lúc kết thúc tiến trình này, một thành phần liên thông có thể chứa các pixel
có các nhãn khác nhau vì khi chúng ta xem xét lân cận của pixel đen, chẳng hạn
pixel “?” trong hình vẽ. Pixel đối với lân cận trái và những lân cận trong dòng trước
có thể được gán nhãn một cách riêng biệt. Một tình huống như vậy phải được xác
định và ghi lại. Sau tiến trình quét ảnh, việc gán nhãn được hoàn tất bằng cách thống
nhất các mâu thuẫn các nhãn và gán lại các nhãn chưa sử dụng.
Bài giảng Xử lý ảnh
59
GV. Mai Cường Thọ
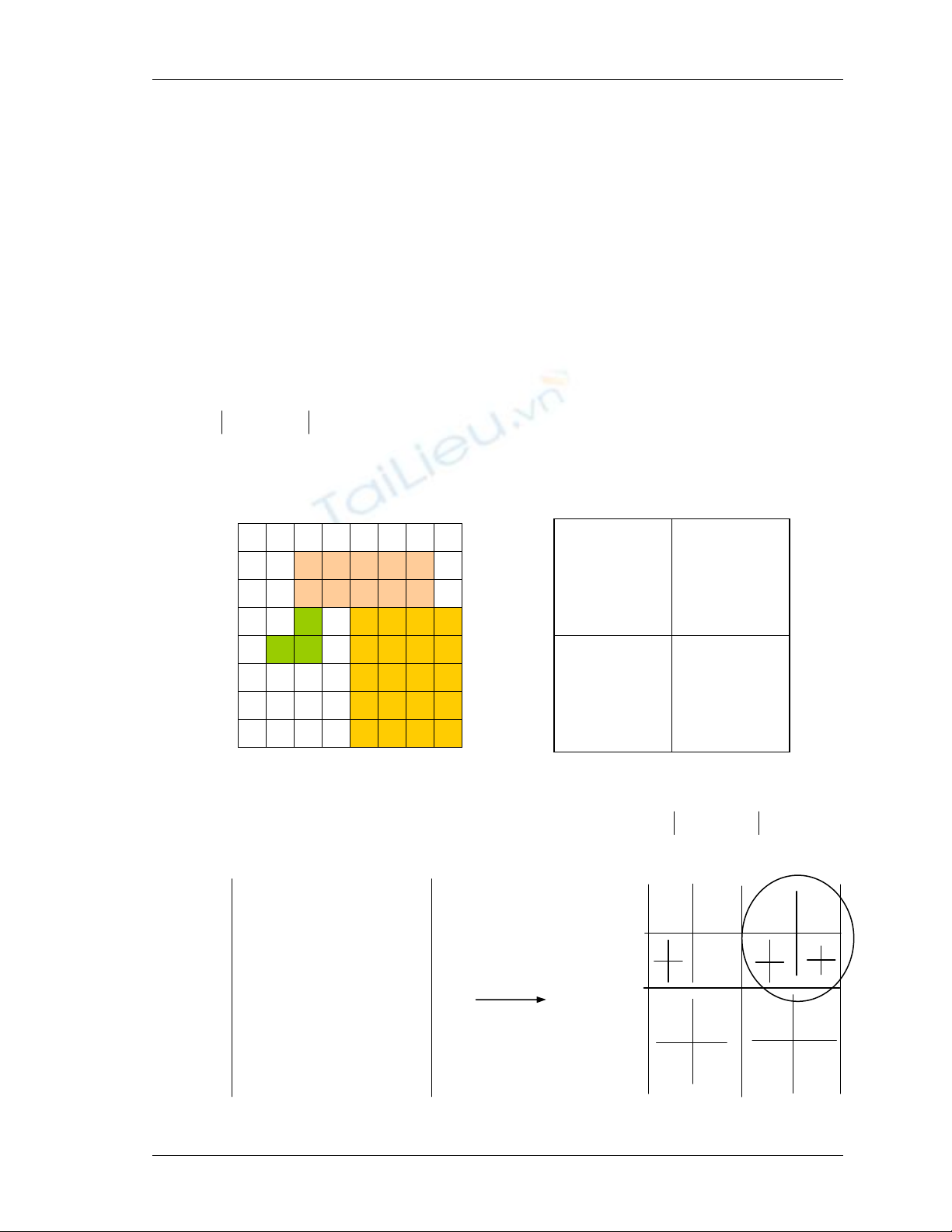
Để minh hoạ ta có hình biểu diễn sau :
Vd : một phương pháp sửa nhãn
∃(p,q) là liên thông 8 mà label(p)<>label(q) -> sửa nhãn cho giống nhau.
2. Phân vùng bằng tách cây tứ phân
Về nguyên tắc, phương pháp này kiểm tra tính hợp thức của tiêu chuẩn một
cách tổng thể trên miền lớn của ảnh. Nếu tiêu chuẩn được thỏa, việc phân đoạn coi
như kết thúc. Trong trường hợp ngược lại, ta chia miền đang xét thành 4 miền nhỏ
hơn. Với mỗi miền nhỏ, ta áp dụng một cách đệ quy phương pháp trên cho đến khi
tất cả các miền đều thỏa.
Thuật toán này tạo nên một cây mà mỗi nút cha có 4 nút con ở mọi mức trừ
mức ngoài cùng. Vì thế cây này có tên là cây tứ phân. Cây này cho ta hình ản rõ nét
về cấu trúc phân cấp của các vùng tương ứng với tiêu chuẩn.
. . . . .
. . . . . . . . .
. . . . . . . . . . . . . .
.
*
*
*
*
. .
*
*
*
. . . . .
1
1
1
1
. .
2
2
2
. . . .
. .
*
*
*
. .
*
*
*
*
. . . . .
1
1
1
. .
2
2
2
2
. . .
.
*
*
*
*
.
*
*
*
*
*
. . . .
1
1
1
1
.
2
2
2
2
2
. . .
. . .
*
*
*
*
*
. . . . . . . . .
1
1
?
*
*
. . . . . .
. . .
*
*
*
*
*
*
.
*
. . . ⇒ . . .
*
*
*
*
*
*
.
*
. . .
*
*
. . . . . . . .
*
*
. .
*
*
. . . . . . . .
*
*
. .
.
*
*
. . . . . . .
*
*
. . .
*
*
. . . . . . .
*
*
. .
.
*
*
. . . . . . . . . . . .
*
*
. . . . . . . . . . .
Hình b . Ảnh ban đầu Hình c . Tiến trình gán nhãn
. . . . . . . . . . . . . .
. . . . . . . . . . . . . .
.
1
1
1
1
. .
2
2
2
. . . . .
1
1
1
1
. .
1
1
1
. . . .
. .
1
1
1
. .
2
2
2
2
. . . . .
1
1
1
. .
1
1
1
1
. . .
.
1
1
1
1
.
2
2
2
2
2
. . . .
1
1
1
1
.
1
1
1
1
1
. . .
. . .
1
1
1
1
1
. . . . . . . . .
1
1
1
1
1
. . . . . .
. . .
1
1
1
1
1
1
.
3
. . . ⇒ . . .
1
1
1
1
1
1
.
2
. . .
4
4
. . . . . . . .
3
3
. .
3
3
. . . . . . . .
2
2
. .
.
4
4
. . . . . . .
3
3
. . .
3
3
. . . . . . .
2
2
. .
.
4
4
. . . . . . . . . . . .
3
3
. . . . . . . . . . .
Hình d . Sau khi quét đầy đủ Hình e .Kết quả sau cùng
. . . . . . . . . ……..
. . . . P P P P . . . .
. . . . L ? . . . . . . .
. . . . . . . .. . . . . ..
P: lân cận trước, L lân cân trái
Bài giảng Xử lý ảnh
60
GV. Mai Cường Thọ
Một vùng thỏa chuẩn sẽ tạo nên một nút lá, nếu không nó sẽ tạo nên một nút
trong và có 4 nút con tương ứng với việc chia làm 4 vùng. Ta cứ tiếp tục như vậy
cho đến khi phân xong. Các nút của cây biểu diễn số vùng đã phân.
Tiêu chuẩn phân vùng ở đây là màu sắc. Nếu mọi điểm của vùng đều là màu
trắng thì sẽ tạo nên nút lá trắng và tương tự như vậy với nút lá đen. Nút màu ghi
vùng không thuần nhất và phải tiếp tục chia.
Với ngưỡng θ cho trước, vùng thuần nhất phải thỏa điều kiện
•
Độ lệch chuẩn σ < θ
•
Hoặc
θ<−
MinMax
với Max, Min lần lượt là giá trị lớn nhất và nhỏ nhất của
mức xám trong vùng cần chia.
•
Giá trị điểm ảnh trong vùng bằng cách lấy trung bình giá trị của vùng đó
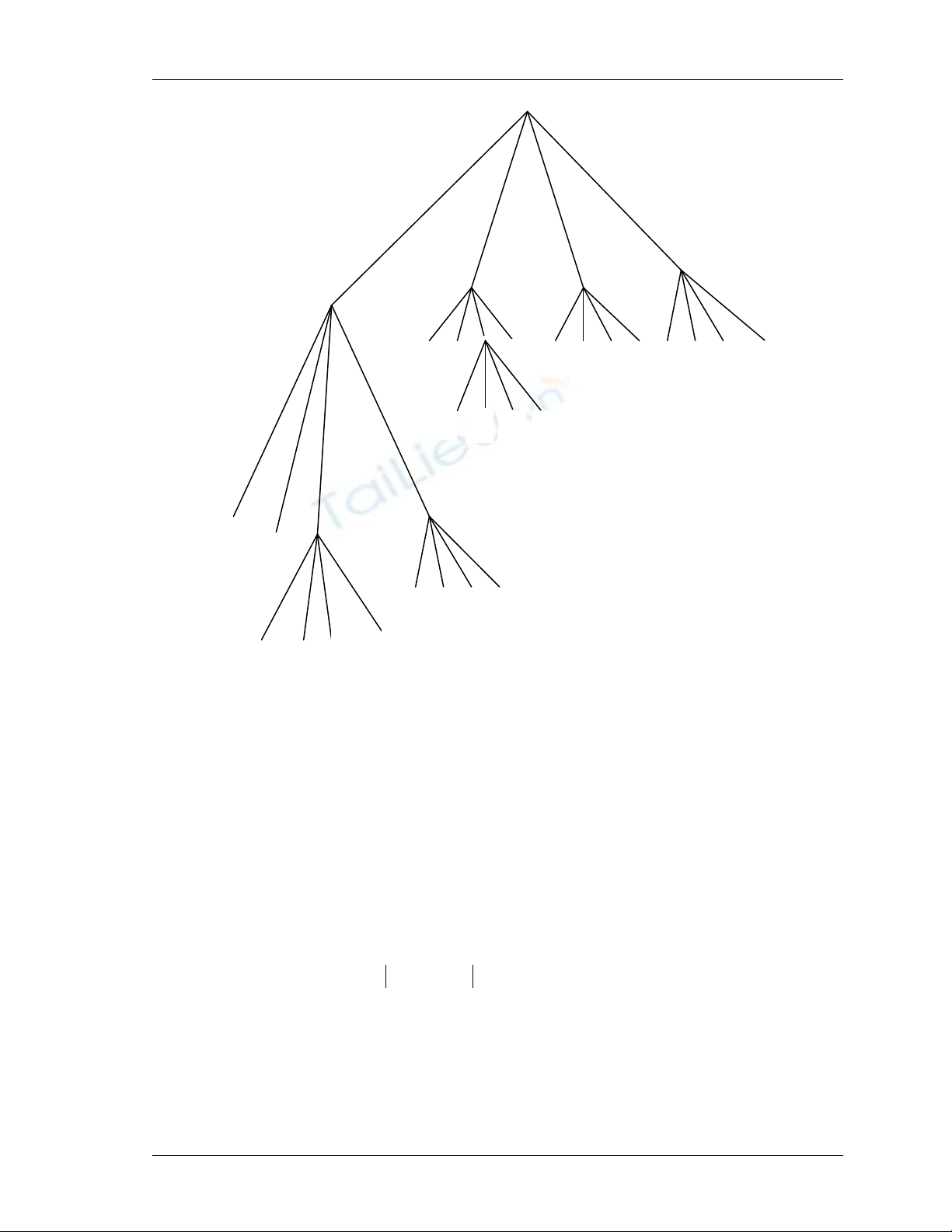
Ảnh gốc Phân đoạn ở mức 1
Ví dụ:
Cho ảnh S(m, n) , hãy phân vùng theo tiêu chí: ngưỡng θ= 2 và
θ<−
MinMax
98664422
98664422
22335577
22335577
12335578
98765532
88664422
88664422
),( =nmS
kết quả
Vùng 2
Vùng 1
Vùng 3
Vùng 4
98664422
98664422
22335577
22335577
12335578
98765532
88664422
88664422
),( =nmS
Vùng 1
Bài giảng Xử lý ảnh
61
GV. Mai Cường Thọ
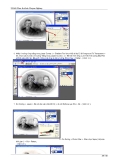
Ta có cây tứ phân như sau
3. Phân vùng bởi hợp
Ý tưởng của phương pháp này là xem xét ảnh từ các miền nhỏ nhất rồi hợp
chúng lại nếu thỏa tiêu chuẩn để được một miền đồng nhất lớn hơn. Ta lại tiếp tục
với miền thu được cho tới khi không thể hợp được nữa. Số miền còn lại cho ta kết
quả phân đoạn. Như vậy miền nhỏ nhất của bước xuất phát là điểm ảnh.
Phương pháp hợp vùng được thực hiện như sau:
•
Giả sử có 2 vùng ω và ω
’
•
Ta xác định cặp các điểm 4 láng giềng (p, q) sao cho p ∈ω và q ∈ω
’
•
Xác định
≤−
=otherwise
qIpIif
qpT 0
)()(1
),(
1
θ
Trong đó I(p), I(q) là giá trị mức xám của điểm p và q, θ
1
là giá trị ngưỡng cho
trước.
•
Gọi b(ω) và b(ω
’
) là số điểm biên của 2 vùng ω và ω
’
(8)
(3)
22
21
(1)
(2)
(8)
(9)
14
4
3
2
1
13
12
11
(6)
(7)
(6)
(3)
(3)
23
24
(4)
(2)
(5)
(2)
(8)
(7)
(5)
(7)
(2)
(4)
(2)
(3)
(6)
(9)