Bài giảng học Đại lượng ngẫu nhiên

Chia sẻ: Lâm Trúc | Ngày: | Loại File: PDF | Số trang:58

Thêm vào BST

Báo xấu

133
lượt xem 16
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

X Chỉ nhận một số hửu hạn các giá trị, hoặc một số vô hạn đếm được các giá trị. 1.2.ĐLNN LIÊN TỤC . Tập hợp các giá trị mà X nhận lấp đầy một khoảng của trục số hoặc toàn bộ trục số. . X là ĐLNN liên tục thì xác suất tại một điểm bằng 0 P(X=a)=0.Toán học là môn khoa học nghiên cứu về các số, cấu trúc, không gian và các phép biến đổi. Nói một cách khác, người ta cho rằng đó là môn học về "hình và số." Theo quan điểm chính thống, nó...

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng học Đại lượng ngẫu nhiên

C.2 ÑAÏI LÖÔÏNG NGAÃUNHIEÂN 1.KHAÙI NIEÄM 2.ÑLNN RÔØI RAÏC-ÑLNN LIEÂN TUÏC 3.CAÙC THAM SOÁ ÑAËC TRÖNG 4.CAÙC QUY LUAÄT PHAÂN PHOÁI
1.KHAÙI NIEÄM ÑLNN. 1.1.ÑLNN RÔØI RAÏC . X Chæ nhaän moät soá höûu haïn caùc giaù trò, hoaëc moät soá voâ haïïn ñeám ñöôïc caùc giaù trò. 1.2.ÑLNN LIEÂN TUÏC . Taäp hôïp caùc giaù trò maø X nhaän laáp ñaày moät khoaûng cuûa truïc soá hoaëc toaøn boä truïc soá. . X laø ÑLNN lieân tuïïc thì xaùc suaát taïi moät ñieåm baèng 0 P(X=a)=0
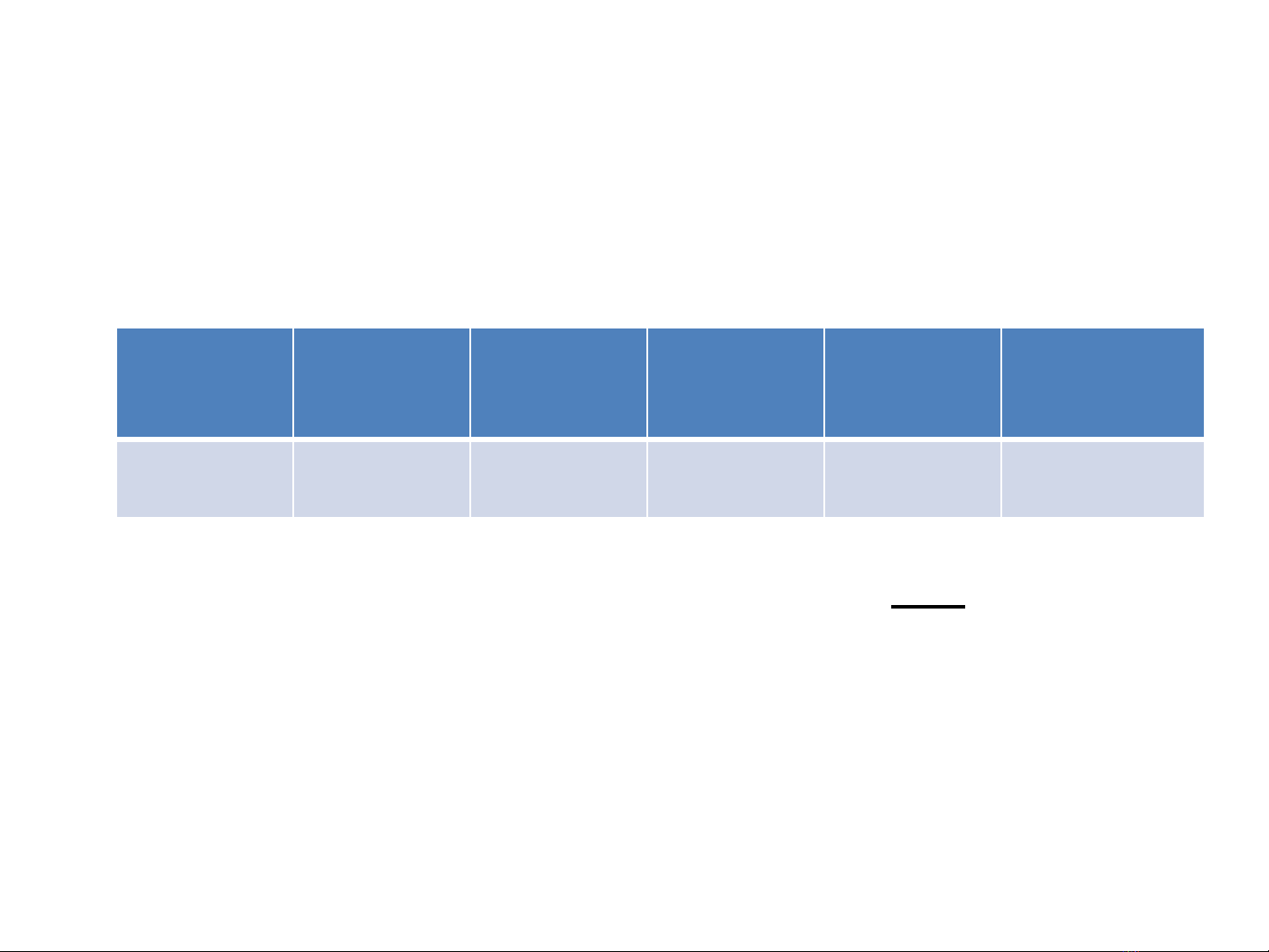
2.QUY LUAÄT PHAÂN PHOÁI XAÙC SUAÁT CUÛA ÑLNN. 2.1.BAÛNG PHAÂN PHOÁI XAÙC SUAÁT. … ... xn x2 x1 X … … p1 p2 pn P Vôùi: P( X = xi ) = pi ; i = 1, n n ∑ p = 1; p ≥ 0 i i i =1
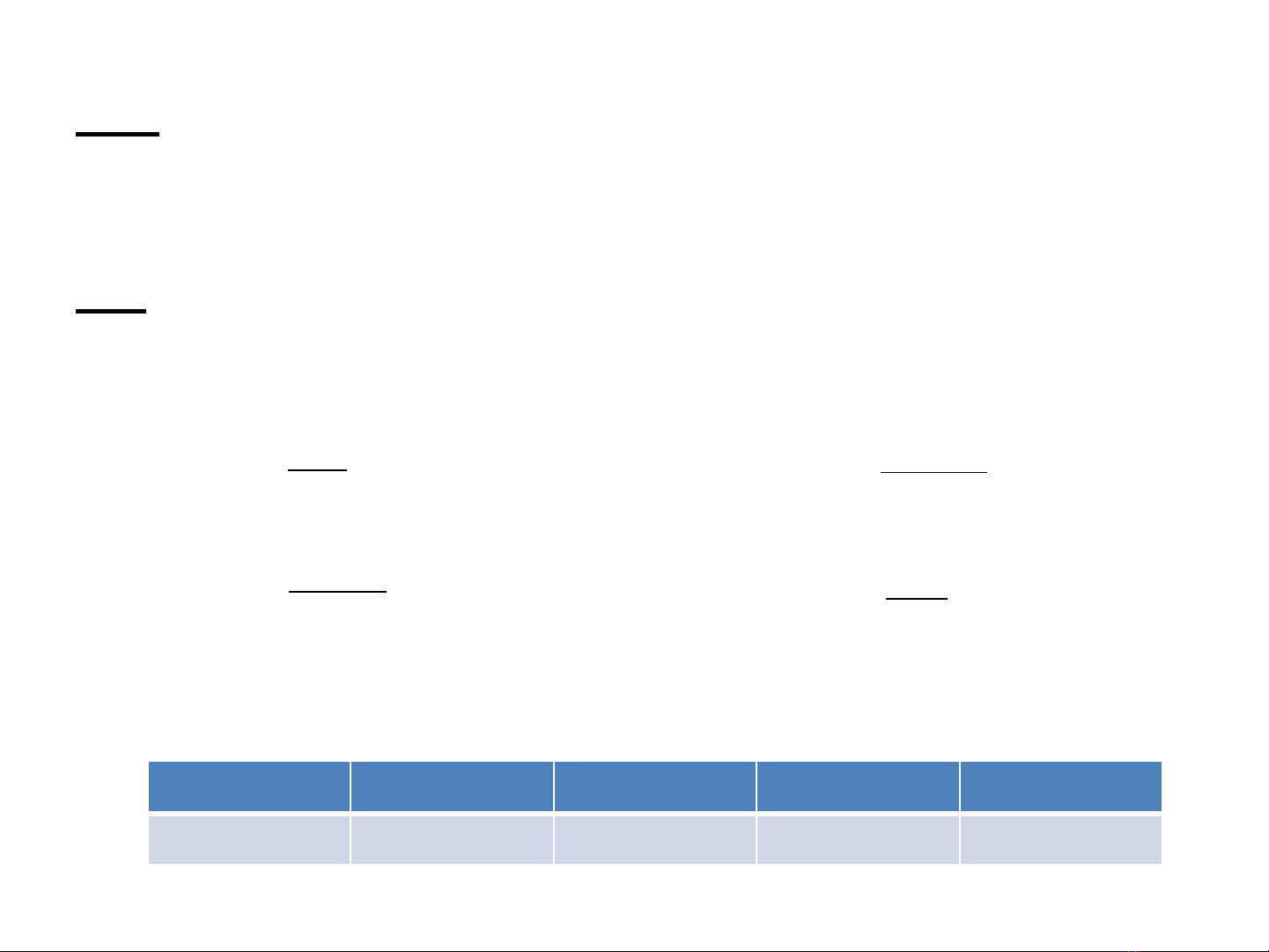
VD: Moät loâ haøng coù 25 sp toát, 5 sp xaáu. Moät ngöôøi mua 3 sp, goïi X laø soá sp toát trong 3 sp mua, laäp baûng phaân phoái xaùc suaát cuûa X NX: X laø moät ÑLNN rôøi raïc, X nhaän caùc giaù trò: 0, 1, 2, 3. 3 C25C52 1 C5 P( X = 0) = 3 = 0,002463 P( X = 1) = = 0,061576 3 C30 C30 2 1 3 C25C5 C25 P( X = 2) = = 0,369458 P( X = 3) = 3 = 0,566503 3 C30 C30 Baûng phaân phoái xs cuûa X: X 0 1 2 3 P 0,002463 0,061576 0,369458 0,566503
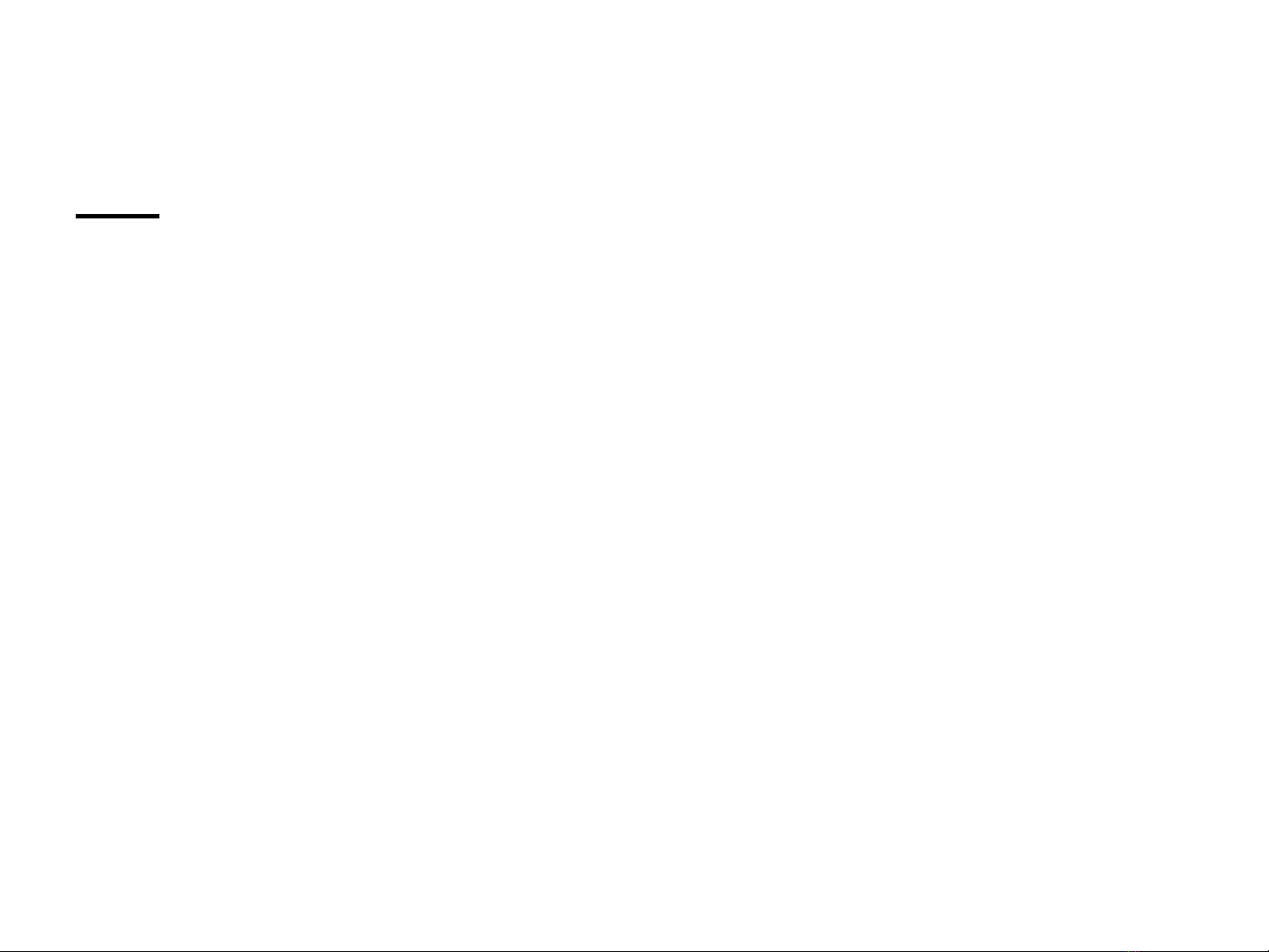
VD: Moät troø chôi: Tung moät con xuùc xaéc 3 laàn. Neáu xuaát hieän 3 maët 1 ñöôïc 100 ngaøn ñoàng. Neáu xuaát hieän 2 maët 1 ñöôïc 50 ngaøn ñ. Neáu xuaát hieän 1 maët 1 ñöôïc 10 ngaøn ñ. Neáu khoâng coù maët 1 xuaát hieän thì maát 20 ngaøn ñ. Goïïi X laø soá tieàn ñöôïc thua trong troø chôi treân. Tìm quy luaät phaân phoái xaùc suaát cuûa X.
X nhaän caùc giaù trò: -20, 10, 50, 100 15 1 P( X = 50) = P( X = 100) = 216 216 125 75 P( X = −20) = P( X = 10) = 216 216 Quy luaät phaân phoái xaùc suaát cuûa X laø: X -20 10 50 100 P 125/216 75/216 15/216 1/216
2.2.HAØM PHAÂN PHOÁI XAÙC SUAÁT CUÛA ÑLNN RÔØI RAÏC. ÑN: Haøm phaân phoái xaùc suaát cuûa ÑLNN X laø: F ( x) = P( X < x) Neáu X laø ÑLNN rôøi raïc thì haøm phaân phoái xaùc suaát laø: F ( x) = P( X < x) = ∑ P( X = xi ) xi < x
VD: X laø ÑLNN rôøi raïc coù baûng phaân phoái xaùc suaát laø: X 1 3 5 8 10 P 0,2 0,1 0,3 0,3 0,1 Haøm phaân phoái XS cuûa X laø: F ( x) = P( X < x) = ∑ P( X = xi ) xi < x x ≤1 0 0,2 1< x ≤ 3  3< x ≤5 0,3 F ( x) =   5< x≤8 0,6 0,9 8 < x ≤ 10  1 10 < x 
2.3.HAØM MAÄT ÑOÄ XAÙC SUAÁT. Haøm soá f(x) xaùc ñònh treân toaøn truïc soá, ñöôïc goïi laø haøm maät ñoä cuûa ÑLNN lieân tuïc X neáu: i ) f ( x) ≥ 0; ∀x ∈ R +∞ ii ) ∫ f ( x)dx = 1 −∞ b iii ) P(a < X < b) = ∫ f ( x)dx a CHUÙ YÙ:X laø ÑLNN lieân tuïc thì: P ( X = a ) = P ( X = b) = 0 P ( a < X < b) = P ( a ≤ X < b) = P ( a < X ≤ b) = P ( a ≤ X ≤ b)
VD: Cho X laø ÑLNN lieân tuïc coù haøm maät ñoä laø: 1  ; x ∈ [0,2] f ( x) =  2 0; x ∉ [0,2]  Kieåm chöùng: . f ( x) ≥ 0∀x ∈ R +∞ 2 1 . ∫ f ( x)dx = ∫ dx = 1 2 −∞ 0
VD: Cho X laø ÑLNN lieân tuïc coù haøm maät ñoä laø: ax ; x ∈ [1,3] 2 f ( x) =  0; x ∉ [1,3] a) Tìm a. b) Tính P(2
2.4.HAØM PHAÂN PHOÁI CUÛA ÑLNN LIEÂN TUÏC. Neáu X laø ÑLNN lieân tuïc coù haøm maät ñoä laø f(x) thì haøm phaân phoái xaùc suaát cuûa ÑLNN lieân tuïc X laø: x ∫ F ( x) = f (t )dt −∞ CHUÙ YÙ: Neáu F(x) laø haøm phaân phoái xaùc suaát cuûa ÑLNN lieân tuïc X, thì haøm maät ñoä laø: f ( x) = F ( x) ,
VD: X laø ÑLNN lieân tuïc coù haøm maät ñoä laø: 1; x ∈ [0,1] f ( x) =  0; x ∉ [0,1] thì haøm phaân phoái xaùc suaát cuûa X laø: 0; x < 0  F ( x) =  x;0 ≤ x ≤ 1 1; x > 1 
TÍNH CHAÁT CUÛA HAØM PHAÂN PHOÁI: 0 ≤ F ( x) ≤ 1; ∀x ∈ R i) ii) F(x) laø haøm khoâng giaûm x1 < x2 ⇒ F ( x1 ) ≤ F ( x2 ) iii) lim F ( x) = 1 x → +∞ lim F ( x) = 0 x → −∞ iv) Neáu X laø ÑLNN lieân tuïc thì F(x) laø haøm lieân tuïc
3.CAÙC THAM SOÁ ÑAËC TRÖNG CUÛA ÑLNN 3.1.KYØ VOÏNG .X laø ÑLNN rôøi raïc n µ = E ( X ) = ∑ xi pi i =1 .X laø ÑLNN lieân tuïc +∞ µ = E ( X ) = ∫ x. f ( x)dx −∞ Tính chaát kyø voïng i) E(C)=C (C: haèng soá) ii) E(CX)=CE(X) iii) E(X+Y)=E(X)+E(Y) iv) E(X.Y)=E(X).E(Y) neáu X, Y ñoäc laäp
VD: Thu nhaäp cuûa 100 CN cuûa moät XN. X(trieäu ñ) 1,2 1,5 2,0 2,5 Soá CN 20 40 30 10 Tính thu nhaäp trung bình cuûa 100 CN GIAÛI: Baûng phaân phoái xaùc suaát: X 1,2 1,5 2,0 2,5 P 0,20 0,40 0,30 0,10 E(X)=thu nhaäp trung bình cuûa 100 CN= 4 ∑x p = 1,2(0,2) + 1,5(0,4) + 2(0,3) + 2,5(0,1) = 1,69 i i i =1
VD: X(phuùt) laø thôøi gian chôø ñeøn ñoû taïi moät ngaõ tö,laø moät ÑLNN lieân tuïc coù haøm maät ñoä laø: 4 3  x ; x ∈ [0,3] f ( x) =  81 0; x ∉ [0,3]  a)Tính thôøi gian chôø ñôïi trung bình b) Tính xaùc suaát phaûi chôø töø 1 ñeán 2 ph GIAÛI: a) E(X)= +∞ 3 4 12 ∫ x. f ( x)dx = 81 ∫ x dx = 4 5 b) −∞ 0 2 2 4 15 P(1 ≤ X ≤ 2) = ∫ f ( x)dx = ∫ x dx = 3 81 1 81 1
3.2.PHÖÔNG SAI .X laø ÑLNN rôøi raïc n σ = VAR( X ) = ∑ [ xi − E ( X )] . pi 2 2 X i =1 .X laø ÑLNN lieân tuïc +∞ σ = VAR( X ) = ∫ [ x − E ( X )] . f ( x)dx 2 2 X −∞
CHUÙ YÙ: .X ÑLNN rôøi raïc σ = VAR( X ) = E ( X ) − [ E ( X )] 2 2 2 X n E ( X ) = ∑ x . pi 2 2 i i =1
.TÍNH CHAÁT CUÛA PHÖÔNG SAI i )Var (C ) = 0 ii )Var (CX ) = C Var ( X ) 2 iii )Var ( X + C ) = Var ( X ) iv)Var ( X + Y ) = Var ( X ) + Var (Y ) neáu X,Y ñoäc laäp