
Chương 4. Cơ sở lý thuyết mẫu
Khái niện phương pháp mẫu
Tổng thể nghiên cứu
Mẫu ngẫu nhiên
Thống kê đặc trưng mẫu
Quy luật phân phối xác suất của một số thống kê
đặc trưng mẫu
Suy diễn thống kê
1
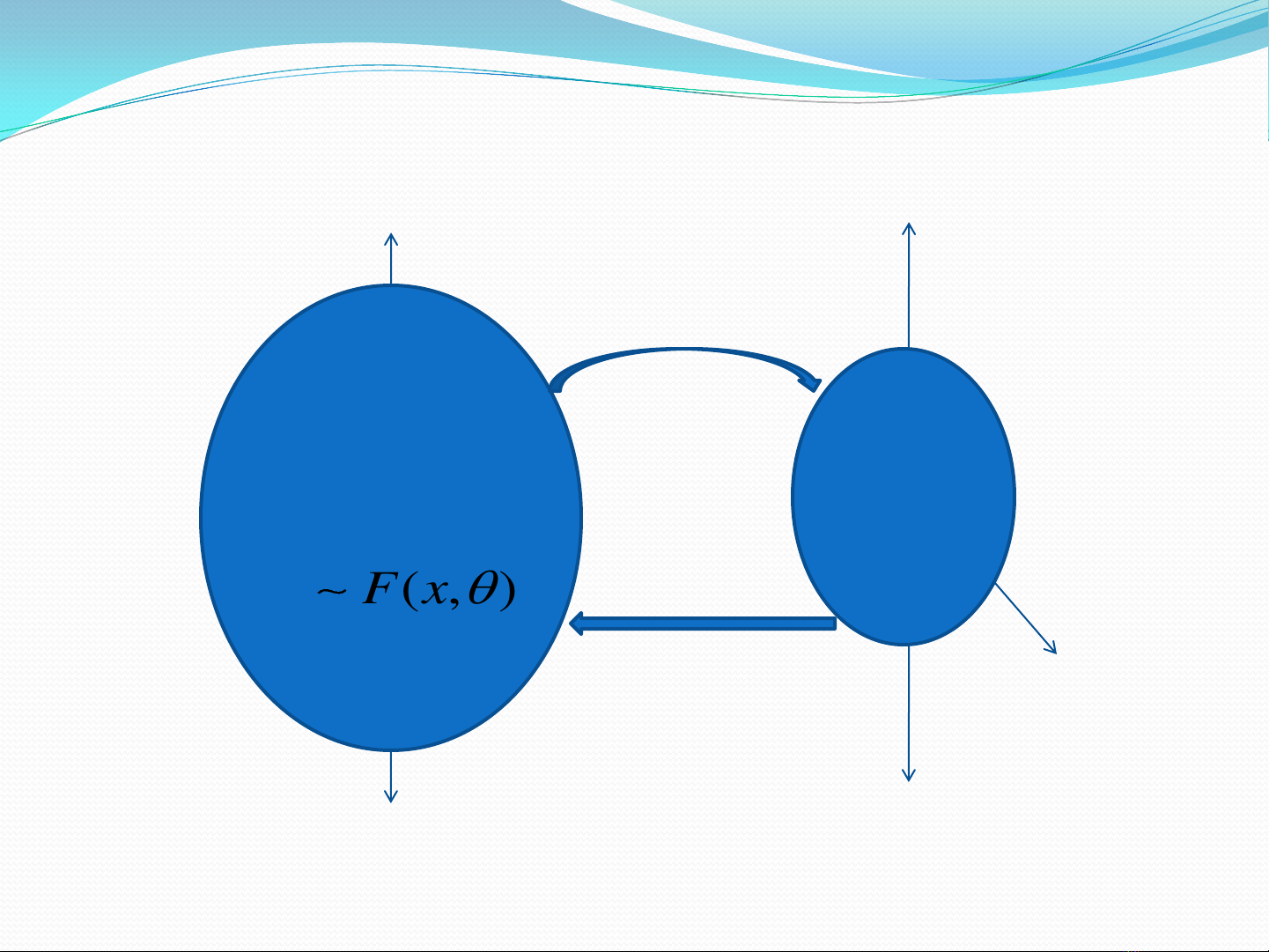
4.1. Khái niệm phương pháp mẫu
2
Dấu hiệu
Phương pháp mô tả
Tổng
thể
(N)
Phương pháp mô tả số liệu
Tham số đặc trưng Thống kê đặc trưng
Mẫu
ngẫu
nhiên
Phương
pháp
chọn
mẫu
( , )X F x
1
( ,..., )
nn
W X X

4.2. Tổng thể nghiên cứu
Mô tả tổng thể
Biến ngẫu nhiên Xlàm đại diện và để lượng hóa cho
dấu hiệu nghiên cứu χcủa tổng thể được gọi là biến
ngẫu nhiên gốc, quy luật phân phối xác suất của nó gọi
là quy luật phân phối gốc.
Bản chất.Biến ngẫu nhiên gốc có thể là rời rạc hoặc
liên tục.
3

Giả sử,tổng thể có kích thước là N,dấu hiệu
nghiên cứu χ nhận các giá trị là:x1, x2,…, xn.
Trung bình tổng thể:
Phương sai tổng thể:
Phương sai tổng thể tính bằng:
4
N k k
i i i i i
i 1 i 1 i 1
11
m x N x p x E(X)
NN
Nk
2 2 2
i i i
i 1 i 1
11
(x m) N (x m)
NN
k2
2 2 2 2
ii
i1
1N x m E(X ) E(X)
N
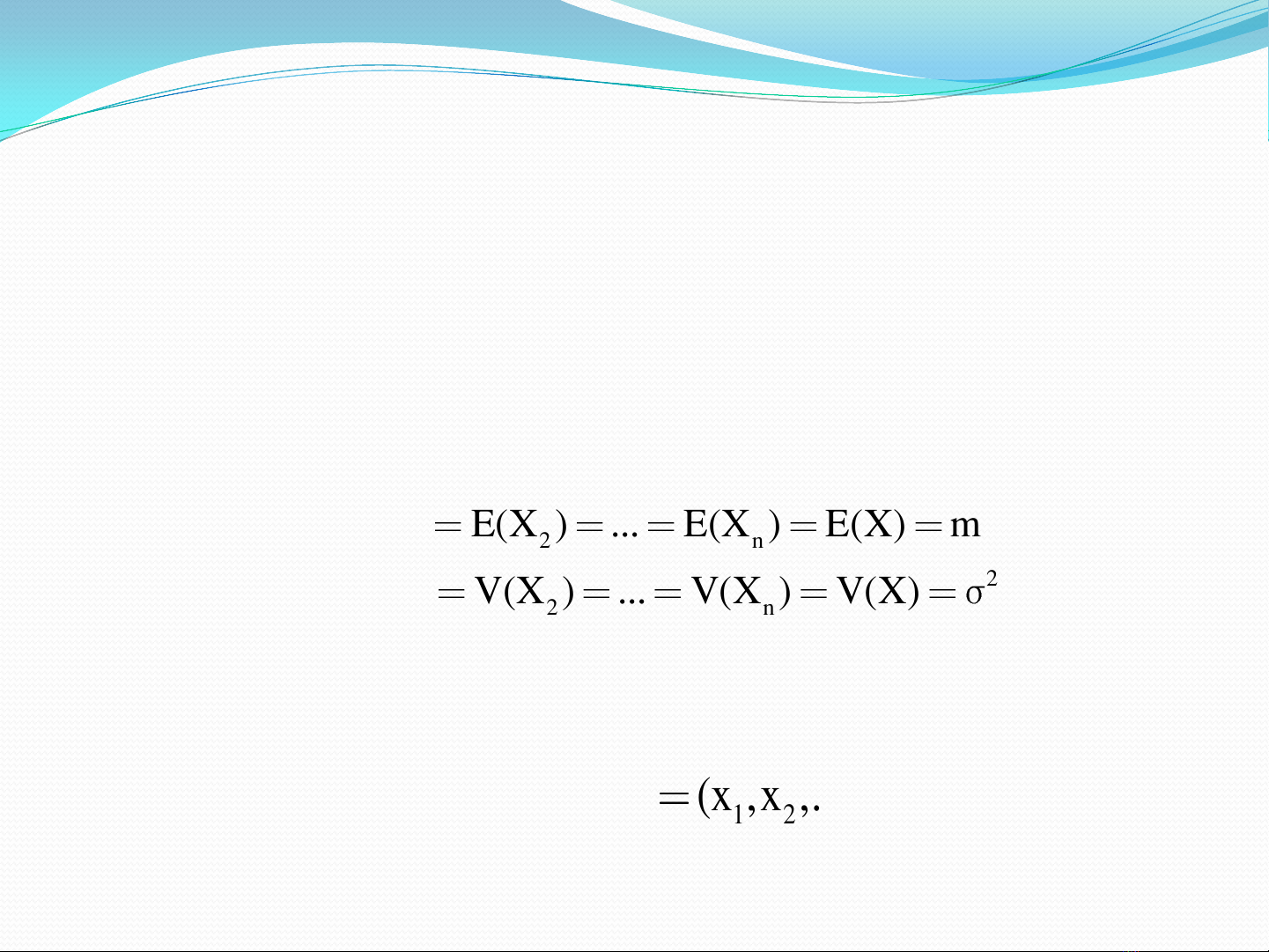
4.3. Mẫu ngẫu nhiên
Tập hợp của nbiến ngẫu nhiên độc lập X1, X2,…, Xn
được thành lập từ biến ngẫu nhiên gốc Xtrong tổng
thể nghiên cứu được gọi là mẫu ngẫu nhiên kích
thước n, ký hiệu: Wn=(X1, X2,…, Xn).
Tính chất
Khi thực hiện phép thử trên mẫu ngẫu nhiên W, ta
thu được các giá trị x1,x2,…,xn.Tập hợp (x1, x2,…,xn)là
một mẫu cụ thể,ký hiệu:
5
1 2 n
2
1 2 n
E(X ) E(X ) ... E(X ) E(X) m
V(X ) V(X ) ... V(X ) V(X)
1 2 n
w (x ,x ,...,x )


























