B MÔN TOÁN NG D NG - ĐHBKỘ Ứ Ụ
-------------------------------------------------------------------------------------
TOÁN 1 HK1 0708
•BÀI 2: HÀM S (SV)Ố
•TS. NGUY N QU C LÂN (09/2007)Ễ Ố
N I DUNGỘ
---------------------------------------------------------------------------------------------------------------------------------
1- KHÁI NI M HÀM SỆ Ố
2- CÁC CÁCH XÁC ĐNH HÀM SỊ Ố
3- NH C L I: HÀM CẮ Ạ Ơ B N (PH THÔNG)Ả Ổ
4- HÀM S NGỐ Ư CỢ
5- HÀM LƯNG GIÁC NGỢ Ư CỢ
6- HÀM HYPERBOLIC
7- ÁP D NG K THU TỤ Ỹ Ậ
KHÁI NI M HÀM S Ệ Ố
-----------------------------------------------------------------------------------------------------------------------------------
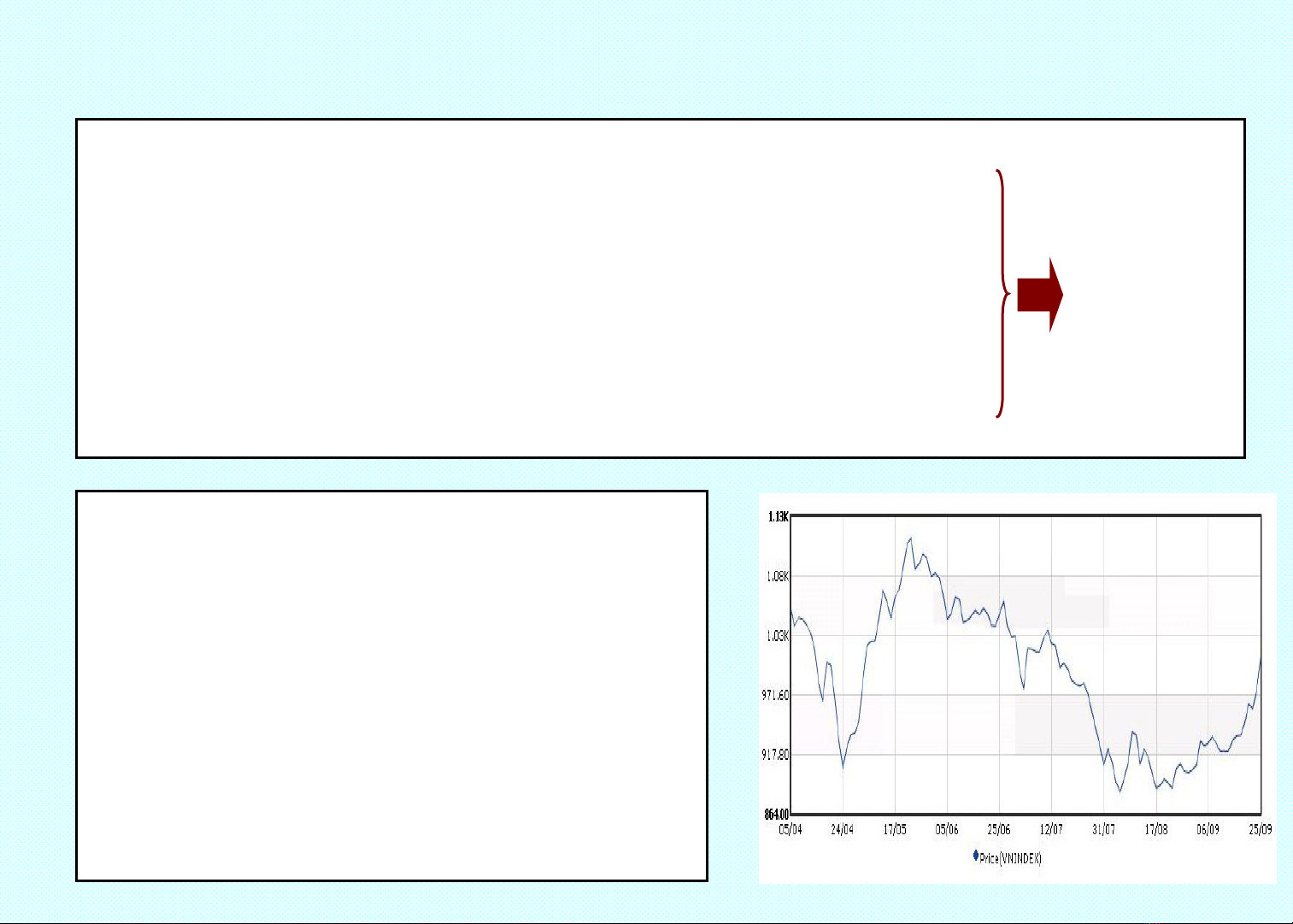
VD: Đ th VNINDEX (ch ng ồ ị ứ
khoán) Hàm s : giá ch ng ố ứ
khoán theo ??? (Th i gian? ờ
Giá vàng? Bi n ếđng chính ộ
tr ? & Bi u th c y = ???ị ể ứ
Đi lạ ư ng A bi n thiên ph thu c ợ ế ụ ộ đi lạ ư ng B:ợ
Đi s ng: Ti n ờ ố ề đi n theo s kwh tiêu th , giá ệ ố ụ
vàng trong nưc theo th gi i …ớ ế ớ
K thu t: T a ỹ ậ ọ đ ch t ộ ấ đi m theo th i gian … ể ờ
Tương
quan
hàm số
L CH S Ị Ử
-----------------------------------------------------------------------------------------------------------------------------------
Gi a TK 18, Euler: Bi u di n ữ ể ễ
hàm s qua ký t ố ự y = f(x)
1786, Scotland:
The Commercial
an Political Atlas,
Playfair. Đ th ồ ị
so sánh xu t & ấ
nh p kh u t ậ ẩ ừ
Anh sang Đan
M ch + Na Uyạ
x :Vaøo
f :Haøm
tính Maùy
y :Ra
ĐNH NGHĨA TOÁN H C Ị Ọ
-----------------------------------------------------------------------------------------------------------------------------------
MXĐ Df = {x| f(x) có nghĩa}
RX
RY
Hàm s y = f(x): X ố R Y R:
Quy lu t tậ ương ngứ x X y Y.
Bi n s x, giá tr y. ế ố ị Tương quan hàm
số: 1 giá tr x cho ra 1 giá tr yị ị
M t x ộ Nhi u y: K0 ph i ề ả
hàm nghĩa thông thưng ờ
(Nhưng hàm đa tr ?)ị
MGTr Imf: ịy =f(x), xDf y = sinx D= R, Imf = [–1, 1]