Ph
Ph
n 2
n 2
To
Toá
án t
n t
Laplace
Laplace
Phép bin ñi Lapalace
Phép bin ñi Lapalace ngưc
ng dng bin ñi Lapace vào PT vi phân
ng dng bin ñi Lapace vào Gii tích Mch ñin
Bài ging Toán KThut 2012 1
Chương
Chương 3 Ph
3 Phé
ép bi
p bi
n ñ
n ñ
i Laplace
i Laplace
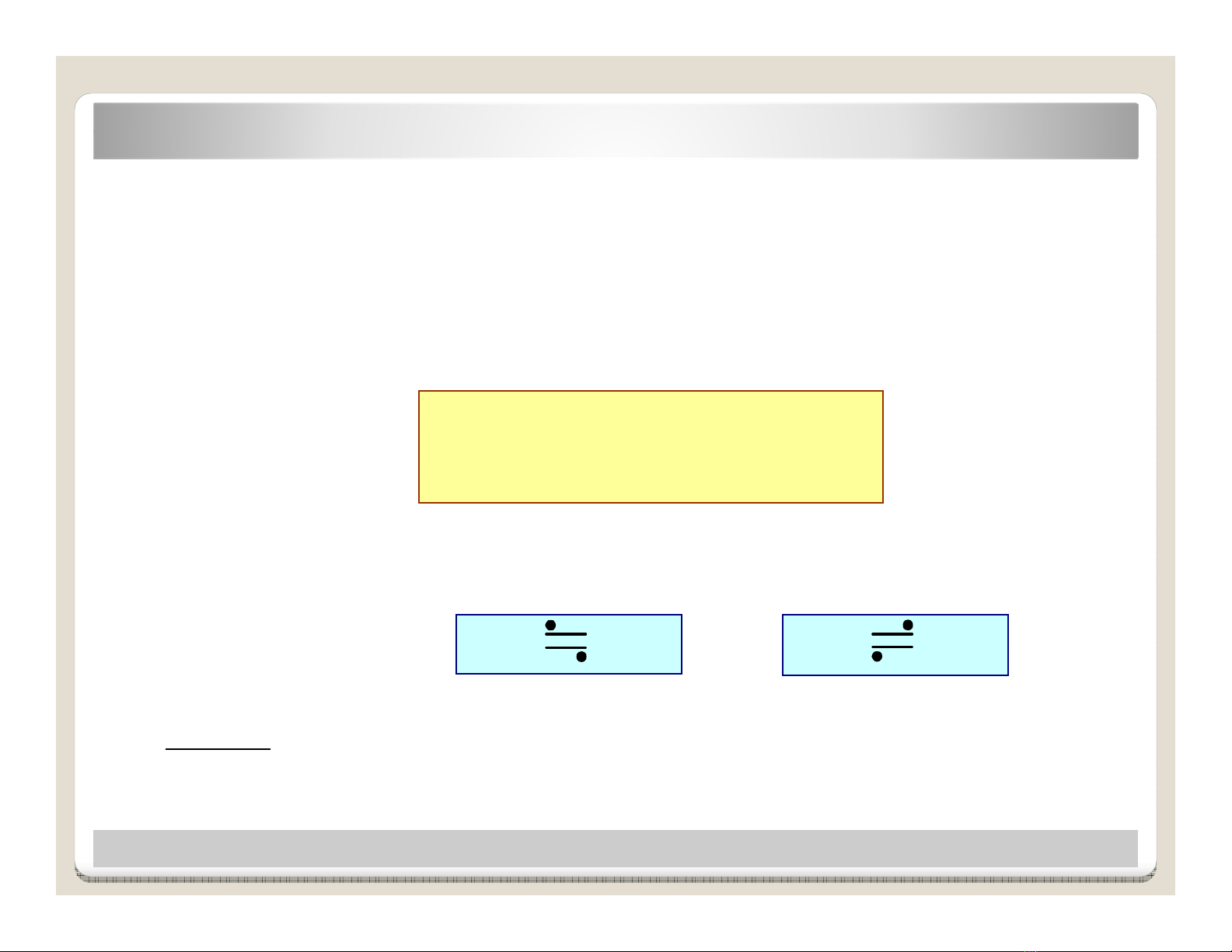
ðnh nghĩa
F(s) : nh Laplace
f(t) : gc
Ký hiu khác hay
Lưu ý trong phm vi giáo trình ta chxét các giá trs trong
khong tích phân là hi t
Bài ging Toán KThut 2012 2
{ }
0
( ) ( ) ( ) st
F s f t f t e dt
−
+∞
−
= = ∫
f(t) là hàm (có thphc) ca bin sthc t (t ≥0) sao cho
tích phân hi tít nht vi mt sphc s = a + jb
nh ca hàm f(t) qua bin ñi Laplace là hàm F(s) ñưc
ñnh nghĩa
( ) ( )
F s f t
( ) ( )
f t F s
T
Tí
ính ch
nh ch
t h
t hà
àm g
m g
c f(t)
c f(t)
Tp hp các hàm f(t) ca bin sthc t sao cho tích phân hi tít
nht vi mt sphc s gi là lp hàm gc.
Trong ñó tp hp các giá trca s sao cho tích phân tn ti thì ñưc
gi là min hi t(hay min qui t).
Ta có thchng minh ñưc lp các hàm gc phi tha mãn các tính
cht sau.
f(t) = 0, vi mi t < 0.
Khi t ≥0, hàm f(t) liên tc cùng vi các ño hàm cp ñ ln trên toàn trc t,
trmt shu hn ñim gián ñon loi mt.
Khi t→∞hàm f(t) có cp tăng bchn, tc là tn ti hng ss>0 và M>0 sao
cho Khi ñó so= inf ; {s} ñưc gi là ch s tăng ca
hàm f. (Tc là hàm f(t) không ñưc tăng nhanh hơn hàm est ñ ñm bo tích
phân Laplace hi t).
Bài ging Toán KThut 2012 3
( ) ; 0
st
≤ ∀ >
Lưu ý trong phm vi giáo trình ta chxét các giá trs trong
khong tích phân là hi t
Bi
Bi
n ñ
n ñ
i Laplace c
i Laplace c
a m
a m
t s
t s
h
hà
àm thông d
m thông d
ng
ng
Bài ging Toán KThut 2012 4
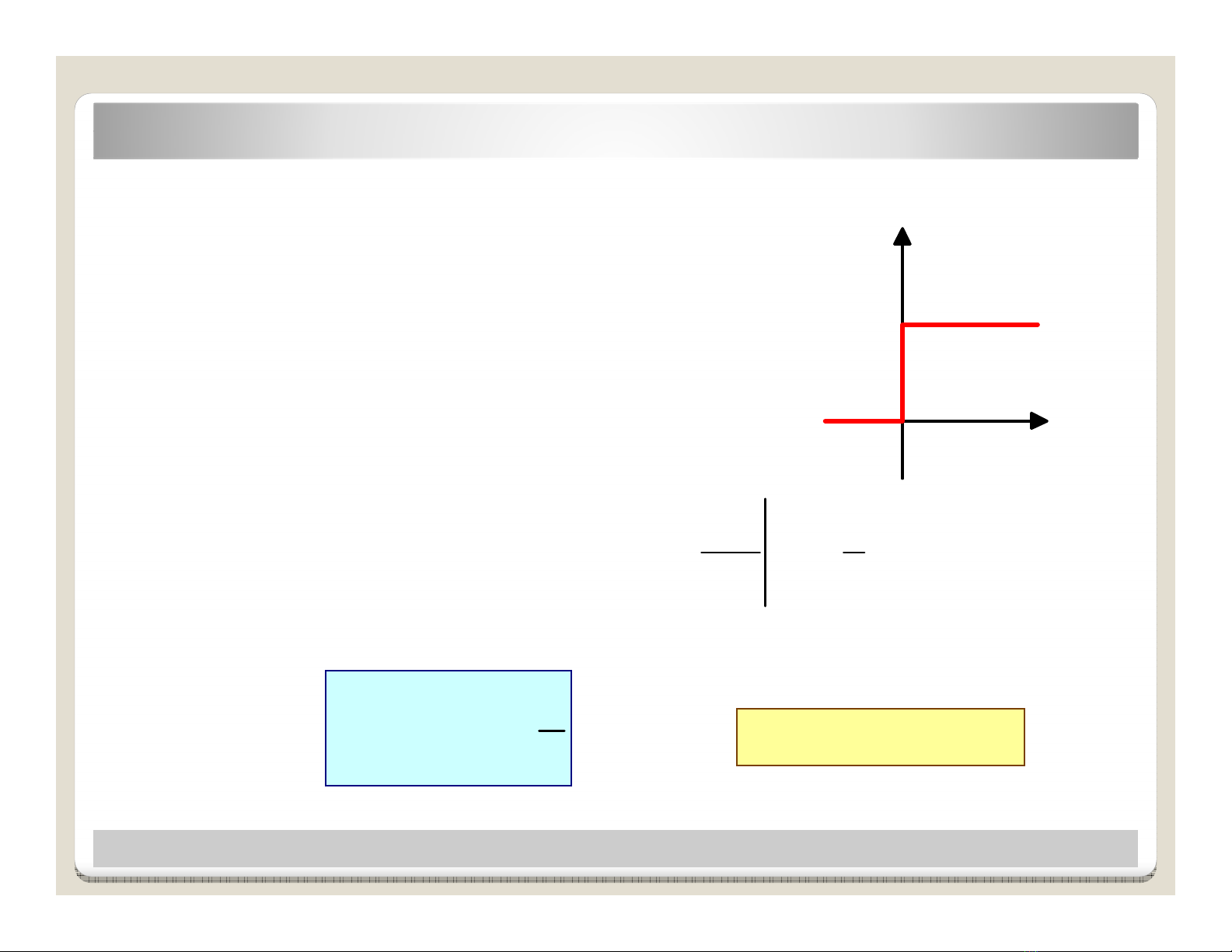
Hàm bưc (nc) ñơn v : u(t)
0 0
( )
1 0
t
u t
t
<
=
>
t
( )
u t
1
0
0
0
1
( ) ( )
st
st st e
F s u t e dt e dt
s s
−
+∞
+∞ +∞ −
− −
= = = =
−
∫ ∫
{ }
1
( )u t
s
=
Mi'n hi tS > 0
Bi
Bi
n ñ
n ñ
i Laplace c
i Laplace c
a m
a m
t s
t s
h
hà
àm thông d
m thông d
ng
ng
Bài ging Toán KThut 2012 5
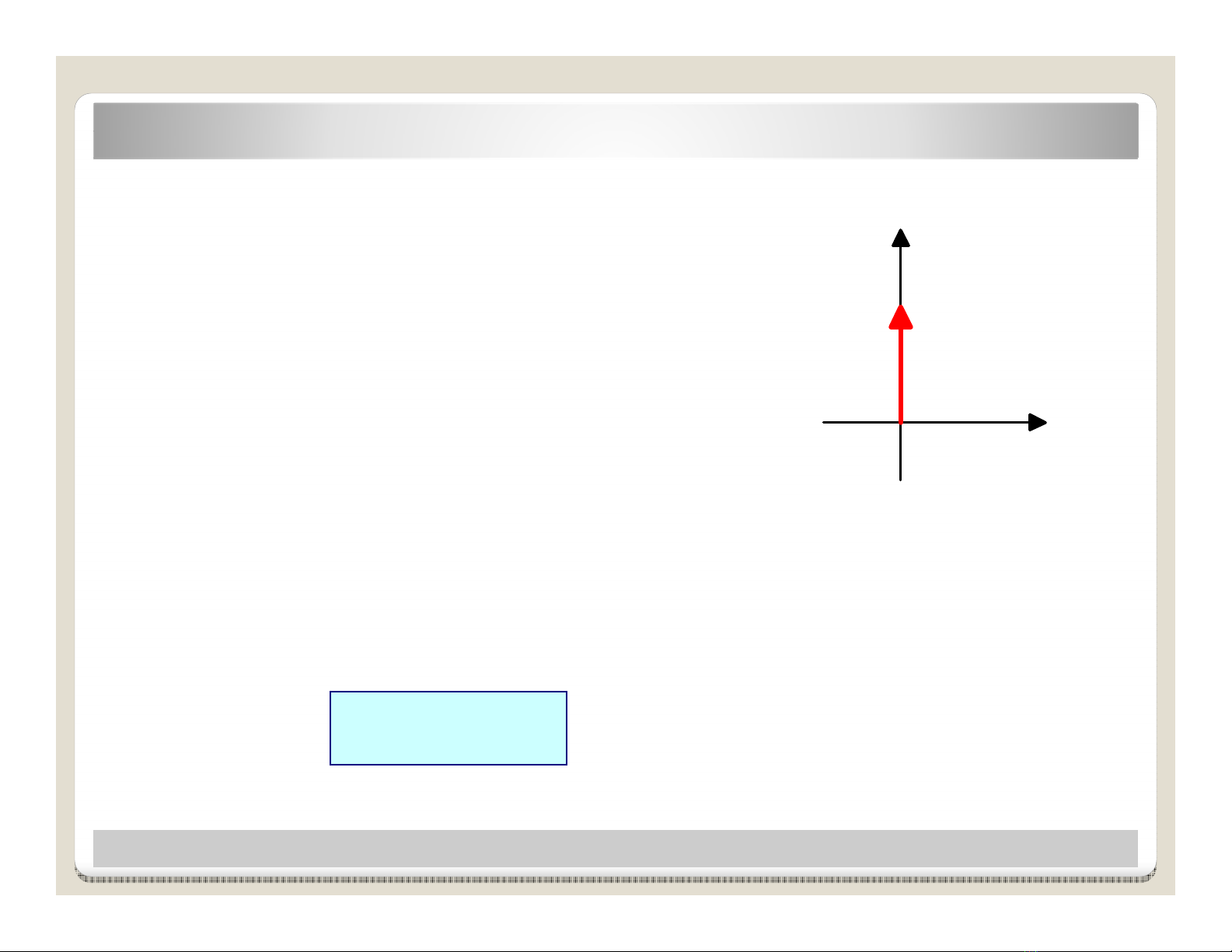
Hàm dirac :
δ
(t)
0
( )
0 0
t
tt
δ
∞ =
=
≠
t
( )
t
δ
0
0
0
( ) ( ) ( ) 1
st
F s t e dt t e dt
δ δ
−
+∞ +∞
−
= = =
∫ ∫
{
}
( ) 1
t
δ
=