
XÁC SUẤT THỐNG KÊ KINH TẾ
Đoàn Hồng Chương1
1Bộ môn Toán - TKKT, Đại học Kinh Tế - Luật
Chương 1
NHẮC LẠI VỀ ĐẠI SỐ TỔ HỢP
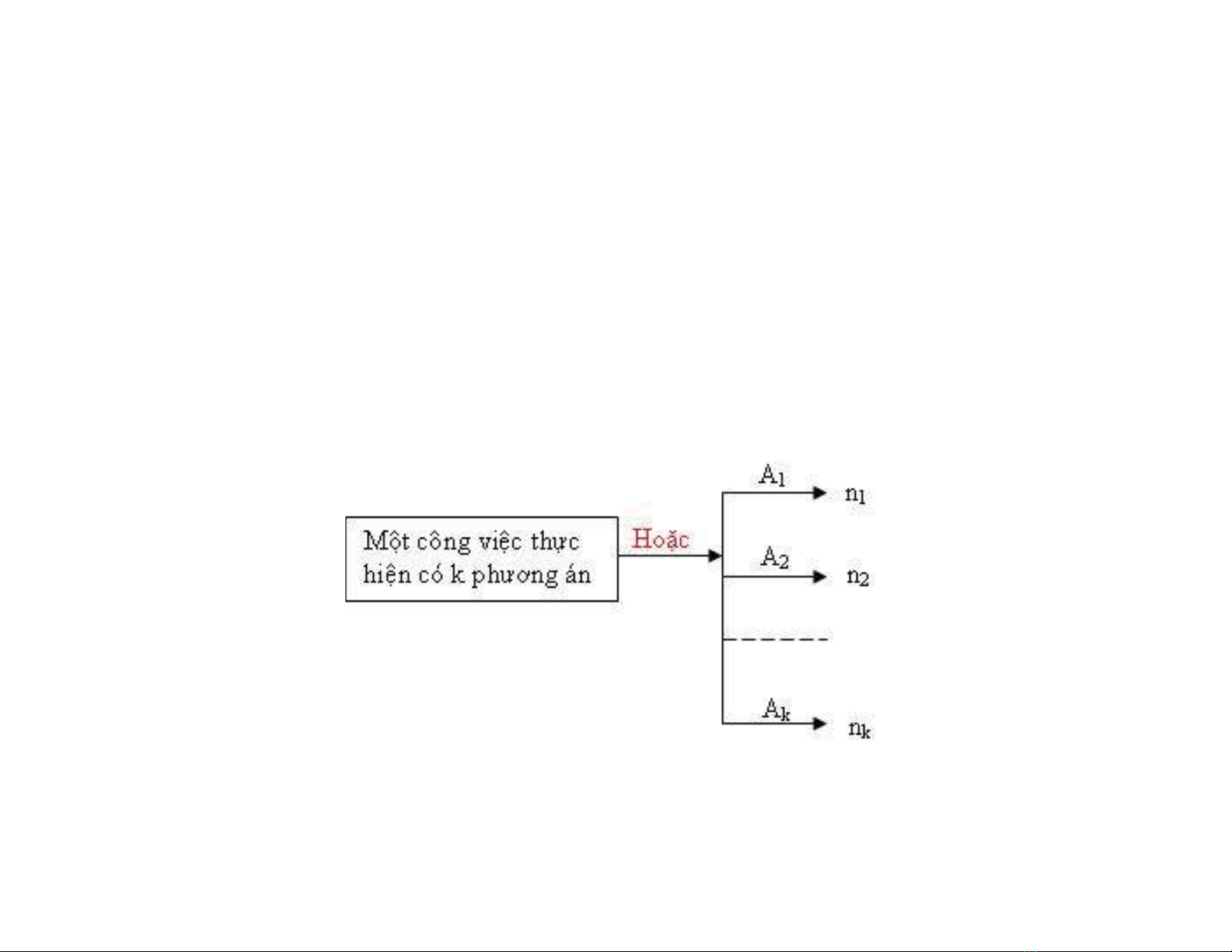
1.1 Qui tắc cộng
Nếu một công việc có thể thực hiện theo k phương án A1,A
2...,A
kvà mỗi
phương án có ni(i=1,2,...,k)cách thực hiện thì số cách thực hiện công
việc là
n=n1+n2+...+nk.(1.1)
Ví dụ 1.1. Một người muốn mua một đôi giày cỡ 39 hoặc 40.Cỡ39 có hai màu đen
và trắng, cỡ 40 có ba màu đen, trắng và nâu. Hỏi người đó có bao nhiêu cách chọn
mua giày? (Đáp số: n=2+3=5).
Trang 1

1.2 Qui tắc nhân
Nếu một công việc bao gồm kgiai đoạn và mỗi giai đoạn có ni(i=1,2, ..., k)
cách thực hiện thì số cách thực hiện công việc là
n=n1.n2...n
k(1.2)
Ví dụ 1.2. Trong một trò chơi, mỗi thí sinh phải trả lời 5câu hỏi trắc nghiệm có sẵn
của ban tổ chức, mỗi câu hỏi có 4lựa chọn. Hỏi mỗi thí sinh có bao nhiêu phương
án trả lời? (Đáp số: n=4
5= 1024).
1.3 Hoán vị
Định nghĩa 1.1. Cho tập hợp gồm nphần tử khác nhau. Mỗi cách sắp xếp nphần
tử theo một thứ tự gọi là một hoán vị.
Trang 2

Tính chất 1.1. Số hoán vị của n phần tử là
Pn=n!(1.3)
•Qui ước: 0! = 1.
Ví dụ 1.3. Một bàn có 4học sinh. Hỏi có bao nhiêu cách xếp chỗ ngồi?
Giải. Vì mỗi cách xếp học sinh vào một bàn dài là một hoán vị nên số cách
xếp là P4=4!=24.
Ví dụ 1.4. Có bao nhiêu cách xếp chỗ ngồi cho 5 bạn học sinh vào một bàn dài biết
rằng 2 bạn Hoa và Lan muốn ngồi cạnh nhau? Hoa và Lan không ngồi cạnh nhau?
Giải. Nếu 2 bạn Hoa và Lan ngồi cạnh nhau thì ta có thể giải bài toán theo
2 bước sau đây:
•Bước 1: Xem 2 bạn Hoa và Lan như là 1 người. Khi đó số cách xếp là số
hoán vị của 4 phần tử
P4=4!=24.
Trang 3

•Bước 2: Đổi chỗ 2 bạn Hoa và Lan. Khi đó số cách xếp là số hoán vị của
2 phần tử
P2=2!=2.
Vậy số cách xếp là n=P4.P2=48.
Trường hợp 2 bạn Hoa và Lan không ngồi cạnh nhau là phần bù của trường
hợp trên. Do đó số cách xếp là hiệu của số cách xếp tùy ý 5 người và số cách
xếp 2 bạn Hoa và Lan ngồi cạnh nhau
n=P5−48 = 5! −48 = 72.
1.4 Chỉnh hợp
Định nghĩa 1.2. Cho tập hợp gồm nphần tử khác nhau. Mỗi cách xếp kphần tử
(1 ≤k≤n)lấy từ nphần tử của tập hợp theo một thứ tự gọi là một chỉnh hợp
chập kcủa n.
Tính chất 1.2. Số chỉnh hợp chập kcủa nphần tử là
Ak
n=n!
(n−k)!.(1.4)
Trang 4


























