5.5 Bài toán so sánh hai tỷ lệ
Bài toán: Giả sử p1,p2tương ứng là tỷ lệ các phần tử
mang dấu hiệu A nào đó của tổng thể thứ nhất và
tổng thể thứ hai.
Mẫu của tổng thể thứ nhất: Thực hiện n1phép thử
độc lập cùng điều kiện, có m1phép thử xảy ra sự kiện
A.
Mẫu của tổng thể thứ hai: Thực hiện n2phép thử độc
lập cùng điều kiện, có m2phép thử xảy ra sự kiện A.
Câu hỏi: Hãy so sánh p1với p2.
107 of 112
Cách giải quyết:
+) Bài toán đặt ra là ta cần so sánh p1và p2.
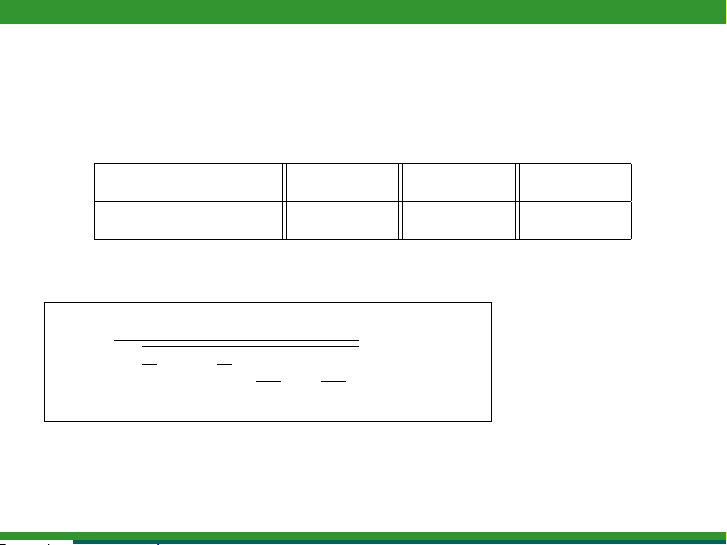
Giả thuyết H0p1=p2p1=p2p1=p2
Đối thuyết H1p16=p2p1>p2p1<p2
108 of 112
Cách giải quyết:
+) Bài toán đặt ra là ta cần so sánh p1và p2.
Giả thuyết H0p1=p2p1=p2p1=p2
Đối thuyết H1p16=p2p1>p2p1<p2
+) Chọn tiêu chuẩn kiểm định:
T=f1−f2
rf(1−f)( 1
n1
+1
n2
)
∼N(0;1)nếu giả thuyết
H0đúng.
108 of 112
+) Từ mẫu thu thập, ta tính được giá trị quan sát:
tqs =f1−f2
rf(1−f)( 1
n1
+1
n2
)
với f1=m1
n1
,f2=m2
n2
,f=m1+m2
n1+n2
=n1.f1+n2.f2
n1+n2
109 of 112
+) Từ mẫu thu thập, ta tính được giá trị quan sát:
tqs =f1−f2
rf(1−f)( 1
n1
+1
n2
)
với f1=m1
n1
,f2=m2
n2
,f=m1+m2
n1+n2
=n1.f1+n2.f2
n1+n2
+) Miền bác bỏ H0được xác định cho 3 trường hợp
như sau:
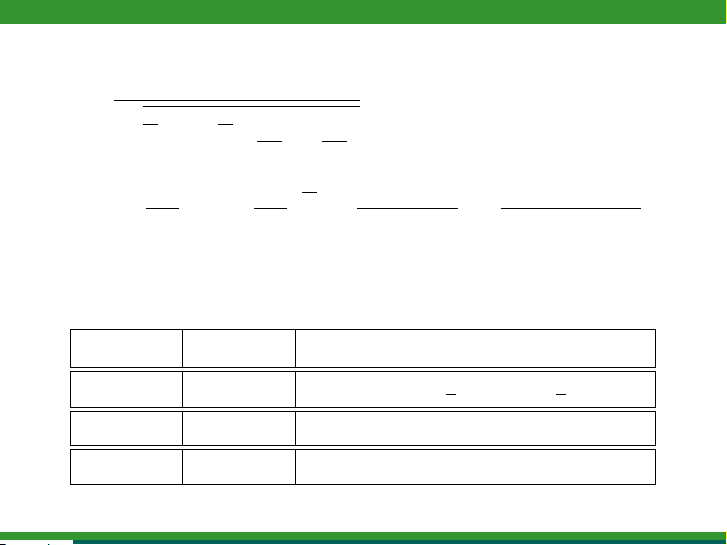
H0H1Miền bác bỏ H0:Wα
p1=p2p16=p2(−∞;−u1−α
2)∪(u1−α
2; +∞)
p1=p2p1>p2(u1−α; +∞)
p1=p2p1<p2(−∞;−u1−α)
109 of 112