Chuyên đề bồi dưỡng học sinh giỏi Thẳng hàng và đồng quy
Vũ Đức Kiên – Trường Thực hành sư phạm, CĐSP Quảng Ninh trang 1
BÀI TOÁ THẲG HÀG
T S PHƯƠNG PHÁP CHNG MINH BA ĐIM THNG HÀNG.
1. Ba điểm A, B, C thẳng hàng theo thứ tự đó khi và chỉ khi
0
ABC = 180
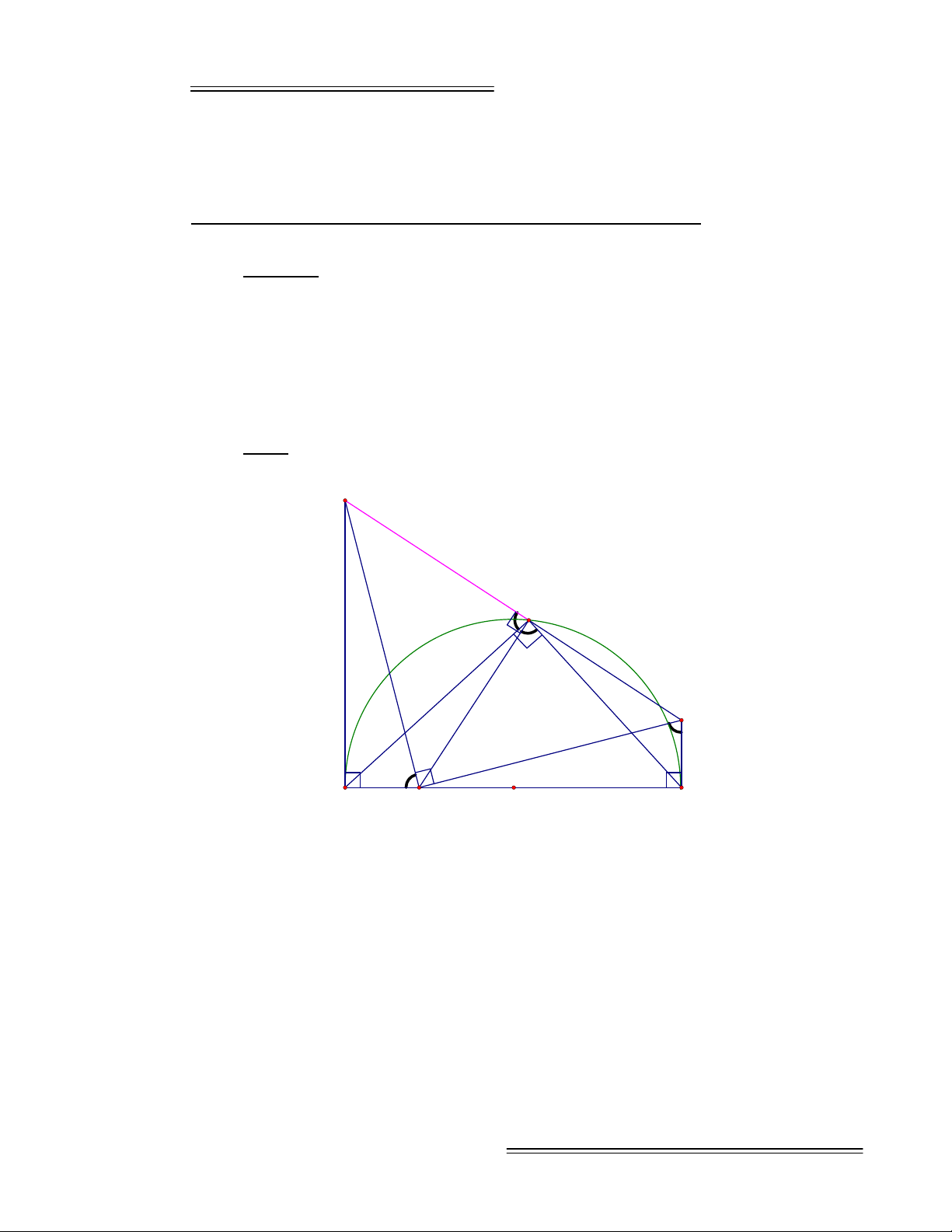
Ví dụ 1: Cho nửa đường tròn đường kính AB. Lấy điểm C thuộc AB
sao cho CA < CB và điểm M thuộc nửa đường tròn đó. Đường thẳng qua M,
vuông góc với MC cắt tiếp tuyến qua A của nửa đường tròn tại N. Đường
thẳng qua C, vuông góc với NC cắt tiếp tuyến qua B của nửa đường tròn tại P.
Chứng minh M, N, P thẳng hàng.
Giải:
M
∈
nửa đường tròn đường kính AB
0
AMB 90
⇒ =
mà
0
NMC 90
=
NMA CMB
⇒ =
Tứ giác ANMC có
0
NAC NMC 180
+ = ⇒
tứ giác ANMC nội tiếp
NMA NCA
⇒ =
lại có
ANC
và
BCP
đồng dạng
NCA CPB
⇒ =
.
Vậy
CMB CPB
=
⇒
tứ giác CMPB nội tiếp
0
CMP 90
⇒ =
0
NMC PMC 180
⇒ + = ⇒
N, M, P thẳng hàng .
Chuyên đề bồi dưỡng học sinh giỏi Thẳng hàng và đồng quy
Vũ Đức Kiên – Trường Thực hành sư phạm, CĐSP Quảng Ninh trang 2
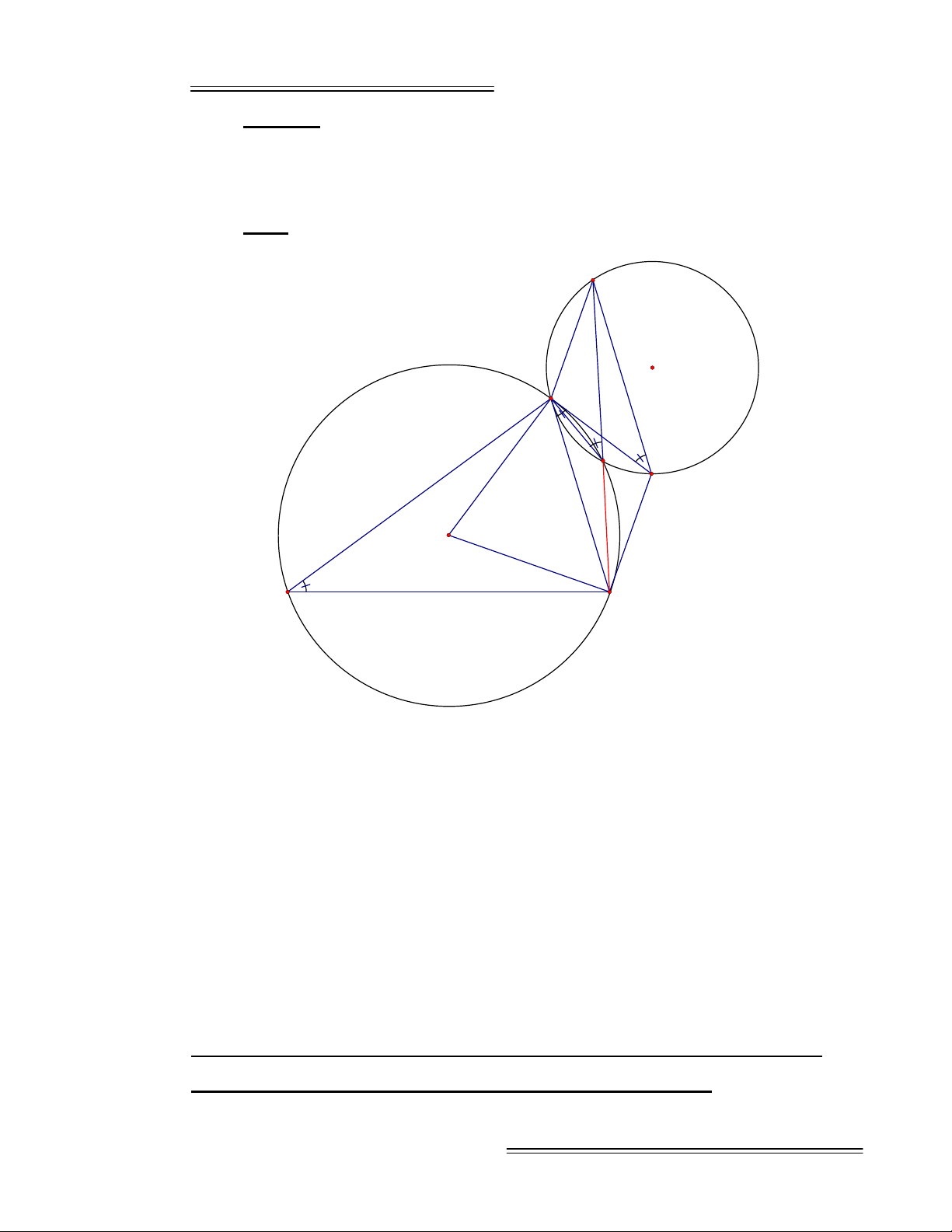
Ví dụ 2:
Cho tam giác ABC nội tiếp đường tròn (O). Các tiếp tuyến qua
A, C cắt nhau ở M. Vẽ hình bình hành ACMN. Đường tròn ngoại tiếp tam
giác AMN cắt (O) ở D. Chứng minh N, D, C thẳng hàng.
Giải:
ADN AMN
=
( hai góc nội tiếp đường tròn ngoại tiếp tam giác AMN cùng
chắn
AN
).
NMA CAM
=
( vì NM // AC )
CAM CBA
=
( góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây của đường
tròn (O) cùng chắn
AC
)
0
CBA CDA 180
+ =
( vì tứ giác ABCD nội tiếp đường tron (O))
Vậy
0
ADN CDA 180
+ =
hay ba điểm N, D, C thẳng hàng.
2. Ba điểm A, B, C thẳng hàng khi và chỉ khi đường thẳng AB và AC cùng
song song hoặc cùng vuông góc với một đường thẳng nào đó.
Chuyên đề bồi dưỡng học sinh giỏi Thẳng hàng và đồng quy
Vũ Đức Kiên – Trường Thực hành sư phạm, CĐSP Quảng Ninh trang 3
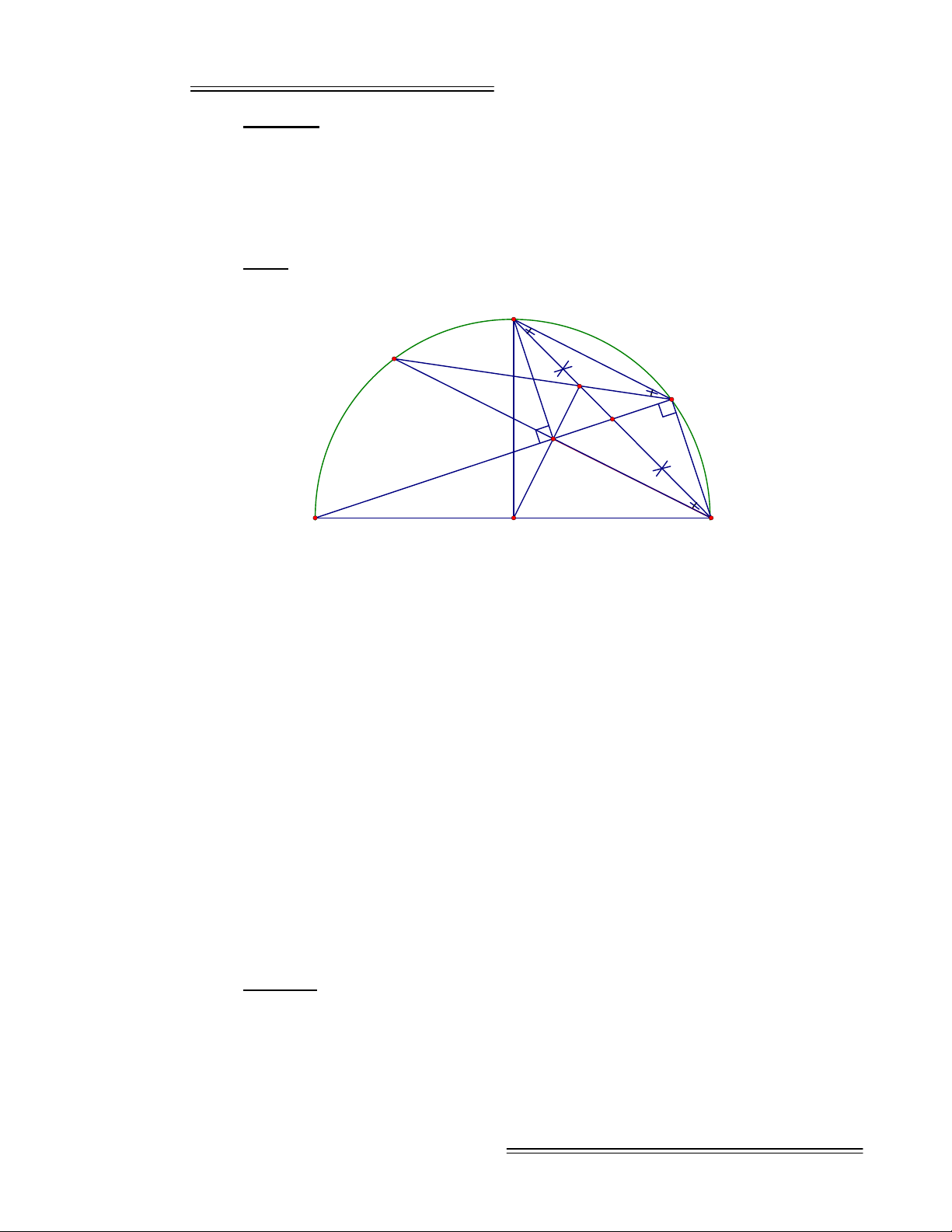
Ví dụ 3:
Cho nửa đường tròn tâm O đường kính AB. Gọi C là trung
điểm của cung AB, K là trung điểm của đoạn BC. AK cắt (O) tại M. Kẻ CH
vuông góc với AM. OH cắt BC tại N. MN cắt (O) tại D. Chứng minh rằng B,
H, D thẳng hàng.
Giải:
0
AMB 90
=
( góc nội tiếp chắn nửa đường tròn đường kính AB) hay
BM AM
⊥
mà
CM AM
⊥
⇒
MB // CH lại có KC = KB nên tam giác KMB =
tam giác KHC
⇒
BH // CM. (1)
lại có OC = OM
⇒
O
∈
trung trực của CM .
0
CMA 45
=
,
0
CHM 90
=
⇒
tam giác CHM vuông cân
CH MH
⇒ =
⇒
H
∈
trung trực của CM. Vậy OH là trung trực của CM.
N
⇒ ∈
trung trực của CM
hay NC = NM
⇒
tam giác NCM cân
NCM NMC
⇒ =
lại có
DMC DBC
=
( hai góc nội tiếp đường tròn (O) cùng chắn
DC
Vậy
BCM CBD
=
⇒
DB // CM (2)
Từ (1) và (2)
⇒
D, H, B thẳng hàng.
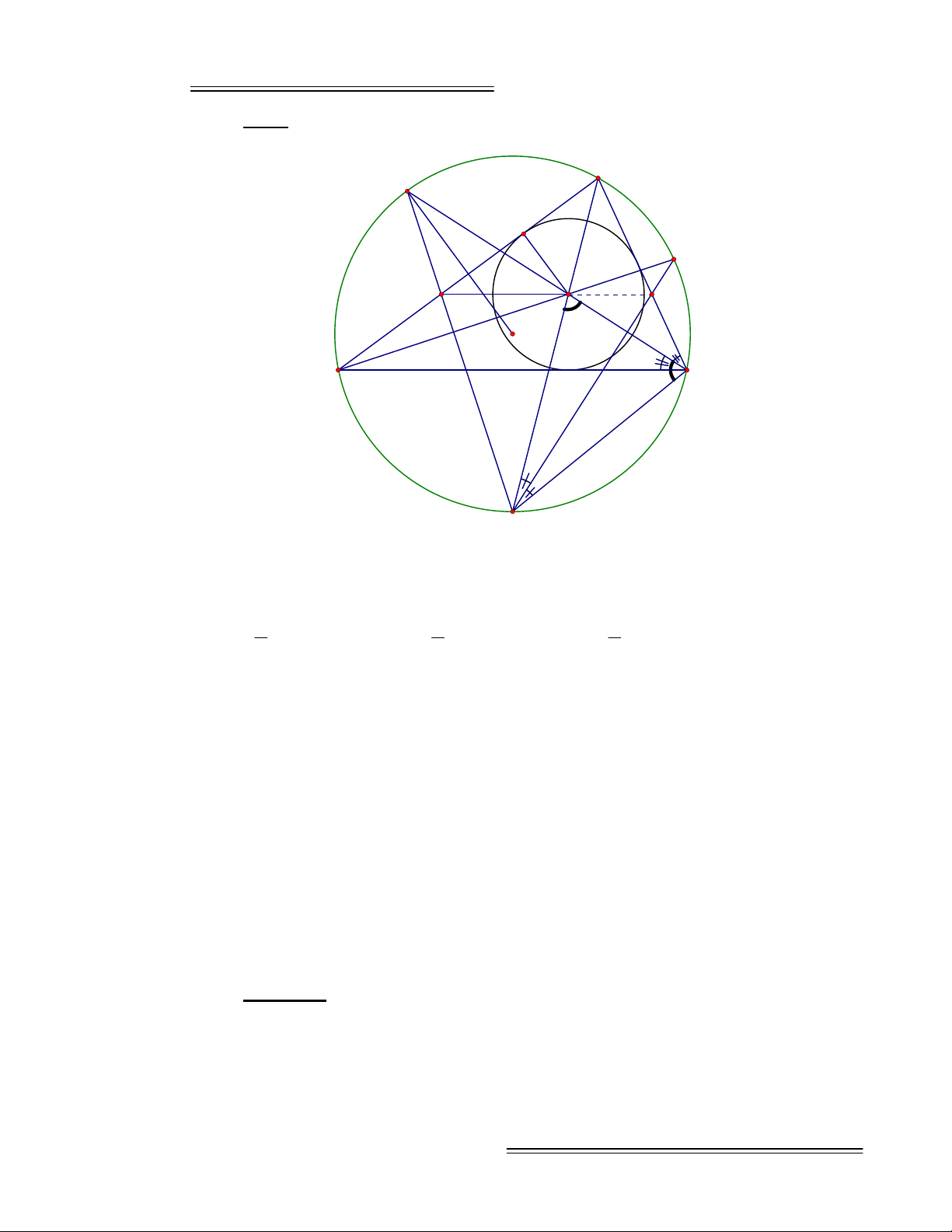
Ví dụ 4:
Cho tam giác ABC nội tiếp đường tròn (O). Gọi
111
A ;B ;C
là
trung điểm của các cung
BC;CA;AB
của đường tròn (O) và I là tâm đường
tròn nội tiếp của tam giác ABC.
1 1
A C
cắt AB ở M,
1 1
A B
cắt AC ở N. Chứng
minh M, I, N thẳng hàng.
Chuyên đề bồi dưỡng học sinh giỏi Thẳng hàng và đồng quy
Vũ Đức Kiên – Trường Thực hành sư phạm, CĐSP Quảng Ninh trang 4
Giải:
Dễ thấy
1 1 1
AA ;BB ;CC
đồng quy tại I.
(
)
(
)
1 1 1 1 1 1 1 1
1 1 1
A IC sdA C sdC A sdA B sdBC sdA C A CI
2 2 2
= + = + = =
⇒
tam
giác
1
A IC
cân.
Lại có
1 1 1 1
AA B CA B
=
(hai góc nội tiếp (O) chắn hai cung bằng nhau
1 1
AB B C
=
Vậy
1 1
A B
là trung trực của IC nên tam giác NIC cân
NIC NIC
⇒ =
mà
NCI ICB
=
NIC ICB
⇒ = ⇒
IN // BC.
Chứng minh tương tự ta được IM // BC.
Vậy N, I, M thẳng hàng.
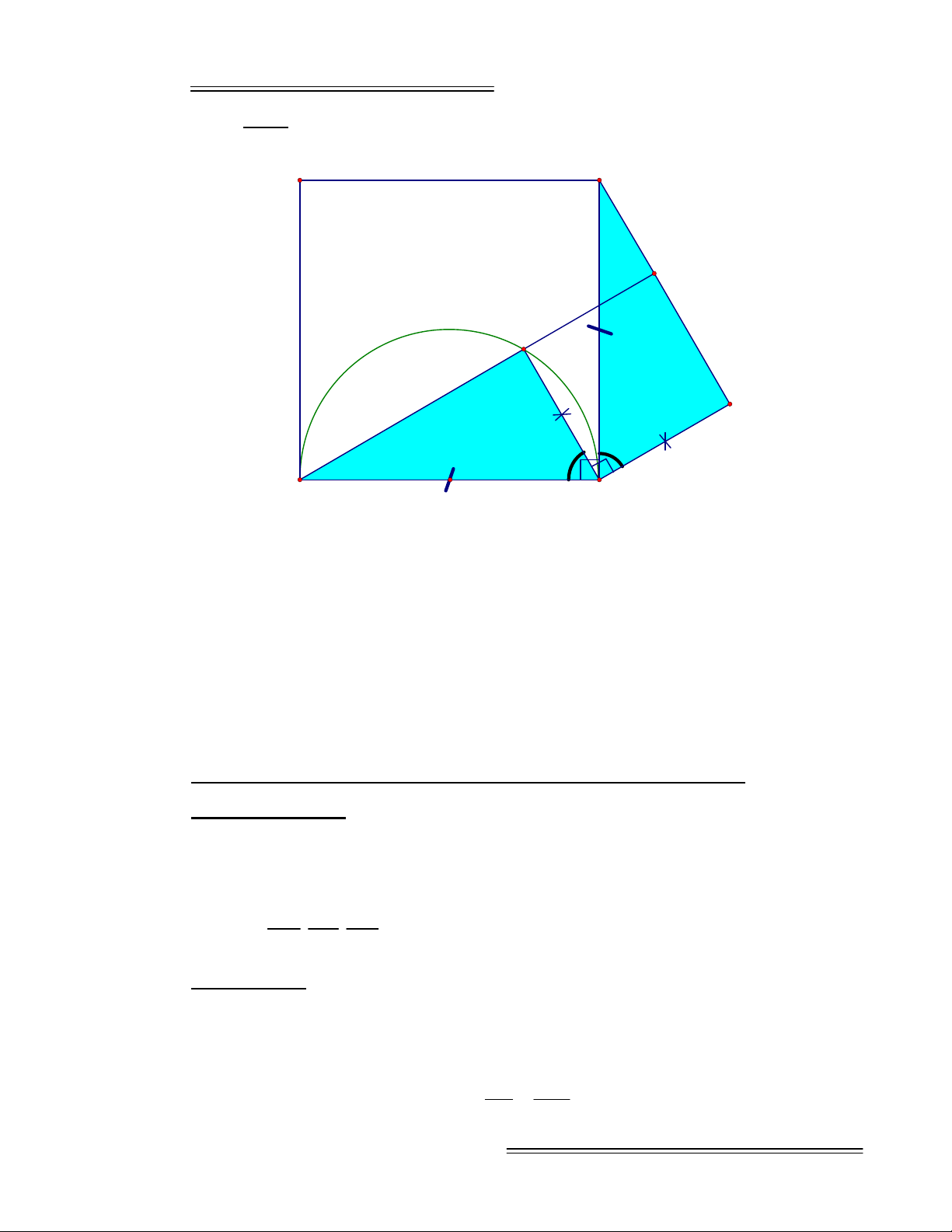
Ví dụ 5:
Cho nửa đường tròn đường kính AB. Về cùng một phía với
nửa đường tròn đó, vẽ hình vuông ABCD. M là điểm tùy ý thuộc nửa đường
tròn. Về phía ngoài tam giác MAB vẽ hình vuông BMNE. Chứng minh C, E,
N thẳng hàng.
Chuyên đề bồi dưỡng học sinh giỏi Thẳng hàng và đồng quy
Vũ Đức Kiên – Trường Thực hành sư phạm, CĐSP Quảng Ninh trang 5
Giải:
Xét tam giác ABM và tam giác CBE có;
Vì
0
ABC MBE 90 ABM CBE
= = ⇒ =
; AB = CB; MB = EB
ABM CBE AMB CEB
⇒ = ⇒ =
Mà
0
AMB 90
=
(góc nội tiếp chắn nửa đường tròn đường kính AB)
Vậy
BE CE
⊥
lại có
BE NE
⊥
vậy E, N, C thẳng hàng.
3. Sử dụng định lí Menelaus vào chứng minh 3 điểm thẳng hàng.
Định lí Menelaus:
Cho tam giác ABC, trên các cạnh AB, AC và phần kéo dài của cạnh CB lần
lượt lấy 3 điểm M, $, P. Khi đó điều kiện cần và đủ để ba điểm M, $, P thẳng
hàng là:
. . 1
=
MA PB $C
MB PC $A
Chứng minh:
*) Giả sử M, 8, P thẳng hàng.
Kẻ CG // PM (
G AB
∈
)
Xét tam giác BMP có GC // MP
PB MB
PC MG
⇒ =


























