
Chương1.Biếncốngẫunhiênvàxácsuất
LêVănPhong‐TrầnTrọngNguyên,ĐHKTQD 1
Ch−¬ng 1
BiÕn cè ngÉu nhiªn vμ x¸c suÊt
Trong thùc tÕ chóng ta th−êng gÆp nh÷ng hiÖn t−îng ngÉu nhiªn, tøc lµ nh÷ng hiÖn
t−îng mµ mÆc dï víi mäi kh¶ n¨ng cã thÓ cã ta cè g¾ng gi÷ cho nh÷ng ®iÒu kiÖn c¬ b¶n
cña c¸c lÇn thÝ nghiÖm vÒ c¸c hiÖn t−îng Êy kh«ng thay ®æi, nh−ng ta vÉn kh«ng thÓ
kh¼ng ®Þnh ®−îc kÕt qu¶ cña tõng thÝ nghiÖm riªng lÎ sÏ nh− thÕ nµo. Së dÜ nh− vËy v×
ngoµi nhãm nh÷ng ®iÒu kiÖn c¬ b¶n ra cßn cã rÊt nhiÒu c¸c nguyªn nh©n kh«ng l−êng
tr−íc ®−îc, g©y t¸c ®éng kh¸c nhau trong qu¸ tr×nh tiÕn hµnh c¸c lÇn thÝ nghiÖm, lµm cho
kÕt qu¶ cña c¸c lÇn thÝ nghiÖm cã thÓ thay ®æi tõ lÇn nµy sang lÇn kh¸c, khiÕn cho mäi cè
g¾ng cña chóng ta ®Ó dù ®o¸n kÕt qu¶ chÝnh x¸c ë mçi lÇn thÝ nghiÖm riªng lÎ ®Òu v«
hiÖu.
Tuy nhiªn, trªn c¬ së quan s¸t rÊt nhiÒu hiÖn t−îng thùc tÕ ng−êi ta thÊy r»ng nÕu nh−
ë mçi thÝ nghiÖm riªng lÎ sù xuÊt hiÖn cña mét sù kiÖn nµo ®ã cßn mang tÝnh chÊt ngÉu
nhiªn th× qua mét sè lín lÇn lÆp l¹i cïng thÝ nghiÖm Êy, kh¶ n¨ng xuÊt hiÖn kh¸ch quan
cña sù kiÖn ®ã l¹i biÓu hiÖn kh¸ râ nÐt. V× vËy mét lý thuyÕt to¸n häc ®· ®−îc x©y dùng
nªn nh»m nghiªn cøu mét c¸ch chÝnh x¸c tÝnh quy luËt cña c¸c hiÖn t−îng ngÉu nhiªn khi
ta lÆp l¹i nhiÒu lÇn cïng c¸c ®iÒu kiÖn c¬ b¶n lµm n¶y sinh ra c¸c hiÖn t−îng ®ã, ®−îc gäi
lµ Lý thuyÕt x¸c suÊt.
A- C¸c ®Þnh nghÜa vÒ x¸c suÊt
I. PhÐp thö vμ kh«ng gian c¸c biÕn cè s¬ cÊp
Trong lý thuyÕt x¸c suÊt, khi thùc hiÖn mét nhãm c¸c ®iÒu kiÖn c¬ b¶n nµo ®ã ng−êi
ta gäi lµ thùc hiÖn mét phÐp thö. NÕu kÕt qu¶ cña phÐp thö mµ kh«ng thÓ kh¼ng ®Þnh tr−íc
®−îc th× ta cã mét phÐp thö ngÉu nhiªn. Ta sÏ ký hiÖu phÐp thö ngÉu nhiªn lµ G.
C¸c kÕt qu¶ cã thÓ x¶y ra trong phÐp thö G sao cho khi G ®−îc thùc hiÖn th× thÓ nµo
còng cã mét trong chóng x¶y ra, chóng lo¹i trõ lÉn nhau vµ kh«ng thÓ ph©n chia thµnh

Chương1.Biếncốngẫunhiênvàxácsuất
LêVănPhong‐TrầnTrọngNguyên,ĐHKTQD 2
nh÷ng kÕt qu¶ nhá h¬n th× c¸c kÕt qu¶ nh− vËy ®−îc gäi lµ c¸c biÕn cè s¬ cÊp. Nãi c¸ch
kh¸c mét biÕn cè s¬ cÊp lµ mét kÕt qu¶ tèi gi¶n cña phÐp thö.
TËp hîp tÊt c¶ c¸c biÕn cè s¬ cÊp ω cña phÐp thö G ®−îc gäi lµ kh«ng gian c¸c biÕn
cè s¬ cÊp (kh«ng gian mÉu) víi ký hiÖu lµ Ω.
ThÝ dô 1. NÕu phÐp thö lµ “tung mét ®ång xu” th× Ω= { S, N } trong ®ã: ω1= S = kÕt
qu¶ lµ sÊp; ω2 = N = kÕt qu¶ lµ ngöa.
ThÝ dô 2. NÕu phÐp thö lµ “tung mét h¹t xóc s¾c” th×: Ω={1,2,3,4,5,6}
trong ®ã : ωi= i = ®−îc mÆt i chÊm (i= 6,1)
ThÝ dô 3. NÕu phÐp thö lµ “tung cïng mét lóc hai ®ång xu” th× :
Ω={(S,S), (S,N), (N,S), (N,N)}
ThÝ dô 4. NÕu phÐp thö lµ “Tung cïng mét lóc hai h¹t xóc s¾c” th×:
Ω ={(x,y): x= 6,1 ;y= 6,1 }
ThÝ dô 5. NÕu phÐp thö lµ "tung mét ®ång xu cho tíi khi nµo ®−îc mÆt sÊp th× dõng" th×:
,...}NNNS,NNS,NS,S{=Ω
ThÝ dô 6. NÕu phÐp thö lµ "®o kho¶ng c¸ch tõ ®iÓm ch¹m cña viªn ®¹n tíi t©m bia víi
b¸n kÝnh cña bia lµ mét ®¬n vÞ ®é dµi th× =Ω[0,1[.
NhËn xÐt :
a. Sè l−îng c¸c phÇn tö cña Ω trong c¸c thÝ dô 1, 2, 3, 4 lµ h÷u h¹n.
b. Sè l−îng c¸c phÇn tö cña Ω trong thÝ dô 5 lµ v« h¹n nh−ng ®Õm ®−îc (tøc lµ ta cã thÓ
®¸nh sè ®−îc 1
ω= S, 2
ω= NS, 3
ω= NNS,....).
C¸c tËp h÷u h¹n hay v« h¹n ®Õm ®−îc gäi lµ c¸c tËp h¬p rêi r¹c.
c. Sè l−îng c¸c phÇn tö cña Ω trong thÝ dô 6 (sè c¸c ®iÓm cña ®o¹n [0,1[) lµ v« h¹n
nh−ng ®Õm ®−îc. Trong tr−êng hîp nµy ta b¶o Ω cã lùc l−îng continum.
II. - ®¹i sè c¸c biÕn cè
1. BiÕn cè ngÉu nhiªn
Mét biÕn cè ngÉu nhiªn A lµ mét tËp hîp con cña Ω
Chương1.Biếncốngẫunhiênvàxácsuất
LêVănPhong‐TrầnTrọngNguyên,ĐHKTQD 3
ThÝ dô 1: Gäi A lµ biÕn cè “®−îc mÆt cã sè chÊm lµ béi cña 3” khi tung h¹t xóc s¾c th×
A={3,6}⊂ Ω.
Ghi chó
a. KÕt qu¶ ωnµo cña G mµ lµm cho A x¶y ra th× kÕt qu¶ ®ã ®−îc gäi lµ kÕt qu¶ thuËn lîi
cho A. Nh− vËy biÕn cè A ë thÝ dô võa nªu cã hai kÕt qu¶ thuËn lîi.
b. Mçi biÕn cè s¬ cÊp ωcòng cã thÓ coi lµ mét biÕn cè ngÉu nhiªn {ω} (gåm mét phÇn
tö ).
c. Ω ®−îc gäi lµ biÕn cè ch¾c ch¾n.
d. TËp hîp trèng φ ®−îc gäi lµ biÕn cè kh«ng thÓ cã.
C¸c kh¸i niÖm võa nªu cã thÓ minh häa trong h×nh sau
2. Mèi quan hÖ gi÷a c¸c biÕn cè
Stone ®· chøng minh ®−îc r»ng: gi÷a c¸c tËp hîp vµ c¸c biÕn cè cã mét sù ®¼ng cÊu.
V× vËy ta cã thÓ dïng mèi quan hÖ gi÷a c¸c tËp hîp ®Ó m« t¶ mèi quan hÖ gi÷a c¸c biÕn
cè. Cô thÓ:
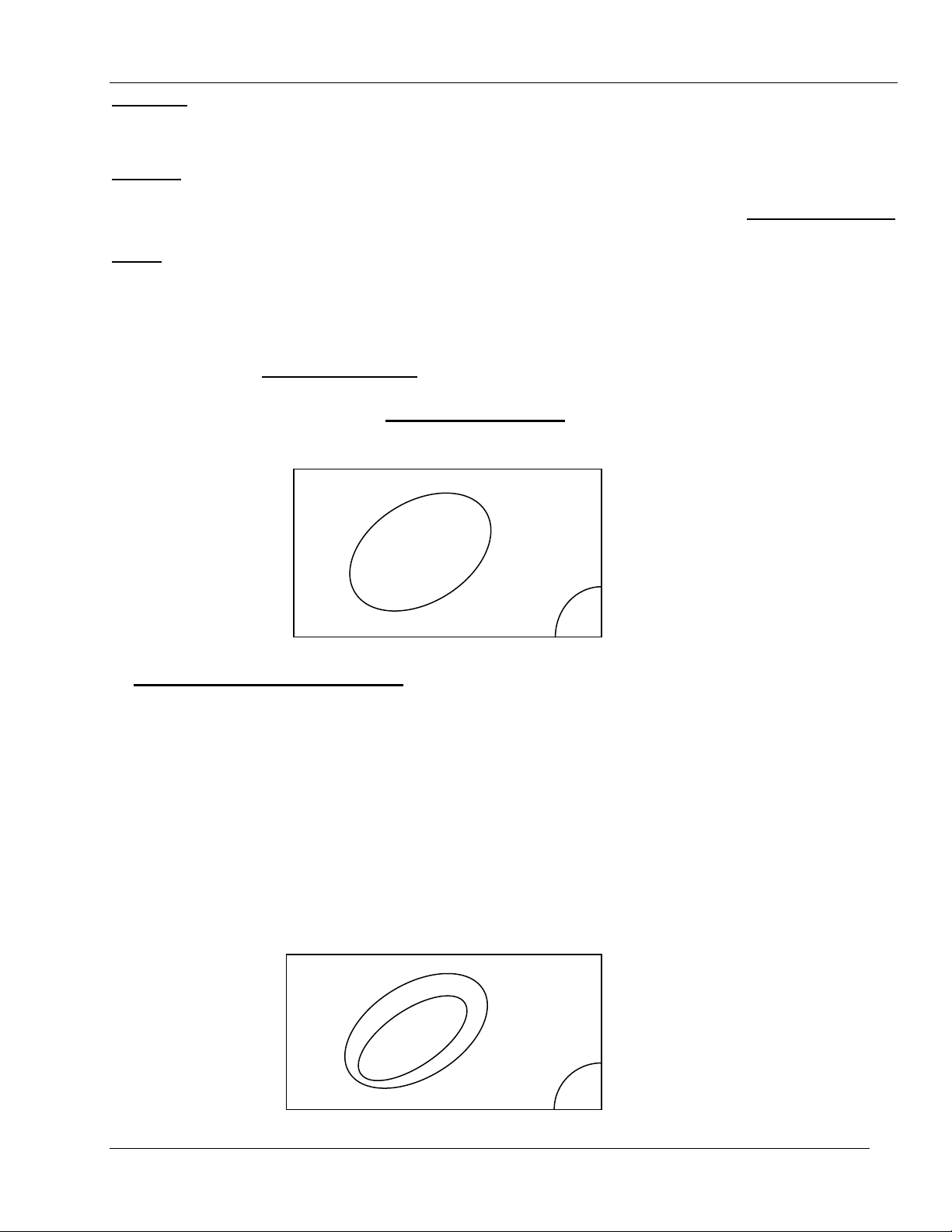
a. NÕu B ⊂ A th× biÕn cè B gäi lµ kÐo theo biÕn cè A. Nh− vËy c¸c phÇn tö ω cña Ω
thuéc B còng sÏ thuéc A (H×nh 1.1). Nãi c¸ch kh¸c biÕn cè B x¶y ra còng lµm cho biÕn cè
A x¶y ra.
H×nh 1.1
A
Ω
x x
x x x
ω
A
Ω
B x x
xx
Chương1.Biếncốngẫunhiênvàxácsuất
LêVănPhong‐TrầnTrọngNguyên,ĐHKTQD 4
ThÝ dô 2:
Gäi B lµ biÕn cè “®−îc mÆt 3 chÊm” tøc lµ B = {3}.
Khi ®ã B ⊂ A = {3, 6} = biÕn cè “®−îc mÆt cã sè chÊm lµ béi cña 3”.
b. NÕu B ⊂ A vµ A ⊂ B th× A vµ B gäi lµ hai biÕn cè t−¬ng ®−¬ng vµ ®−îc ký hiÖu lµ
A=B.
ThÝ dô 3: Gi¶ sö mçi chÊm ®−îc 5 ®iÓm nÕu A lµ biÕn cè “®−îc mÆt 6 chÊm” vµ B lµ biÕn
cè “ng−êi tung ®−îc 30 ®iÓm” th× A = B.
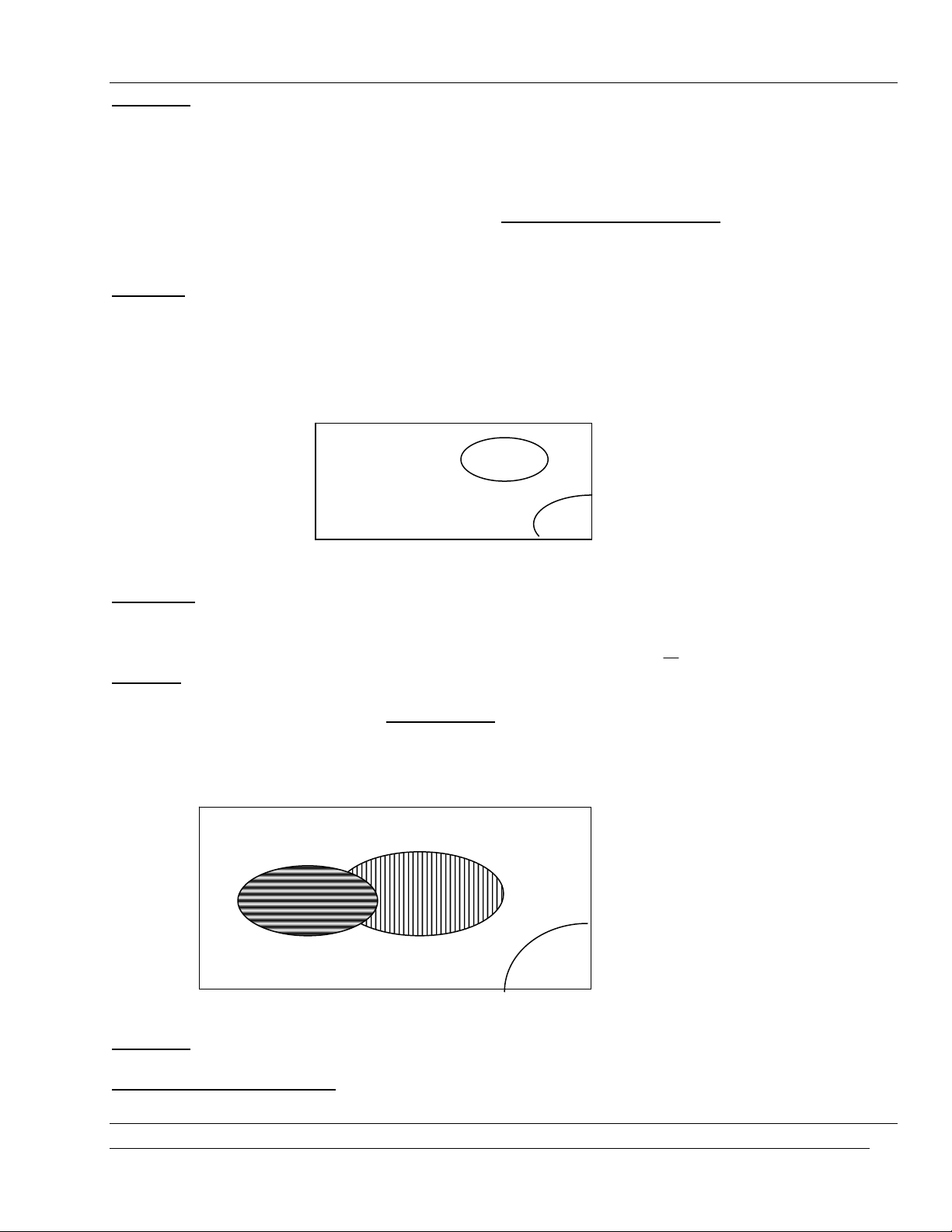
c. NÕu B = Ω\ A th× B gäi lµ biÕn cè ®èi lËp cña A. Nh− vËy B sÏ x¶y ra khi A kh«ng x¶y
ra (H×nh 1.2)*
H×nh 1.2
ThÝ dô 4: NÕu A ={3, 6}= biÕn cè “®−îc mÆt cã sè chÊm lµ béi cña 3” th× B = Ω\{3,
6}={1, 2, 4, 5} lµ biÕn cè “®−îc mÆt cã sè chÊm kh«ng chia hÕt cho 3”.
Ghi chó: BiÕn cè ®èi lËp cña biÕn cè A th−êng ®−îc ký hiÖu lµ A.
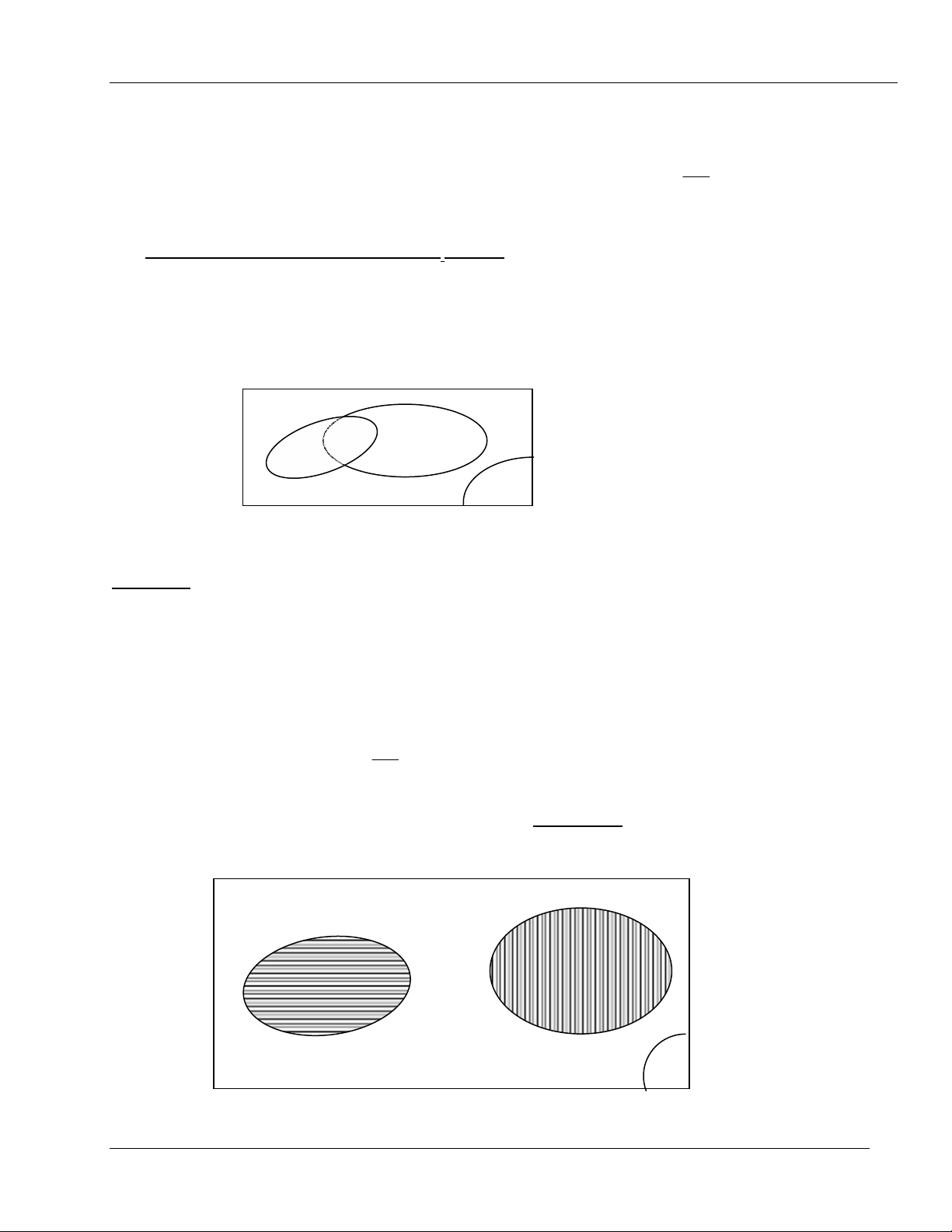
d. NÕu C = A ∪ B th× C gäi lµ biÕn cè tæng cña hai biÕn cè A vµ B. Nh− vËy C sÏ x¶y ra
khi Ýt nhÊt cã mét trong hai biÕn cè A hoÆc B x¶y ra (H×nh 1.3)
ta còng cã thÓ ký hiÖu C = A + B
H×nh 1.3
ThÝ dô 5: NÕu A={3, 6}= BiÕn cè “®−îc mÆt cã sè chÊm lµ béi cña 3”
* (*)TÊt c¶ c¸c thÝ dô trong môc nµy sÏ ®−îc xÐt trong phÐp thö “ tung mét h¹t sóc s¾c” khi ®ã Ω={1,2,3,4,5,6}
A B
Ω
B
Ω
A
Chương1.Biếncốngẫunhiênvàxácsuất
LêVănPhong‐TrầnTrọngNguyên,ĐHKTQD 5
B ={2,4,6} = BiÕn cè “®−îc mÆt cã sè chÊm lµ ch½n ”
th× C = A ∪ B ={2,3,4,6}= BiÕn cè “ ®−îc mÆt ch½n hoÆc béi 3 ”.
T−¬ng tù biÕn cè tæng ∪
n
1=i
i
A cña n biÕn cè thµnh phÇn Ai (i= n,1 ) lµ biÕn cè sÏ x¶y ra
khi Ýt nhÊt cã mét trong c¸c biÕn cè Ai x¶y ra.
e. NÕu C = A ∩ B th× C gäi lµ biÕn cè tÝch cña hai biÕn cè A vµ B. Nh− vËy C sÏ x¶y ra
khi A vµ B ®Òu x¶y ra. (H×nh 1.4)
Ta còng cã thÓ ký hiÖu C = A.B
H×nh 1.4
ThÝ dô 6: NÕu A ={3,6} = BiÕn cè “®−îc mÆt cã sè chÊm lµ béi cña 3”
B ={2,4,6} = BiÕn cè “®−îc mÆt cã sè chÊm lµ ch½n”.
th× C = A ∩ B ={6}= BiÕn cè “®−îc mÆt 6 chÊm”( võa lµ ch½n võa lµ béi cña 3)
T−¬ng tù biÕn cè tÝch ∩
n
1=i
i
A cña n biÕn cè thµnh phÇn Ailµ biÕn cè sÏ x¶y ra khi tÊt c¶
c¸c biÕn cè A i ®Òu x¶y ra (i= n,1 )
f. NÕu A ∩ B = φ th× A vµ B gäi lµ hai biÕn cè xung kh¾c. Nh− vËy A vµ B sÏ kh«ng thÓ
cïng x¶y ra trong phÐp thö (H×nh 1.5)
H×nh 1.5
B
A
Ω
B
A
Ω


























