Chương 12
CẢM ỨNG ĐIỆN TỪ
12.1 Các định luật về hiện tượng cảm ứng điện từ
12.1.1 Thí nghiệm Faraday
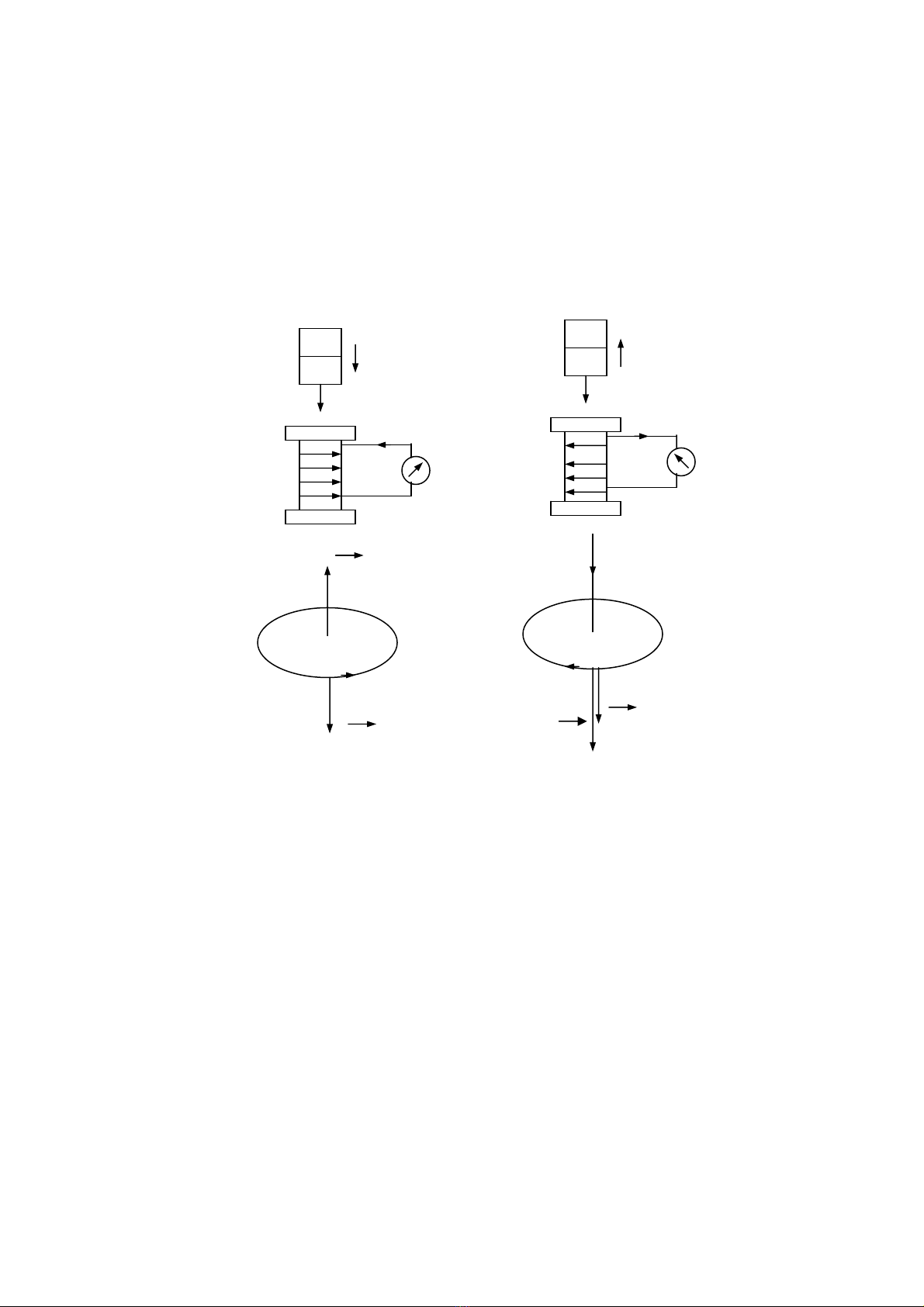
Thí nghiệm gồm nam châm vĩnh cửu, ống dây điện được nối với điện kế G thành một
mạch điện kín. Thí nghiệm được bố trí như hình 12-1.
G
S
N
B’
B
IC
G
B
S
N
B’
IC
a. Khi đưa nam châm vào b. Khi đưa nam châm ra
trong lòng ống dây khỏi ống dây
Hình 12-1
Thí nghiệm chứng tỏ:
- Nếu đưa thanh nam châm vào trong lòng ống dây thì kim điện kế sẽ lệch: trong
ống dây xuất hiện dòng điện. Đó là dòng điện cảm ứng.
- Nếu đưa thanh nam châm ra dòng điện cảm ứng Ic sẽ có chiều ngược lại.
- Di chuyển thanh nam châm càng nhanh thì Ic càng lớn.
Qua thí nghiệm Faraday đã rút ra những kết luận tổng quát sau:
a. Sự biến đổi φm qua mạch kín là nguyên nhân sinh ra dòng điện cảm ứng trong
mạch.
b. Dòng điện cảm ứng chỉ tồn tại trong thời gian φm gửi qua mạch thay đổi.
c. Dòng điện cảm ứng tỉ lệ với tốc độ biến thiên của φm.
d. Chiều của dòng điện cảm ứng phụ thuộc vào φm gửi qua mạch tăng hay giảm.
137
12.1.2 Định luật Lenx
Nghiên cứu hiện tượng cảm ứng điện từ, Lenx đã tìm ra định luật tổng quát về
chiều của dòng điện cảm ứng, gọi là định luật Lenx:
Dòng điện cảm ứng phải có chiều sao cho từ trường do nó sinh ra có tác dụng
chống lại nguyên nhân đã sinh ra nó.
Ta vận dụng định luật này để xác định chiều của dòng điện cảm ứng trong hai
trường hợp ở hình 12-1.
- Trường hợp hình 12-1a, nguyên nhân gây ra dòng điện cảm ứng là do dịch
chuyển cực bắc của thanh nam châm vào trong lòng ống dây, làm cho từ thông gửi qua
ống dây theo chiều từ trên xuống tăng. Theo định luật Lenx, dòng điện cảm ứng Ic phải
có chiều sao cho từ trường do nó sinh ra chống lại sự tăng đó: tức là phải ngược
chiều với từ trường của nam châm. Biết
B'
GB'
G
B
GB'
G
, dùng quy tắc vặn đinh ốc ta có thể xác
định được chiều của dòng điện cảm ứng Ic như trên hình 12-1a.
- Trường hợp hình 12-1b, nguyên nhân gây ra dòng điện cảm ứng là do dịch
chuyển cực bắc của thanh nam châm ra xa ống dây, làm cho từ thông gửi qua ống dây
theo chiều từ trên xuống giảm. Theo định luật Lenx, dòng điện cảm ứng Ic phải có
chiều sao cho từ trường do nó sinh ra chống lại sự giảm đó: tức là phải cùng
chiều với từ trường của nam châm. Biết
B'
GB'
G
B
GB'
G
, dùng quy tắc vặn đinh ốc ta có thể xác
định được chiều của dòng điện cảm ứng Ic như trên hình 12-1b.
12.1.3 Định luật cơ bản của hiện tượng cảm ứng điện từ:
Sự xuất hiện của dòng điện cảm ứng trong mạch chứng tỏ trong mạch có một suất
điện động. Suất điện động ấy gọi là suất điện động cảm ứng.
Dịch chuyển một vòng dây kín (C) trong từ trường, giả sử trong khoảng thời
gian dt từ thông qua (C) biến thiên một lượng dφm: có dòng Ic trong vòng dây (C)
(hình 12-2).
n
G
t+dt
+
c
I
t
n
G
+
Hình 12-2
138
Công của lực từ tác dụng lên Ic là:
dA = I
cdφm
dA là công cản. Để dịch chuyển (C) ta tốn một công dA’ = -dA = -Icdφm. Theo định
luật bảo toàn và chuyển hóa năng lượng: dA’ biến thành năng lượng của dòng điện Ic:
ecIcdt với ec là suất điện động cảm ứng, ta có:
e
cIcdt = -Icdφm
Suy ra: dt
d
em
c
φ
−= (12-1)
Định luật: Suất điện động cảm ứng luôn bằng về trị số nhưng trái dấu với tốc độ biến
thiên của từ thông qua diện tích của mạch điện.
12.1.4 Nguyên tắc tạo ra dòng điện xoay chiều
Dựa vào hiện tượng cảm ứng điện từ, khi cho khung dây quay trong một từ
trường đều thì trong khung dây sẽ xuất hiện suất điện động biến thiên theo quy luật
hàm số sin đối với thời gian: đó chính là nguyên tắc tạo ra dòng điện xoay chiều.
12.2 Hiện tượng tự cảm
12.2.1 Thí nghiệm về hiện tượng tự cảm
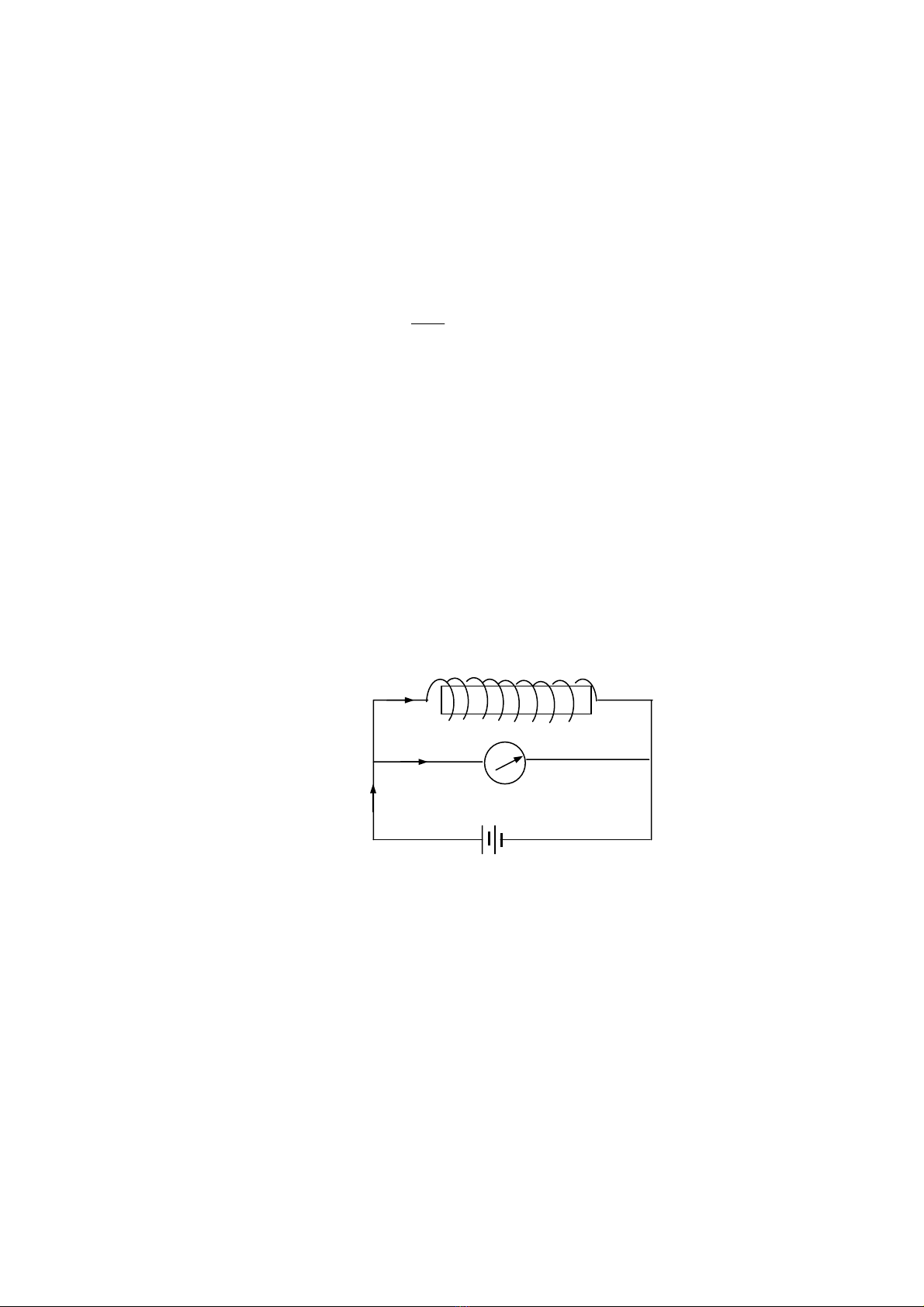
Giả sử mạch điện kín, kim điện kế G nằm ở vị trí a nào đó (hình 12-3).
- Nếu ngắt mạch điện, ta thấy kim điện kế G lệch về quá vị trí số 0 rồi mới quay trở
lại số 0.
- Nếu đóng mạch, kim điện kế lệch quá vị trí a lúc nãy rồi mới quay lại vị trí a.
Giải thích:
- Khi ngắt K: φm qua mạch biến thiên Ic cùng chiều với I qua mạch, Ic phóng qua
điện kế G làm kim của G lệch quá vị trí 0 rồi mới quay về 0.
- Khi đóng K: Ic ngược chiều với I qua ống dây, dòng điện qua nhánh có điện kế G
nhiều hơn do đó kim điện kế G vượt quá vị trí a rồi sau đó mới về vị trí a.
⇒ Hiện tượng trên gọi là hiện tượng tự cảm, dòng điện xuất hiện trong mạch gọi là
dòng tự cảm.
+ -
0a
G
I
Hình 1
2
-
3
139
12.2.2 Suất điện động tự cảm
Theo định luật cơ bản của hiện tượng cảm ứng điện từ:dt
d
ξm
tc
φ
−=
Mặt khác: B
m≈
φ
mà ⇒
IB ≈I
m
≈
φ
⇒ L.I
m
=
φ
L là hệ số tỉ lệ phụ thuộc vào hình dạng, kích thước của mạch điện và tính chất của
môi trường trong đó đặt mạch điện, gọi là hệ số tự cảm. Với một mạch điện nhất định
L là hằng số.
Suy ra: dt
LdI
ξtc −= (12-2)
12.2.3 Hệ số tự cảm
Hệ số tự cảm
I
Lm
φ
−= (12-3)
trong hệ SI: L có đơn vị là Henry (H)
Hệ số tự cảm của ống dây điện thẳng dài vô hạn:
I
l
n
μμInμμB000 ==
2
m0
2
m0
n.S
nBS μμ I
l
n.S
Lμμ
Il
φ
φ
==
⇒= =
(12-4)
12.3 Hiện tượng hỗ cảm
12.3.1 Hiện tượng
Hai mạch điện kín (C1) và (C2) đặt cạnh nhau có I1 và I2 chạy qua. Nếu I1 và I2
đồng thời biến thiên thì từ thông do mỗi mạch sinh ra và gửi qua diện tích của mạch
kia cũng thay đổi ⇒ cả hai mạch đều xuất hiện dòng điện Ic. Hiện tượng đó gọi là hiện
tượng hỗ cảm, các dòng điện Ic gọi là dòng điện hỗ cảm.
12.3.2 Suất điện động hỗ cảm, hệ số hỗ cảm
Theo định luật cơ bản của hiện tượng cảm ứng điện từ ξhệ = d
t
dm
φ
. Gọi:
- m12
φ
: là từ thông do I1 gửi qua mạch điện (C2): 1m12 I
≈
φ
→ 112m12 IM
=
- m21
φ
: là từ thông do I2 gửi qua mạch điện (C1) . 2m21 I
≈
φ
→ 221
1
m2 IM
=
φ
140
12
Mvà là hệ số hỗ cảm của (C
21
M1) và (C2); (C2) và (C1). Người ta đã chứng minh
được rằng: M12 = M21 = M
d
t
dI
M
d
t
L
ξ1m12
hc2 −=−=
φ
(12-5)
d
t
dI
M
d
t
L
ξ2m21
hc1 −=−=
φ
(12-6)
M cũng có thứ nguyên như L (đơn vị là H ).
12.4 Năng lượng từ trường
12.4.1 Năng lượng từ trường của ống dây điện
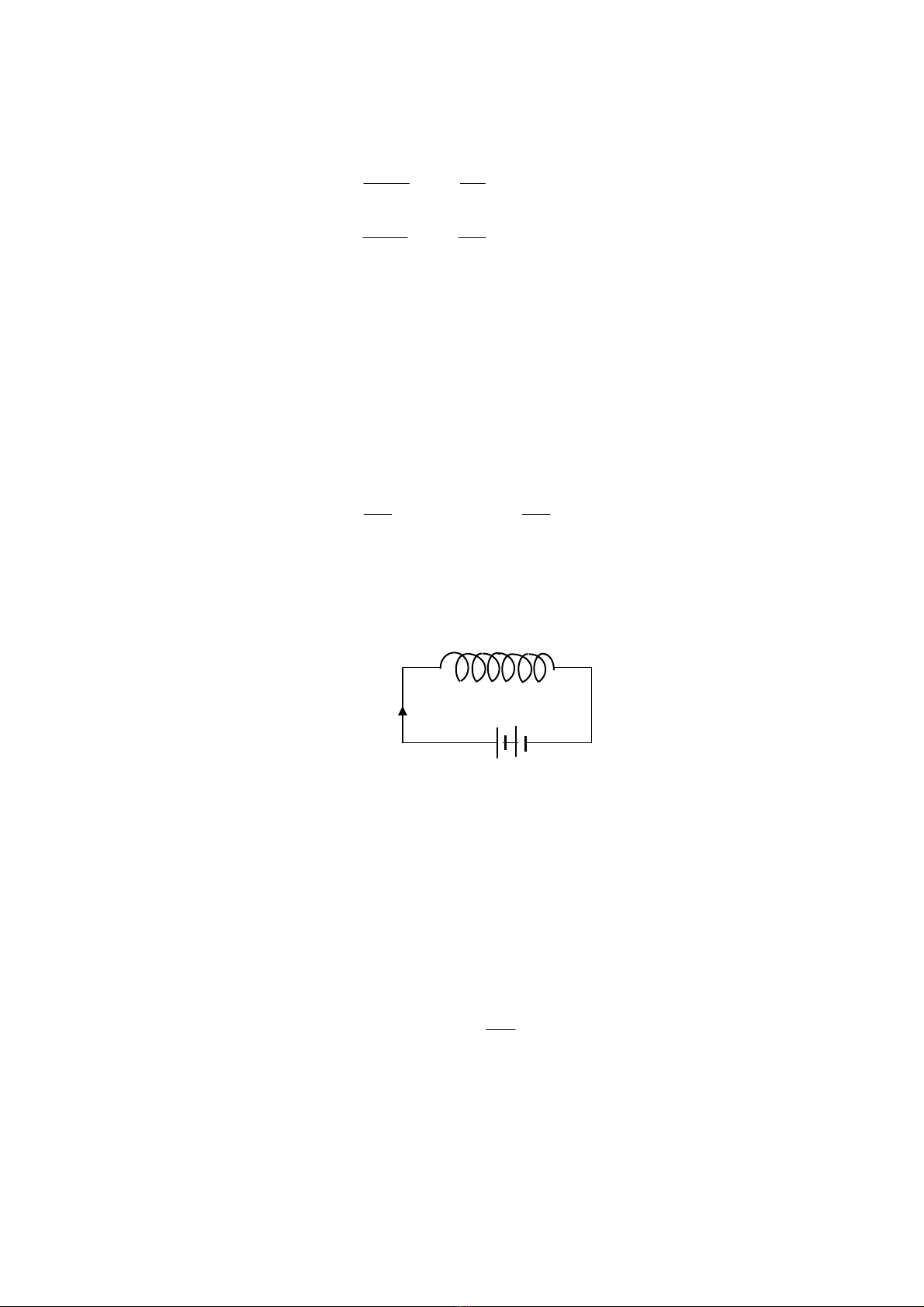
Xét mạch điện gồm một bộ nguồn và một ống dây điện được mắc như hình 12-4.
Lúc mạch điện đóng, áp dụng định luật Ohm cho mạch điện:
ξ+ ξtc = Ri
⇒ dt
Ldi
RiξRi
dt
Ldi
ξ+=⇒=−
Nhân hai vế biểu thức trên cho idt ta được:
LididtRiξidt 2+=
L
I
−
+
Hình 12-4
trong đó:
ξidt : năng lượng do nguồn sinh ra trong khoảng thời gian dt
dtRi2: phần điện năng chuyển sang nhiệt trên R
m
dWLidi =: phần điện năng tiềm tàng trong cuộn dây dưới dạng năng lượng từ trường.
Trong cả quá trình thành lập dòng điện, năng lượng từ trường trong ống dây là:
2
LI
LididWW
2
I
0
W
0
mm
m
=== ∫∫ (12-7)
12.4.2 Năng lượng từ trường
Gọi V = Sl là thể tích của ống dây ⇒ mật độ năng lượng từ trường trong ống
dây được tính:
141