Chương 8:
HỒI QUI VÀ TƯƠNG
QUAN TUYẾN TÍNH
I. Tương quan tuyến tính :
Xét hai biến ngẫu nhiên Yvà Xcó quan hệphụ
thuộc tuyến tính. Giảsửbiến X–biến độc lập,
biến Y–biến phụthuộc vào Xvà từtổng thểMta
lấy mẫu quan sát Xvà Y.
Có hai cách chọn mẫu:
Cách thứnhất: Cố định X, chẳng hạn . Ứng với
ta có một tổng thểcon Micủa M, i = 1, …, n. Từ
Mita lấy ngẫu nhiên các thểvà xác định . Ở đây Y
là biến ngẫu nhiên và mẫu lý thuyết có dạng, còn
mẫu thực nghiệm được viết.
Cách thứhai: Chọn ngẫu nhiên ncá thểtừM và
trên mỗi các thểquan sát Xvà Y. Ở đây Xvà Y
đều là biến ngẫu nhiên và ta có thểdùng hệsố
tương quan giữa Xvà Y để đưa ra các kết luận
thống kê, trong khi đó cách thứnhất không thể
làm như vậy được. Mẫu lý thuyết có dạng
và mẫu thực nghiệm:
.
Không phụthuộc vào cách chọn mẫu, có hai
bước sơ khởi xác định mức độ quan hệtuyến
tính giữa Xvà Y.
11 2 2
( , ), ( , ),..., ( , )
nn
X
YXY XY
11 2 2
( , ), ( , ),..., ( , )
nn
x
yxy xy
Bước thứnhất: Vẽcác điểm trên hệtọa độ xOy.
Dựa vào đồ thị ta đưa ra phỏng đoán vềsựphụ
thuộc tuyến tính giữXvà Y.
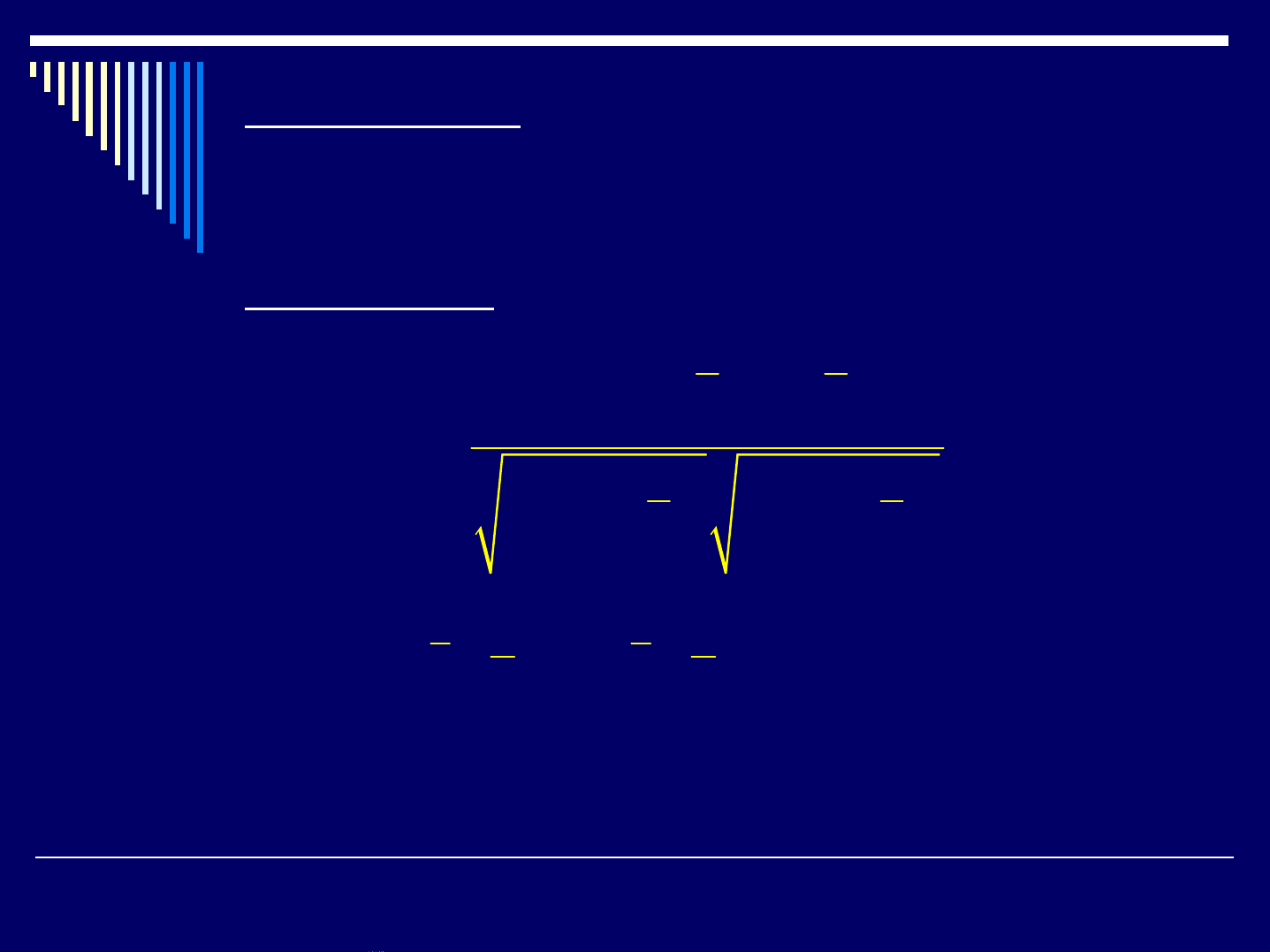
Bước thứhai: Tính hệsố tương quan mẫu
trong đó.
Nếu lớn thì ta phỏng đoán giữa Xvà Ycó quan
hệtuyến tính chặt chẽ.
=
==
−−
=
−−
∑
∑∑
1
22
11
()()
()()
n
ii
i
nn
ii
ii
xxyy
r
x
xyy
==
==
∑
∑
11
11
;
nn
ii
ii
x
xy y
nn
Nếu lớn thì ta phỏng đoán giữa Xvà Ycó quan
hệtuyến tính chặt chẽ.
II. Phương trình hồi qui tuyến tính :
Ta xét trường hợp Xkhông ngẫu nhiên, với X
ngẫu nhiên kết quảcũng tương tự. Xét mẫu lý
thuyết .
Giảsử,
1) Yvà Xcó quan hệtuyến tính và được biểu diễn
bởi phương trình được gọi là mô hình hồi qui tuyến
tính đơn của Ytheo X, trong đóavà blà các hệsố
chưa biết.
2) là các sai sốngẫu nhiên độc lập.
r
=
++ =, 1,....,
ii i
Yaxbei n
1,..., n
ee
11 2 2
( , ), ( , ), ... , ( , )
nn
x
YxY xY