CH NG 9: ƯƠ Ho ch đ nh bàng chuong trinh đ ngạ ị ộ
Trong ch ng này chúng ta quan tâm đ n tr ng h p đ c bi t: toàn b s s n ph m t pươ ế ườ ợ ặ ệ ộ ố ả ẩ ậ
h p trong ch m t h . Trong tr ng h p này, có th c tính tr c ti p giá thành s n xu t ho cợ ỉ ộ ọ ườ ợ ể ướ ự ế ả ấ ặ
t n kho cua 1 sô x, san phâm dua vào trung bình s n xu t c n thi t. Cac ràng bu c truoc dây nhồ ả ấ ầ ế ộ ư
s gi b sung, s th u l i vv....duoc ngâm tinh chung trong gia.ố ờ ổ ự ầ ạ
9.1 Thu t toán cho tr ng h p tông quatậ ườ ợ
9.1.1 Ví d : ụ
Xí nghi p AKL là m t công ty con c a m t nhà xây d ng hàng không l n. Nó lapệ ộ ủ ộ ự ớ
rap và ki m tra nh ng modun đi n t s d ng trong thiêt bi diêu khiên máy bay. Vìể ữ ệ ử ử ụ
nh ng lý do g n v i giá thành, s n xu t có th t 10 đ n 16 thi t b . Cũng v y, vi phaiữ ắ ớ ả ấ ể ừ ế ế ị ậ
co 1 luong hàng t n kho an toàn và do kích c cua kho, sô luong này n m trong kho ngồ ỡ ằ ả
tù 3 dên 6. Không đ c phép thi u h t.ượ ế ụ
Yêu c u trong 6 tháng t i là: 9 17 14 18 11 17 thi t b . Nêu tính s gi b sung và cóầ ớ ế ị ố ờ ổ
th goi thêm 1 công ty gia công, thi chi phí s n xu t CF(x) c a x thi t b (ngoài trù giaể ả ấ ủ ế ị
nguyên vât liêu và linh kiên) là:
x 10 11 12 13 14 15 16
CF(x) 20 22 25 30 33 37 40
Chi phí t n kho hàng tháng làồ
x 3 4 5 6
CS(x) 2 3 5 7
S hàng t n kho ban đ u là 3 đ n v và ng i ta dinh se dat s hàng t n kho cu iố ồ ầ ơ ị ườ ố ồ ố
kỳ th 6 là 4.ứ
Chung ta phai xac dinh sô luong Xi thi t b cân s n xu t trong tháng th i và voi mucế ị ả ấ ứ
tiêu là t i thi u hoa t ng s chi phí s n xu t và chi phí t n kho. đây, nh n th y s quanố ể ổ ố ả ấ ồ Ở ậ ấ ự
tr ng c a vi c s n xu t, không th x p x k t qu b ng m t s th c mà chúng ta pháiọ ủ ệ ả ấ ể ấ ỉ ế ả ằ ộ ố ự
làm vi c b ng nh ng s nguyên. Nh trong ch ng tr c, chúng ta thêệ ằ ữ ố ư ươ ướ m các bi n Si làế
m c t n kho vào cu i tháng i. Ta th y d dàng:ứ ồ ố ấ ễ
Min
6
1
[CF(Xi) + CS(Si)]
i=
∑
V i nh ng ràng bu c:ớ ữ ộ
10 ≤ Xi ≤ 16
3 ≤ Si ≤ 6
S0 = 3
S6 = 4
X1 + S0 = S1 + 9
X2 + S1 = S2 + 17
X3 + S2 = S3 + 14
X4 + S3 = S4 + 18
X5 + S4 = S5 + 11
X6 + S5 = S6 + 17
9.1.2 Mô hình hoá
CF(x) và CS(x) là chi phí s n xu t và t n kho cua x s n ph m. Chi phí t n khoả ấ ồ ả ẩ ồ
đ c tính toán d a trên s hàng t n kho vào cu i kỳ, nh trong các ch ng tr c (cacượ ự ố ồ ố ư ươ ướ
mô hinh se r t ít khác nhau nêu ta gi thi t r ng chi phí đ c tính d a ấ ả ế ằ ượ ự trên s t n khoố ồ
đ u tháng). S luong s n ph m s n xu t có th ch p nh n là gi a XMin và XMax vàầ ố ả ẩ ả ấ ể ấ ậ ở ữ
thêm cac ràng buôc vê sô luong hàng t n kho an toàn hay vê diên tich m t b ng kho nênồ ặ ằ
m c hàng t n kho n m gi a SMin và SMax. Ng i ta bi t đ c s hàng yêu c u c a pứ ồ ằ ữ ườ ế ượ ố ầ ủ
thoi kỳ ti p theo và. dếi là yêu c u c a thoi kỳ th i. M c hàng t n kho đ u tiên là SInit vàầ ủ ứ ứ ồ ầ
ng i ta du đ nh đat s hàng t n kho SFin cu i kỳ th p. Không đ c phép thi u h t.ườ ị ố ồ ở ố ứ ượ ế ụ
Muc đích là xác đ nh đ c s hàng s n xu t Xi kỳ th i đ c c ti u t ng chi phíị ượ ố ả ấ ở ứ ể ự ể ổ
c a s n xu t và t n kho. Chúng ta đ a vào các bi n Si nh tr c, là s thành ph m t nủ ả ấ ồ ư ế ư ướ ố ẩ ồ
kho cu i tháng. Ng i ta thu đ c mô hình sau:ở ố ườ ượ
Min ∑i =1→p[CF(Xi) + CS(Si)]
Và nh ng ràng bu c:ữ ộ
XMin ≤ Xi ≤ XMax
SMin ≤ Si ≤ SMax
S0 = SInit
Sp = SFin
Xi + Si-1 = Si +di
Công th c trên h u nh là công th c đ t đ c trong ch ng tr c. Nh ng đây,ứ ầ ư ứ ạ ượ ươ ướ ư ở
n u nh ng r ng bu c là tuy n tính, hàm m c tiêu không còn n a. Bài toán này khôngế ữ ằ ộ ế ụ ữ
th giai bàng quy ho ch tuy n tính.ể ạ ế
9.1.3 Mô hình hoá d i d ng đ thướ ạ ồ ị
Đ gi i quy t bài toán này, tr c tiên ng i ta s mô hình hoá no d i d ng để ả ế ướ ườ ẽ ướ ạ ồ
th , mà chúng ta s đ nh nghĩa nh ng đ nh và cung.ị ẽ ị ữ ỉ
1. Đ nhỉ
M t đ nh Vộ ỉ i,l bi u th s luong t n kho m c l o cu i kỳ th i.ể ị ố ồ ở ứ ố ứ
2. Cung
Ng i ta t o ra m t cung t Vườ ạ ộ ừ i-1,k đ n Vếi,l nêu co thê di tù tinh trang « s t n khoố ồ
cu i kỳ th i-1 o m c kở ố ứ ứ » dên tinh trang « s t n kho cu i kỳ th i o m c lố ồ ở ố ứ ứ ». Yêu
câu kỳ th i đã bi t là dở ứ ế i, ta suy ra s s n ph m c n s n xu t trong kỳ th i là Xố ả ẩ ầ ả ấ ứ i = l +
di – k.
V i giá tr s t n kho l da duoc biet cu i kỳ th i, cac gi i h n cua Xi s danớ ị ố ồ ở ố ứ ớ ạ ẽ
dên nhung gi i h n vê s t n kho k kỳ th i -1.ớ ạ ố ồ ở ứ
1. Voi s luong tôn kho nh nh t là Xmin.thi giá tr l n nh t c a k đ t đ cố ỏ ấ ị ớ ấ ủ ạ ượ
trong thoi ky i-1 là l + di – XMin.
2. Voi s luong s n xuât l n nh t là Xmax.thi giá tr nh nh t c a k đ t đ c làố ả ớ ấ ị ỏ ấ ủ ạ ượ
l + di – XMax.
M t khác, s t n kho n m trong kho ng t SMin đ n SMax, suy ra k n m trongặ ố ồ ằ ả ừ ế ằ
kho ng kmin và kmax v i ả ớ
kmin = Max (l + di – XMax , SMin)
kmax = Min (l + di – XMax, SMax)
Đ th là m t đ ngồ ị ộ ườ không khep kin. Chúng ta s tìm m t con đ ng ng n nh tẽ ộ ườ ắ ấ
t Vừ0,Sinit đ n Vếp,SFin. Đ th co cac dinh cua tùng thoi ky và voi thoi ky i duoc dinh boiồ ị
luong tôn kho tang. Thu t toán chung:ậ
Voi i thay doi t 1 đ n pừ ế
Voi l thay doi t SMin đ n SMax ừ ế
Chiphí(Vi,l) = ∞
Kỳ th nh t ứ ấ
Voi l thay doi t SMin đ n SMax ừ ế
kmin = Max (l + di – XMax , SInit)
kmax = Min (l + di – XMin, SInit)
N u kmin = kmax thì ế
Chiphí(V1,l) = CS(l) + CF(l+di - SInit)
k t thúc.ế
Kỳ th 2 đ n kỳ th pứ ế ứ
Voi i thay doi t 2 đ n p ừ ế
Voi l thay doi t SMin đ n SMax ừ ế
kmin = Max (l + di – XMax , SMin)
kmax = Min (l + di – XMin, SMax)
Voi k thay doi t kmin đ n kmax ừ ế
C= CS(l) + Chiphí(Vi-1,k) + CF(l + di – k)
N u Chiphí(Viế,l) > C thì Chiphí(Vi,l) =C
K t thúcế
K t thúcế
Dây là tr ng h p đ c bi t c a ườ ợ ặ ệ ủ chuong trinh đ ngộ.
9.1.4 Dap an
Vi,l KMin KMax Xi Chiphí Vi-1,k
( 1, 3 )
( 1, 4 )
( 1, 5 )
( 1, 6 )
3
3
3
3
2
3
3
3
10
11
12
∞
22
24
27
( 0, 3 )
( 0, 3 )
( 0, 3 )
( 2, 3 )
( 2, 4 )
( 2, 5 )
( 2, 6 )
4
5
6
7
6
6
6
6
16
16
16
65
69
74
∞
( 1, 4 )
( 1, 5 )
( 1, 6 )
( 3, 3 )
( 3, 4 )
( 3, 5 )
( 3, 6 )
3
3
3
4
6
6
6
6
14
15
16
16
100
104
107
112
( 2, 3 )
( 2, 3 )
( 2, 3 )
( 2, 4 )
( 4, 3 )
( 4, 4 )
( 4, 5 )
( 4, 6 )
5
6
7
8
6
6
6
6
16
16
152
159
∞
∞
( 3, 5 )
( 3, 6 )
( 5, 3 )
( 5, 4 )
( 5, 5 )
( 5, 6 )
3
3
3
3
4
5
6
6
11
12
13
14
176
179
184
187
( 4, 3 )
( 4, 3 )
( 4, 3 )
( 4, 3 )
( 6, 3 )
( 6, 4 )
( 6, 5 )
( 6, 6 )
4
5
6
7
6
6
6
6
16
16
16
222
229
234
∞
( 5, 4 )
( 5, 5 )
( 5, 6 )
B ng 9.1 - B ng k t quả ả ế ả
B ng 9.1 đ a ra k t qu c a thu t toán áp d ng cho ví d trên . Dê có 4 s nả ư ế ả ủ ậ ụ ụ ả
ph m t n kho cu i kỳ 6, chi phí t i u là 229. Do trên bang 9.1 ta duoc lô trinh tôi uuẩ ồ ở ố ố ư
cho boi các dinh:
( 6, 4 ), ( 5, 5 ), ( 4, 3 ), ( 3, 5 ), ( 2, 3 ), ( 1, 4 )
K ho ch s n xu t trên 6 kỳ se là : ( 10, 16, 16, 16, 13, 16 )ế ạ ả ấ
9.2 Thu t toán trong tr ng h p lõmậ ườ ợ
9.2.1 Đ nh nghĩaị
Thu t ậtoán tông quat có thể được đơn giản hoá khi cac chi
phí CF và CS đều là lõm. Voi F(x) là một hàm không liên tục
(rời rạc) và đặt f(x) = F(x) – F(x-1). Hàm f(x) biểu diễn
l ng tăng c a F, khi ng i ta đi t x-1 đ n x.. Khi F(x) bi u th m t hàm chi phí, f(x)ượ ủ ườ ừ ế ể ị ộ
đ c hi u nh là chi phí gi i h n dê s n xu t s n ph m th x. N u f(x) ≤ f(x-1), hàmượ ể ư ớ ạ ả ấ ả ẩ ứ ế
F(x) đ c g i là lõm. đây chi phí gi i h n gi m d n. ượ ọ Ở ớ ạ ả ầ Ng i ta goi là kinh tê do quyườ
mô. Đó là tr ng h p cac nên s n xu t có chi phi cô dinh rât cao hoac dôc lâp voi sôườ ợ ả ấ
luong s n xu t.ả ấ
N u f(x) ≥ f(x+1), hàm F(x) đ c g i là lôi. ế ượ ọ Chi phí gi i h n tăng lên.ớ ạ
Tr ng h p này x y ra khi ng i ta phai, v t qua 1 ng ng s n xu t nào do,ườ ợ ả ườ ượ ưỡ ả ấ
c n đ n nh ng phuong tiên b sung, nh nh ng gi b sung ho c qua gia công.ầ ế ữ ổ ư ữ ờ ổ ặ
9.2.2 Mô hình hoá
Nhu trong truong hop tr c, và thêm vào m t s gia thiêt b sung sau:ướ ộ ố ổ
1. Các hàm chi phí CF và CS là lõm.
2. Không có gi i h n v kh năng s n xu t cũng nh kh năng t n kho.ớ ạ ề ả ả ấ ư ả ồ
D a trên nh ng đi u ki n đó, chúng ta có đ nh lý c a Wagner và Within d iự ữ ề ệ ị ủ ướ
đây:
Trong nh ng gi i pháp t i u, luôn t n t i m t 1 giai phap mà viêc s n xu t Xiữ ả ố ư ồ ạ ộ ả ấ
(s l ng s n ph m s n xu t ra trong kỳ th i) tho :ố ượ ả ẩ ả ấ ứ ả
● ho c b ng 0,ặ ằ
● ho c b ng t ng s s n ph m đ c yêu c u trong kỳ th i và k kỳ ti p theo:ặ ằ ổ ố ả ẩ ượ ầ ứ ế
Xi = di + ... + di+k, voi k ≥ 0.
Ch ng minh:ứ
Xét m t gi i pháp t i u S kỳ th i mà s s n ph m s n xu t là Xi b ng t ngộ ả ố ư ở ứ ố ả ẩ ả ấ ằ ổ
các giá tr dịi, di+1, ... , di+k-1, và m t ph n c a dộ ầ ủ i+k. C(S) là chi phí c a gi i pháp đó. Xétủ ả
hai gi i pháp co thê th c hi n sau dây:ả ự ệ
1.
+
S
: Ng i ta s n xu t nhi u h n m t s n ph m trong kỳ i và ít h n m t s nườ ả ấ ề ơ ộ ả ẩ ơ ộ ả
ph m trong kỳ th k. Chi phí s n xu t trong kỳ th i tăng lên là ẩ ứ ả ấ ứ
+
a
= f(Xi + 1), chi phí
t n kho tăng lên là ồ
+
b
, và chi phí s n xu t trong kỳ i + k gi m đi m t l ng ả ấ ả ộ ượ
+
c
= f(Xi +k)
2. S‾ : Ng i ta s n xu t ít h n m t s n ph m trong kỳ th i và nhi u h n m tườ ả ấ ơ ộ ả ẩ ứ ề ơ ộ
s n ph m trong kỳ th k. Chi phí s n xu t trong kỳ th i gi m đi là a‾ = f(Xả ẩ ứ ả ấ ứ ả i), chi phí
t n kho gi m đi là b‾ , và chi phí s n xu t trong kỳ i + k tăng lên m t l ng c‾ = f(Xồ ả ả ấ ộ ượ i +k
+ 1).
Gi đ nh ả ị
+
S
không ph i là t i u; do S là t i u ta có:ả ố ư ố ư
C(S) < C(
+
S
) = C(S) +
+
a
+
+
b
–
+
c
C(S) ≤ C(S‾ ) = C(S) – a‾ – b‾ + c‾
Hay
0 <
+
a
+
+
b
–
+
c
a‾ + b‾ – c‾ ≤ 0
Suy ra :
+
a
+
+
b
–
+
c
> a‾ + b‾ – c‾
Do các hàm là lõm, nên
+
a
≤ a‾
+
b
≤ b‾
–
+
c
≤ – c‾
Và nh v y ư ậ
+
a
+
+
b
–
+
c
≤ a‾ + b‾ – c‾ Ph n ch ng l i ph ng trình tr c ả ứ ạ ươ ướ
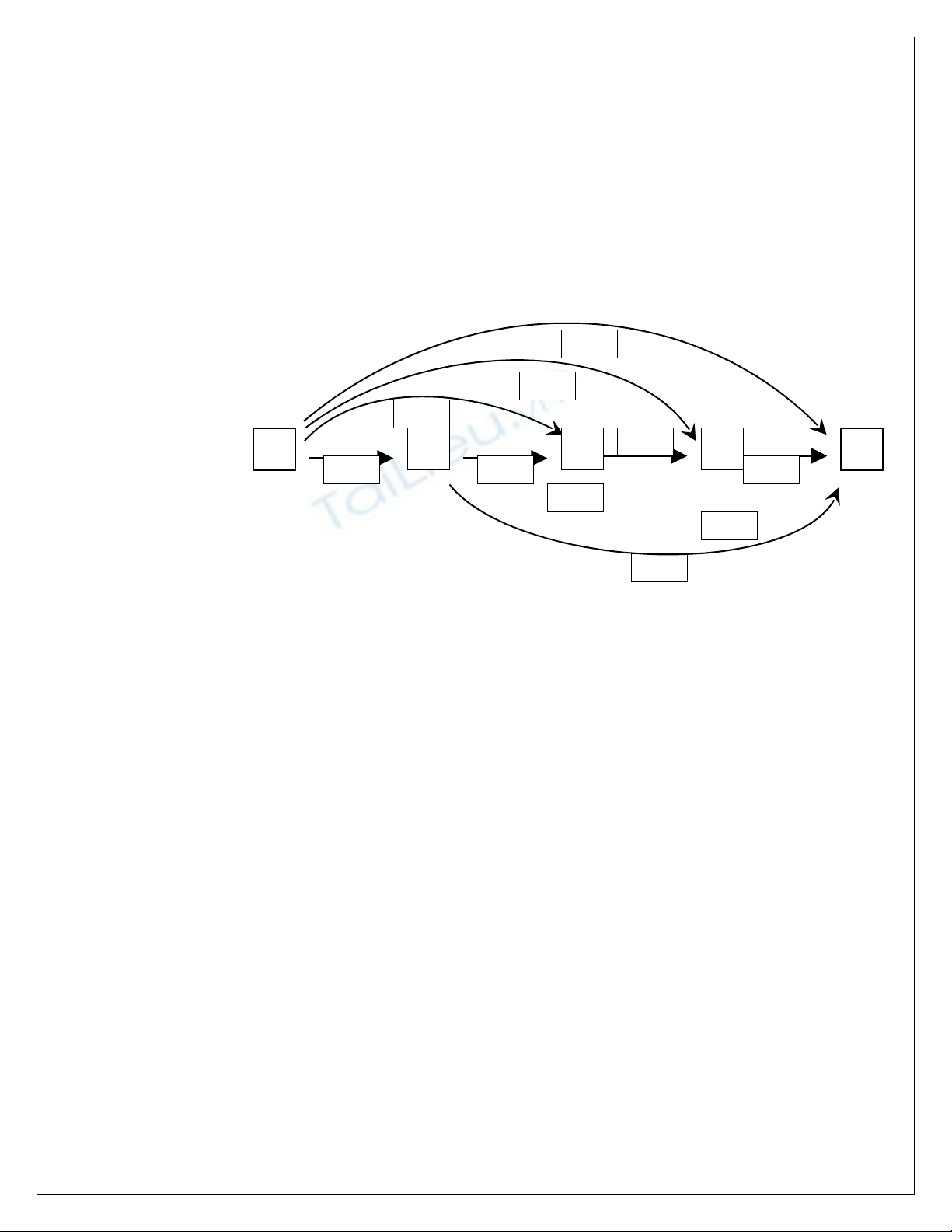
9.2.3 Mô hình hoá d i d ng đ thướ ạ ồ ị
Vây chi cân han chê vi c tìm ki m gi i pháp cho gi thi t nói trên. Gi thi t nàyệ ế ả ả ế ả ế
có th đ c mô hình hoá d i d ng s đ mà trong đó các đ nh và các cung đ nh nghĩaể ượ ướ ạ ơ ồ ỉ ị
nh sau:ư
1. Đ nh: M t đ nh Vỉ ộ ỉ i bi u th vi c b trí s n xu t trong kỳ th i. D nh Vể ị ệ ố ả ấ ứ ỉ p+1 duoc
thêm vào dê gi i h n ph m vi lâp kê ho ch.ớ ạ ạ ạ
2 3
852
562
208 272
148
344
576
1
4 5
466
216
322