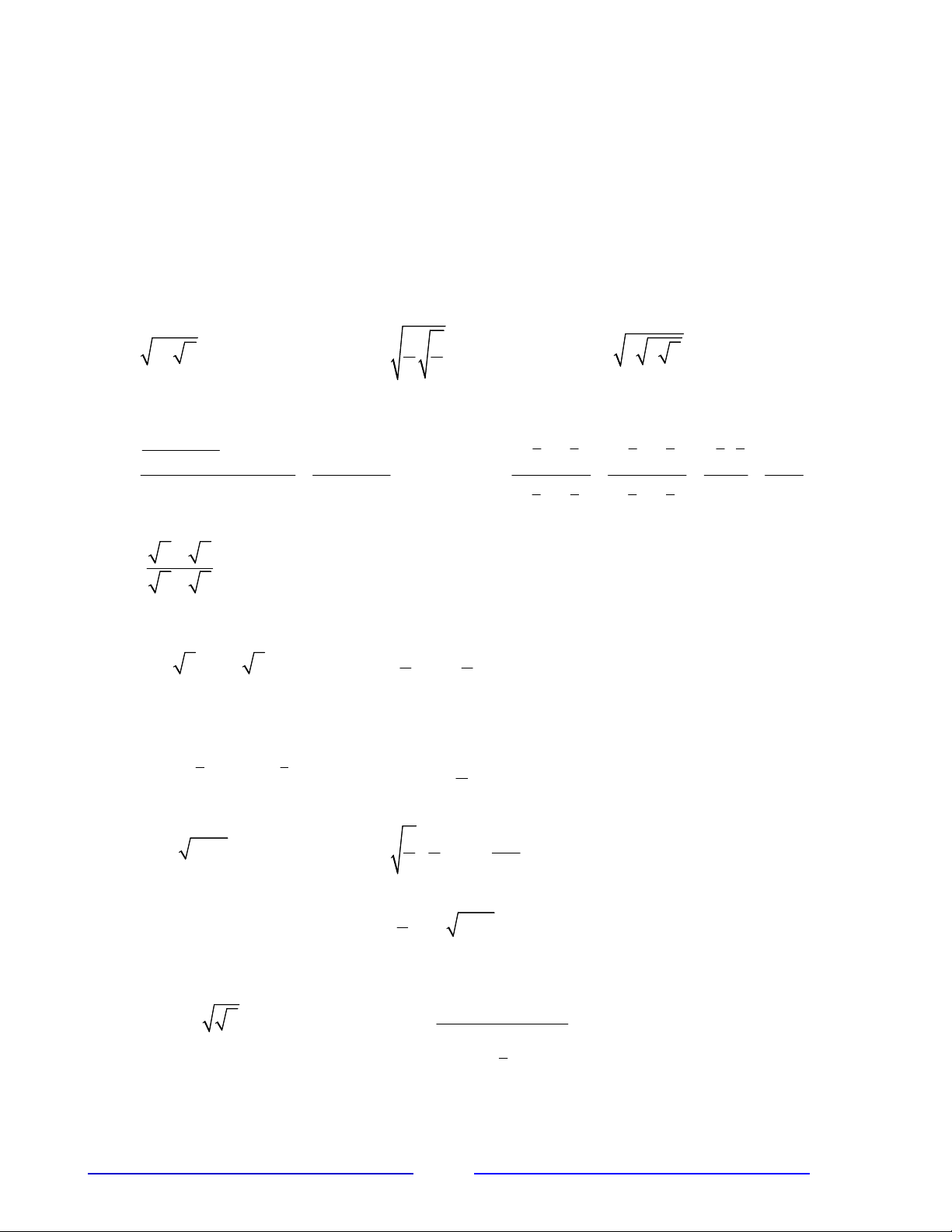
https://www.facebook.com/letrungkienmath https://sites.google.com/site/letrungkienmath
CHUYÊN ĐỀ II:
HÀM SỐ LŨY THỪA, HÀM SỐ MŨ, HÀM SỐ LÔGARIT
Chủ đề 2.1:Lũy thừa, mũ, logarit
A. Bài tập luyện tập
Bài 1 Viết các biểu thức sau dưới dạng lũy thừa
a)
423
, 0
x x x b)
53
, , 0
b a a b
a b
c) 53
2 2 2
Bài 2 Tìm điều kiện và rút gọn các biểu thức sau
a)
1,5 1,5 0,5 0,5 0,5
0,5 0,5
0,5 0,5
2
a b a b b
a b
a b
a b
b)
1 1 1 1 3 1
2 2 2 2 2 2
1 1 1 1
2 2 2 2
.
x y x y x y y
x y x y
xy x y xy x y
c)
3 3
6 6
a b
a b
(a,b>0 , a ≠ b)
Bài 3 So sánh m và n
a)
2 2
m n
b)
1 1
9 9
m n
Bài 4 Tìm điều kiện của a và x biết
a)
2 1
3 3
1 1
a a
b)
0,2
2
1
a
a
c) 5
4 1024
x d)
1
5 2 8
2 5 125
x
e)
0,1 100
x f) 3
1
0,04
5
x
Bài 5. Rút gọn biểu thức :
a) 3
loga
a
(a > 0) b ) 3 4
1/3
7
1
log .log
log
a a
a
a a
a (
0 1
a
)
Bài 6: Tính giá trị biểu thức logarit theo các biểu thức đã cho :
https://www.facebook.com/letrungkienmath https://sites.google.com/site/letrungkienmath
a) Cho 2
log 14
a
. Tính 49
log 32
theo a.
b) Cho 15
log 3
a
. Tính 25
log 15
theo a.
a) Cho 25
log 7
a
; 2
log 5
b
. Tính 35
49
log
8
theo a, b.
b) Cho 30
log 3
a
; 30
log 5
b
. Tính 30
log 1350
theo a, b.
Bài 7: Chứng minh các biểu thức sau (với giả thuyết các biểu thức đều có nghĩa ) :
a)
log log
a a
c b
b c b)
log log
log ( ) 1 log
a a
ax
a
b x
bx
x
c) 1
log (log log )
3 2
c c c
a b
a b
, với 2 2
7
a b ab
.
B. Bài tập TNKQ
Câu 1: Cho a > 0 và a 1. Tìm mệnh đề đúng trong các mệnh đề sau :
A. a
log x
có nghĩa x B. loga1 = a và logaa = 0
C. logaxy = logax.logay D. n
a a
log x n log x
(x > 0,n 0)
Câu 2: Cho a > 0 và a 1, x và y là hai số dương . Tìm mệnh đề đúng trong các mệnh đề sau :
A. a
a
a
log x
x
log
y log y
B. a
a
1 1
log
x log x
C.
a a a
log x y log x log y
D. b b a
log x log a.log x
Câu 3: 3
7
1
a
log a
(a > 0, a 1) bằng :
A. -
7
3
B.
2
3
C.
5
3
D. 4
câu 4 :
3 5
2 2 4
a15 7
a a a
log
a
bằng :
A. 3 B.
12
5
C.
9
5
D. 2
Câu 5:
a
3 2log b
a
(a > 0, a 1, b > 0) bằng :
https://www.facebook.com/letrungkienmath https://sites.google.com/site/letrungkienmath
A.
3 2
a b
B.
3
a b
C.
2 3
a b
D.
2
ab
Câu 6 : Nếu a a a a
1
log x log 9 log 5 log 2
2
(a > 0, a 1) thì x bằng :
A.
2
5
B.
3
5
C.
6
5
D. 3
Câu 7: Nếu 2 2 2
log x 5 log a 4 log b
(a, b > 0) thì x bằng :
A.
5 4
a b
B.
4 5
a b
C. 5a + 4b D. 4a + 5b
Câu 8 : nếu
2 3
7 7 7
log x 8log ab 2 log a b
(a, b > 0) thì x bằng :
A.
4 6
a b
B.
2 14
a b
C.
6 12
a b
D.
8 14
a b
Câu 9: Cho log2 = a. Tính log25 theo a?
A. 2 + a B. 2(2 + 3a) C. 2(1 - a) D. 3(5 - 2a)
Câu 10 : Cho log 2 3
5 a; log 5 b
. Khi đó 6
log 5
tính theo a và b là :
A.
1
a b
B.
ab
a b
C. a + b D.
2 2
a b
Câu 11 : Cho hai số thực dương
a
và
,
b
với
1.
a
Khẳng định nào dưới đây là khẳng định đúng ?
A.
2
1
log log .
2
a
a
ab b
B.
2
1
log log .
4
a
a
ab b
C.
log 2 2log .
2
ab b
a
a D.
2
1 1
log log .
2 2
a
a
ab b
Câu 12. Cho
log 2
a
. Tính
32
4
log
5
theo a, ta được:
A.
1
6
1
4a
. B.
1
5 1
4
a
. C.
1
6 1
4
a
. D.
1
6 1
4
a
.
Câu 13. Rút gọn biểu thức 2log 2
3
3 log .log 25 (0 1)
5
a
P a a
a
, ta được:
A. 2
4
P a
. B. 2
2
P a
. C. 2
4
P a
. D. 2
2
P a
.
Câu 14: Cho a là một số dương, biểu thức
2
3
a a
viết dưới dạng luỹ thừa với số mũ hữu tỷ là:
A.
7
6
a
B.
5
6
a
C.
6
5
a
D.
11
6
a
Câu 15: Biểu thức a
4
3
2
3
: a
viết dưới dạng luỹ thừa với số mũ hữu tỷ là:
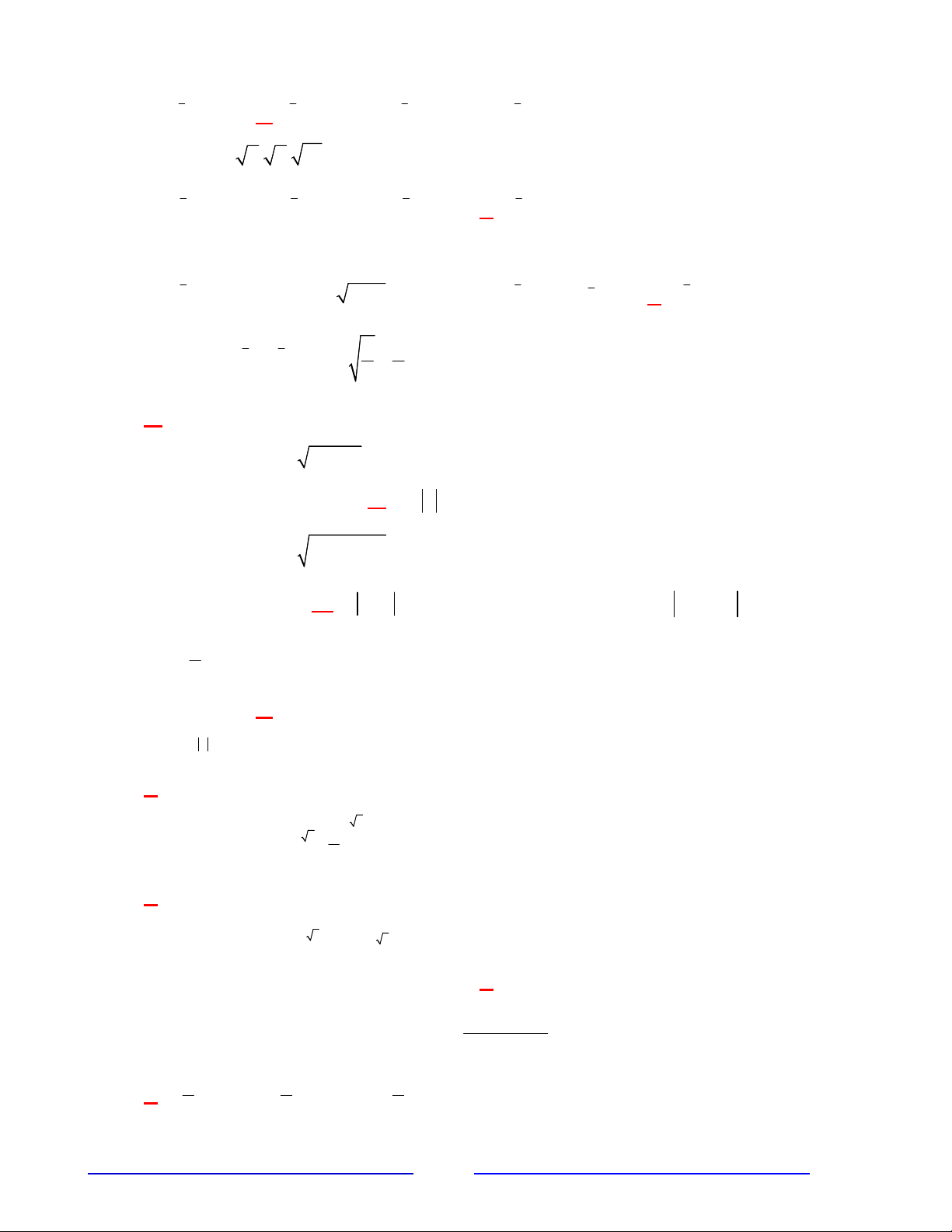
https://www.facebook.com/letrungkienmath https://sites.google.com/site/letrungkienmath
A.
5
3
a
B.
2
3
a
C.
5
8
a
D.
7
3
a
Câu 16: Biểu thức 6
5
3
x. x. x
(x > 0) viết dưới dạng luỹ thừa với số mũ hữu tỷ là:
A.
7
3
x
B.
5
2
x
C.
2
3
x
D.
5
3
x
Câu17: Trong các phương trình sau đây, phương trình nào có nghiệm?
A.
1
6
x
+ 1 = 0 B.
x 4 5 0
C.
11
56
x x 1 0
D.
1
4
x 1 0
Câu18: Cho K =
1
2
1 1
2 2
y y
x y 1 2
x x
. biểu thức rút gọn của K là:
A. x B. 2x C. x + 1 D. x - 1
Câu19: Rút gọn biểu thức:
4 2
81a b
, ta được:
A. 9a2b B. -9a2b C. 2
9a b
D. Kết quả khác
Câu20: Rút gọn biểu thức:
4
8
4
x x 1
, ta được:
A. x4(x + 1) B. 2
x x 1
C. -
2
4
x x 1
D.
x x 1
Câu21: Nếu
1
a a 1
2
thì giá trị của là:
A. 3 B. 2 C. 1 D. 0
Câu22: Cho
3 27
. Mệnh đề nào sau đây là đúng?
A. -3 < < 3 B. > 3 C. < 3 D. R
Câu23: Rút gọn biểu thức
2 1
21
aa
(a > 0), ta được:
A. a B. 2a C. 3a D. 4a
Câu24: Rút gọn biểu thức
2
3 1
2 3
b : b
(b > 0), ta được:
A. b B. b2 C. b3 D. b4
Câu25: Cho x x
9 9 23
. Khi đo biểu thức K =
x x
x x
5 3 3
1 3 3
có giá trị bằng:
A.
5
2
B.
1
2
C.
3
2
D. 2
https://www.facebook.com/letrungkienmath https://sites.google.com/site/letrungkienmath
Chuyên đề 2: HÀM SỐ LŨY THỪA HÀM SỐ MŨ
Chủ đề 2.2: Hàm số lũy thừa, mũ, logarit
A. Bài tập luyện tập
Bài 1: Tìm đạo hàm của các hàm số sau:
a, y= e3x b, y=2x c, y= 2
1
3x
HD:
a,(e3x)’ = e3x.(3x)’ = 3e3x
b, (2x)’ = 2x.ln2;
c,( 2
1
3x)’ = 2
1
3x.(ln3). (1-x2)’ = -2x. 2
1
3x.ln3
Bài 2: Tìm TXĐ của các hàm số sau:
a, y = x3 b, y = x -3 c, y = 3
2
x d, y = 2
x
HD:
a, y = x3 có D = R (vì
= 3 nguyên dương)
b, y = x -3 có D = R\{0} (vì
= - 3 nguyên âm)
c, y = 3
2
x(
hữu tỉ);
d, y = 2
x (
vô tỉ) nên có D = R+ = (0;+
)
Bài 3: Tìm đạo hàm của các hàm số sau:
a, y=
3
4
x
(x>0) b, y= 32
1x (
1 1
x
)
HD:
+ 1
4
3
4
3
4
3
)'(
xx =4
1
4
3
x=
4
1
4
3
x
= 4
4
3
x