
Chuyên đề
ĐỒ THỊ
HAMILTON

Khái ni m đ ng đi Hamilton đ c xu t ệ ườ ượ ấ
phát t bài toán:ừ
“Xu t phát t m t đ nh c a kh i th p ấ ừ ộ ỉ ủ ố ậ
nh di n đ u, hãy đi d c theo các c nh ị ệ ề ọ ạ
c a kh i đó sao cho đi qua t t c các ủ ố ấ ả
đ nhkhác, m i đ nh đi qua đúng m t l n, ỉ ỗ ỉ ộ ầ
sau đó tr v đ nh xu t phát”ở ề ỉ ấ
Bài toán này đ c nhà toán h c Hamilton ượ ọ
đ a ra vào năm 1859ư
Giới thiệu:
Nhà toán học Hamilton
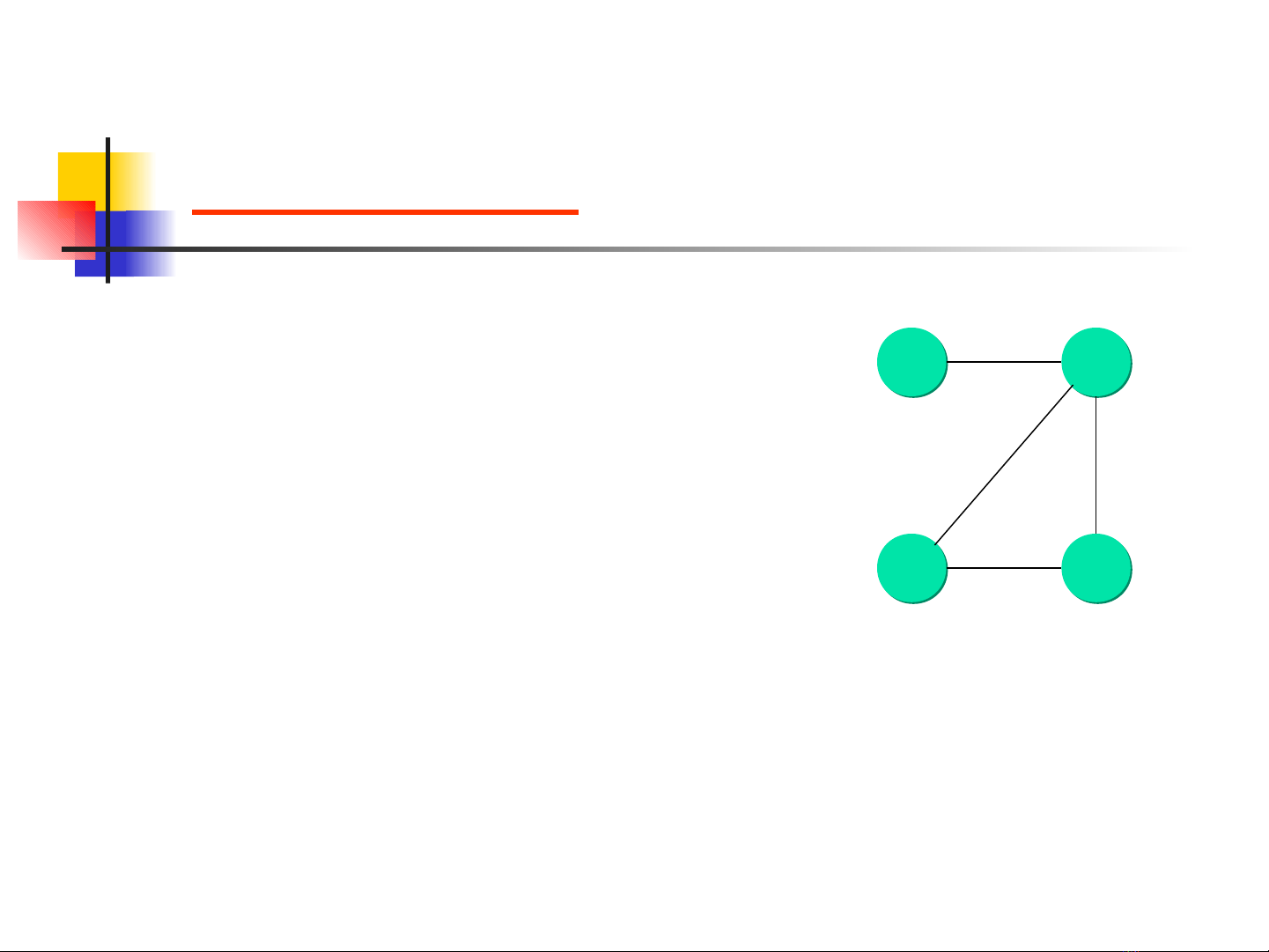
• Đ ng đi Hamiltonườ là đ ng qua ườ
t t c các đ nh c a đ th và đi qua ấ ả ỉ ủ ồ ị
m i đ nh đúng m t l nỗ ỉ ộ ầ
Hay đ ng đi (x[1],x[2],…,x[n]) ườ
đ c g i là đ ng đi Hamilton ượ ọ ườ
n u x[i]ế≠x[j] (1≤i<j≤n)
Định nghĩa:
a
d
b
c
G2
Ví dụ: Đường đi Hamilton của đồ thị G2 là: a b c d
Định nghĩa:
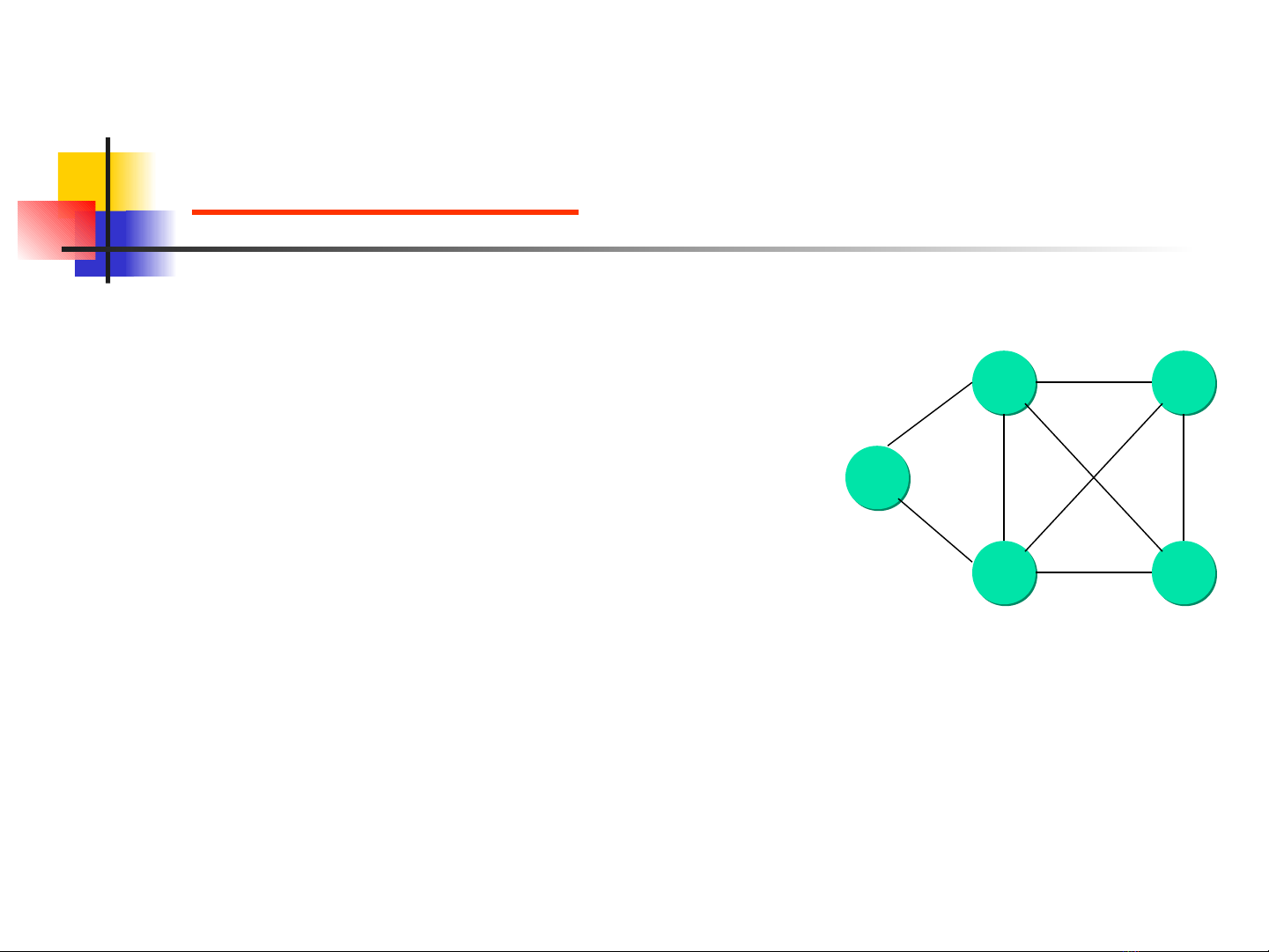
• Chu trình Hamilton là đ ng đi ườ
Hamilton có m t c nh trong đ th n i ộ ạ ồ ị ố
đ nh đ u v i đ nh cu i c a đ ng điỉ ầ ớ ỉ ố ủ ườ
Hay chu trình (x[1],x[2],…,x[n],x[1])
đ c g i là chu trình Hamilton n u ượ ọ ế
x[i]≠x[j] (1≤i<j≤n)
a
b
e
c
d
G1
Ví dụ: Chu trình Hamilton của đồ thị G1 là: a b c d e a

• Đ th Hamilton là đ th có ch a m t chu ồ ị ồ ị ứ ộ
trình Hamilton
• Đ th n a Hamilton là đ th có ch a m t ồ ị ử ồ ị ứ ộ
đ ng đi Hamiltonườ
Định nghĩa:


















![Giáo trình Giải tích hàm một biến 1: Phần 2 [Full Nội Dung]](https://cdn.tailieu.vn/images/document/thumbnail/2026/20260127/hoatulip0906/135x160/60731769587731.jpg)
![Giáo trình Giải tích hàm một biến 1: Phần 1 [Full]](https://cdn.tailieu.vn/images/document/thumbnail/2026/20260127/hoatulip0906/135x160/70271769587732.jpg)



![Bài tập Toán cao cấp (HP1) [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2026/20260127/hoahongcam0906/135x160/69221769507713.jpg)


