Cơ sở Hóa lý
cho Mô phỏng
Mục lục
Phần 1. Động hóa học ............................................................................................... 1
Khái niệm về động hóa học ......................................................................... 1
Tính toán tốc độ phản ứng với các bậc khác nhau ....................................... 1
1.2.1. Phản ứng bậc 0 ........................................................................................ 1
1.2.2 Phản ứng bậc 1 ......................................................................................... 2
1.2.3 Phản ứng bậc 2 ......................................................................................... 2
1.2.4 Phản ứng bậc 3 ......................................................................................... 3
1.2.5 Phản ứng bậc n ......................................................................................... 3
1.2.6 Phản ứng thuận nghịch ............................................................................. 4
1.2.7 Phản ứng song song ................................................................................. 5
1.2.8 Phản ứng nối tiếp ..................................................................................... 5
Lý thuyết phản ứng ..................................................................................... 6
1.3.1 Ảnh hưởng của nhiệt độ đến tốc độ phản ứng ........................................... 6
1.3.2 Lý thuyết phản ứng .................................................................................. 7
Phản ứng dị thể ........................................................................................... 8
1.4.1 Cơ chế phản ứng dị thể ............................................................................. 8
1.4.2 Động học của phản ứng xúc tác dị thể .................................................... 10
1.4.3 Phương trình động học tổng quát của phản ứng dị thể ............................ 10
Phần 2. Nhiệt động hóa học .................................................................................... 13
Hai nguyên lý cơ bản của nhiệt động học .................................................. 13
2.1.1. Nguyên lý 1 ........................................................................................... 13
2.1.2. Nguyên lý 2 ........................................................................................... 16
2.1.3. Nguyên lý 3 ........................................................................................... 17
Cân bằng pha ............................................................................................ 17
2.2.1. Điều kiện cân bằng pha ......................................................................... 17
2.2.2. Quy tắc pha Gibbs ................................................................................. 17
2.2.3. Hằng số cân bằng pha............................................................................ 17
Cân bằng hoá học ..................................................................................... 18
Sự chuyển dịch cân bằng - Nguyên lí Le Chatelier .................................... 19
Nhiệt động học các hỗn hợp khí ................................................................ 20
2.5.1 Khí lý tưởng ........................................................................................... 20
2.5.2 Khí thực ................................................................................................. 20
2.5.3 Phương pháp tính toán các đại lượng nhiệt động của khí thực ................ 21
Nhiệt động học và Mô phỏng .................................................................... 21
2.6.1 Các Hệ nhiệt động trong mô phỏng (Property Packages) ........................ 21
2.6.2 Tính cân bằng pha hệ nhiều cấu tử ......................................................... 24
Tài liệu tham khảo .................................................................................................. 35
1
Phần 1. Động hóa học
Khái niệm về động hóa học
Động hóa học nghiên cứu diễn biến của quá trình biến đổi hóa học các chất thể
hiện: cơ chế phản ứng
tốc độ phản ứng
yếu tố ảnh hưởng tới tốc độ phản ứng
(nhiệt độ, áp suất, nồng độ..).
Đại lượng quan trọng nhất của động hóa học là: vận tốc phản ứng (v) và hằng số
tốc độ (k).
Điều kiện để xảy ra phản ứng hóa học:
Điều kiện theo động hóa học:
Theo lý thuyết phản ứng và thực nghiêm các phản ứng hóa học chỉ có thể
xảy ra nếu có va chạm giữa các phân tử với nhau và các va chạm này phải có đủ
năng lượng để vượt qua năng lượng tối thiểu (năng lượng hoạt hóa của phản
ứng) là Ea.
Định luật tác dụng khối lượng:
Là định luật được sử dụng phổ biến nhất trong phần động hóa học. Định
luật nêu rằng:
v = k. Cau.Cbv....
Trong đó: v- là tốc độ của phản ứng.
k- hằng số tốc độ phản ứng.
u,v- bậc của chất tham gia phản ứng A, B...
n= u+ v+ .. là bậc chung của phản ứng.
Tính toán tốc độ phản ứng với các bậc khác nhau
Dựa theo định luật tác dụng khối lượng có thể chia thành các trường hợp sau:
1.2.1. Phản ứng bậc 0
A
B
Tốc độ phản ứng:
v = k=
dC
dt
dC k dt C kt H

2
t = 0 H= -Co
do đó, Co- C = kt
1.2.2 Phản ứng bậc 1
Xét phản ứng: A
B
- Áp dụng định luật tác dụng khối lượng:
v = k. Cu (C- nồng độ của A tại thời điểm t và u= 1).
v= k.C (1)
- Mặt khác, có thể tính tốc độ phản ứng theo công thức sau:
Vận tốc phản ứng bằng biến thiên nồng độ của chất tham gia hoặc là sản phẩm theo
thời gian. Có công thức như sau:
v =
dC
dt
(2)
(biểu thức có dấu - nếu là chất tham gia, không có dấu - khi là sản phẩm)
- Từ (1) và (2):
dC
dt
= k.C
- lnC= kt + H (3)
nếu t= 0 C= Co (nồng độ chất A lúc ban đầu) và H= -lnCo
Do đó, từ biểu thức (3)
ln o
Ckt
C
C= Co. e-kt và k=
1.ln o
C
tC
1.2.3 Phản ứng bậc 2
a. Với nồng độ ban đầu khác nhau
A + B P
t = 0 Co = a b 0
t = t C = ax bx x
v=
dx
dt
= h.(a-x).(b-x)
( ).( )
dx kdt
a x b x

Tiến hành giải tích phân trên ta được:
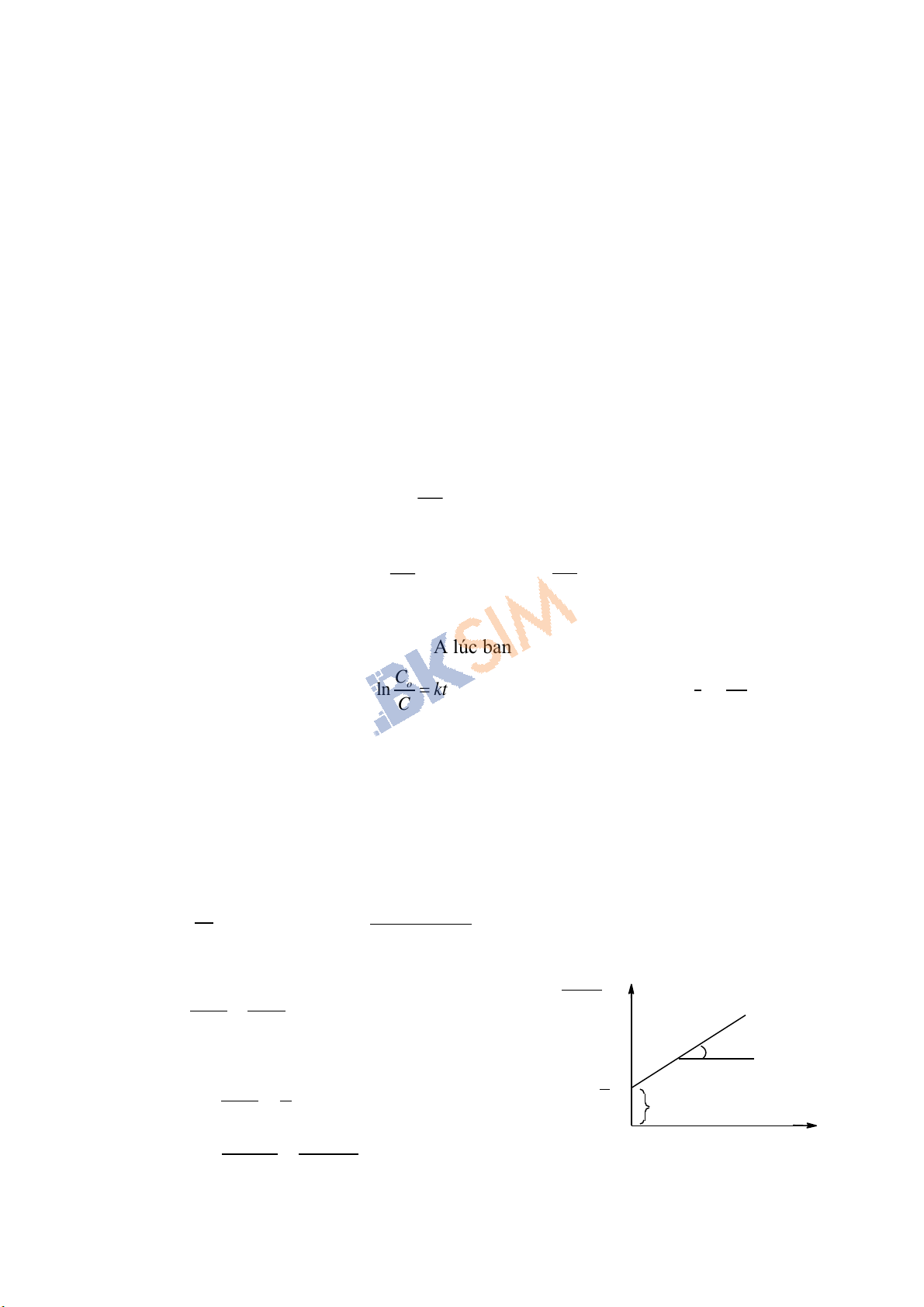
1ln bx kt H
b a a x


t = 0, x= 0
H=
1ln b
b a a
và k =
1 ( )
ln
( ) ( )
a b x
t b a b a x

t
tga = k (b-a)
𝑙𝑛𝑏−𝑥
𝑎−𝑥
−𝑙𝑛𝑎
𝑏