ĐÊ ÔN THI HOC KY II – NĂM HOC 2009 – 2010
MÔN TOAN – L P 10 Ơ
( Th i gian làm bài 90 phút )ờ
Đ SÔ 1Ề
I . PH N CHUNG CHO T T C THÍ SINH (7 đi m ) Ầ Ấ Ả ể
Câu I ( 2,0 đi m ) ể
a) Cho
3
sin 5
= −
α
v i ớ
0
2
− < <
πα
. Tính
os , tanc
α α
.
b) Ch ng minh đăng th c sau : ư ư
1)(cos2
2
coscos
244
−+=
−− xxx
π
π
Câu II ( 2,0 đi m ) ểGi i các ph ng trinh, bât ph ng trinh sau:ả ươ ươ
a)
2 3 3
1
x
x
++
−
b) 2x + = 33 - 3x
Câu III ( 3,0 đi m ) ể
Trong m t ph ng t a đ Oxy cho ba đi m A(1;2), B(3;1), C(5;4).ặ ẳ ọ ộ ể
a) Vi t ph ng trình đ ng th ng BC và đ ng th ng ch a đ ng cao h t A c a tam giácế ươ ườ ẳ ườ ẳ ư ườ ạ ừ ủ
ABC.
b) Tính di n tích tam giác ABC.ệ
c) Vi t ph ng trình đ ng tròn ngo i ti p tam giác ABC.ế ươ ườ ạ ế
II . PH N RIÊNG ( 3 đi m ) Ầ ể
Thí sinh ch đ c làm m t trong hai ph n (ph n 1 ho c ph n 2)ỉ ượ ộ ầ ầ ặ ầ
1.Theo ch ng trình chu n :ươ ẩ
Câu IV.a ( 1,0 đi m ) : ể
Ch ng minh r ng : ư ằ
cosa cos5a 2sina
sin4a sin2a
−=
+
Câu V.a ( 2,0 đi m ) : ể
a) Ch ng minh r ng : ư ằ
(a c)(b d) ab cd+ +c+
b) Cho ph ng trình : ươ
2 2
(m 4)x 2(m 2)x 1 0− + − + =
. Đ nh m đ ph ng trình có hai nghi mị ể ươ ệ
phân bi t ?ệ
2.Theo ch ng trình nâng cao :ươ
Câu IV.b ( 1,0 đi m ) : ể
Tìm giá tr nh nh t và giá tr l n nh t n u có c a hàm s f(x) = sinx + cosx .ị ỏ ấ ị ớ ấ ế ủ ố
Câu V.b ( 2,0 đi m ) : ể
a) Cho
. Tính giá tr c a bi u th c : ị ủ ể ư
1 1
A2 2
sin cos
= +
α α
b) Tìm m đ b t ph ng trình xể ấ ươ 2 + (2m - 1)x + m – 1 < 0 có nghi mệ
1
Đ SÔ 2Ề
I . PH N CHUNG CHO T T C THÍ SINH (7 đi m ) Ầ Ấ Ả ể
Câu 1. (2 đi m) ể
Cho biê th c f(x)= ủ ư
− + +
2
2 3 4m x m x m
a) Xác đ nh t t c các giá tr c a tham s m đ ph ng trình f(x) = 0 có 2 nghi m trái d uị ấ ả ị ủ ố ể ươ ệ ấ
b) Tìm m đ f(x) ể≥ 0, ∀x
Câu 2. (2 đi m)ể
Cho b ng phân b t n s c a m t m u s li u nh sau:ả ố ầ ố ủ ộ ẫ ố ệ ư
i
x
0 2 3 5 6 7 9 1
0
i
n
1 1 4 2 1 2 2 3 N=16
Hãy tìm s trung bình, s trung v , m t c a m u s li u nói trên.ố ố ị ố ủ ẫ ố ệ
Câu 3. (3 đi m) ể
Trong m t ph ng to đ Oxy, cho đi m ặ ẳ ạ ộ ể
( )
1;2I−
và hai đ ng th ng ườ ẳ
1
: 3 0x y∆ + − =
;
2
1
:4
x t
y t
= − +
=
∆∆= +
=
.
a) Vi t ph ng trình đ ng th ng d đi qua I và vuông góc v i ế ươ ườ ẳ ớ
2
∆
.
b) Tìm to đ các đ nh c a tam giác có hai c nh l n l t n m trên hai đ ng th ng ạ ộ ỉ ủ ạ ầ ượ ằ ườ ẳ
1
∆
,
2
∆
,
c nh còn l i nh n I làm trung đi m.ạ ạ ậ ể
c) Tìm to đ đi m M thu c đ ng th ng ạ ộ ể ộ ườ ẳ
2
∆
sao cho t M có th k đ c hai ti p tuy nừ ể ẻ ượ ế ế
vuông góc t i đ ng tròn ớ ườ
( ) ( ) ( )
2 2
: 1 4 4C x y+ + − =
II . PH N RIÊNG ( 3 đi m ) Ầ ể
Thí sinh ch đ c làm m t trong hai ph n (ph n 1 ho c ph n 2)ỉ ượ ộ ầ ầ ặ ầ
1. Dành cho h c sinh h c theo ch ng trình chu nọ ọ ươ ẩ
a) Gi i b t ph ng trình: ả ấ ươ
2
4 3 2 5x x x− + − < −
b) Ch ng minh đ ng th c sau ( gi thi t bi u th c luôn có nghĩa)ư ẳ ư ả ế ể ư
1 cos2 1 cos4
. cot
cos2 sin4
x x x
x x
+ + =
c) Vi t ph ng trình chính t c c a elip bi t tr c nh b ng 4, tiêu c ế ươ ắ ủ ế ụ ỏ ằ ự
2 5
.
2. Dành cho h c sinh h c theo ch ng trình nâng caoọ ọ ươ
a) Gi i b t ph ng trình: ả ấ ươ
2 3 5 2x x x+ − − > −
b) Ch ng minh r ng: ư ằ
( ) ( )
2 0 0
3
cos sin 30 cos 60 4
x x x− + + =
c) Vi t ph ng trình chính t c c a hypebol bi t tr c th c b ng 6, tiêu c ế ươ ắ ủ ế ụ ự ằ ự
2 13
2
Đ 3Ề
I . PH N CHUNG CHO T T C THÍ SINH (7 đi m ) Ầ Ấ Ả ể
Câu 1. (2 đi m) Gi i các b t ph ng trình : a) ể ả ấ ươ ≥ +1 b)
Câu 2. (2 đi m) a) Gi i ph ng trình 2x + = 33 - 3xể ả ươ
b)Tính giá tr bi u th c ị ể ư
0 0
0 0 0 0
cos 20 cos80
sin 40 .cos10 sin10 .cos 40
A−
=+
Câu 3. (3 đi m) Trong m t ph ng to đ Oxy, cho đi m A(3;-1),B(-4;0),C(4;0) và đ ng th ngể ặ ẳ ạ ộ ể ườ ẳ
d có ph ng trình 2x-3y+1=0ươ
a)Vi t ph ng trình đ ng th ng qua A và ế ươ ườ ẳ ⊥ d
b)Vi t ph ng trình đ ng tròn ngo i ti p ế ươ ườ ạ ế ∆ABC
c)M là m t đi m tuỳ ý sao cho chu vi c a tam giác ABC b ng 18. CMR M luôn n m trên m tộ ể ủ ằ ằ ộ
(E) c đ nh. Vi t ph ng trìn chính t c c a (E) đóố ị ế ươ ắ ủ
II . PH N RIÊNG ( 3 đi m ) Ầ ể
Thí sinh ch đ c làm m t trong hai câu (vâu 4a hoăccâu 4b)ỉ ượ ộ
Câu 4a. Dành cho h c sinh h c theo ch ng trình chu nọ ọ ươ ẩ
a). Cho bi tế
tan 3
α
=
. Tính giá tr : ị
2sin cos
sin 2 cos
A
α α
α α
+
=−
b) Gi i h ph ng trình ả ệ ươ
2 2
7
10
x y xy
x y
+ + =
+
++ =
+
c) Cho hai s d ng a ,b . Ch ng minh r ng : ố ươ ư ằ
2ab
1 1
a b
a
+
Tìm giá tr nh nh t c a hàm s ị ỏ ấ ủ ố
4 9
yx 1 x
= + −
v i 0 < x < 1 .ớ
Câu 4b. Dành cho h c sinh h c theo ch ng trình nâng caoọ ọ ươ
a) ∆ABC có các góc A,B,C tho mãn: cosA+cosB= sinA.cosB+sinB.cosA. CMR ả∆ABC vuông
b) Tìm m đ pt sau ể
2
( 2) ( 4) 2 0m x m x m
+ − + + − =
có ít nh t m t nghi m d ng ấ ộ ệ ươ
c) Tìm giá tr nh nh t c a hàm s ị ỏ ấ ủ ố
4 9
yx 1 x
= + −
v i 0 < x < 1 .ớ
Đ 3Ề
PH N CHUNG DÀNH CHO T T C H C SINH: (7,0 đi m)Ầ Ấ Ả Ọ ể
Câu I. (1,0 đi m) Gi i b t ph ng trình: ể ả ấ ươ
2
4 3 1
3 2
− + < −
−
x x x
x
Câu II:(2,0 đi m) 1)Gi i ph ng trình: ể ả ươ
2
x 3x 2 = 0−−
.
2)Tìm các giá tr c a m đ bi u th c sau luôn không âm:ị ủ ể ể ư
f(x) = m.x2 – 4x + m
3
Câu III:(2,0đ) 1) Cho 900 < x < 1800 và sinx =
3
1
. Tính giá tr bi u th cị ể ư
xx
xx
M
2
2
cottan.2
sincos.2
+
+
=
2) Cho a, b, c l n l i là đ dài 3 c nh c a tam giác ABC. CMR: ầ ượ ộ ạ ủ
222
222
Btan
Atan
acb
bca
−+
−+
=
Câu IV:(1,0 đi m) ể
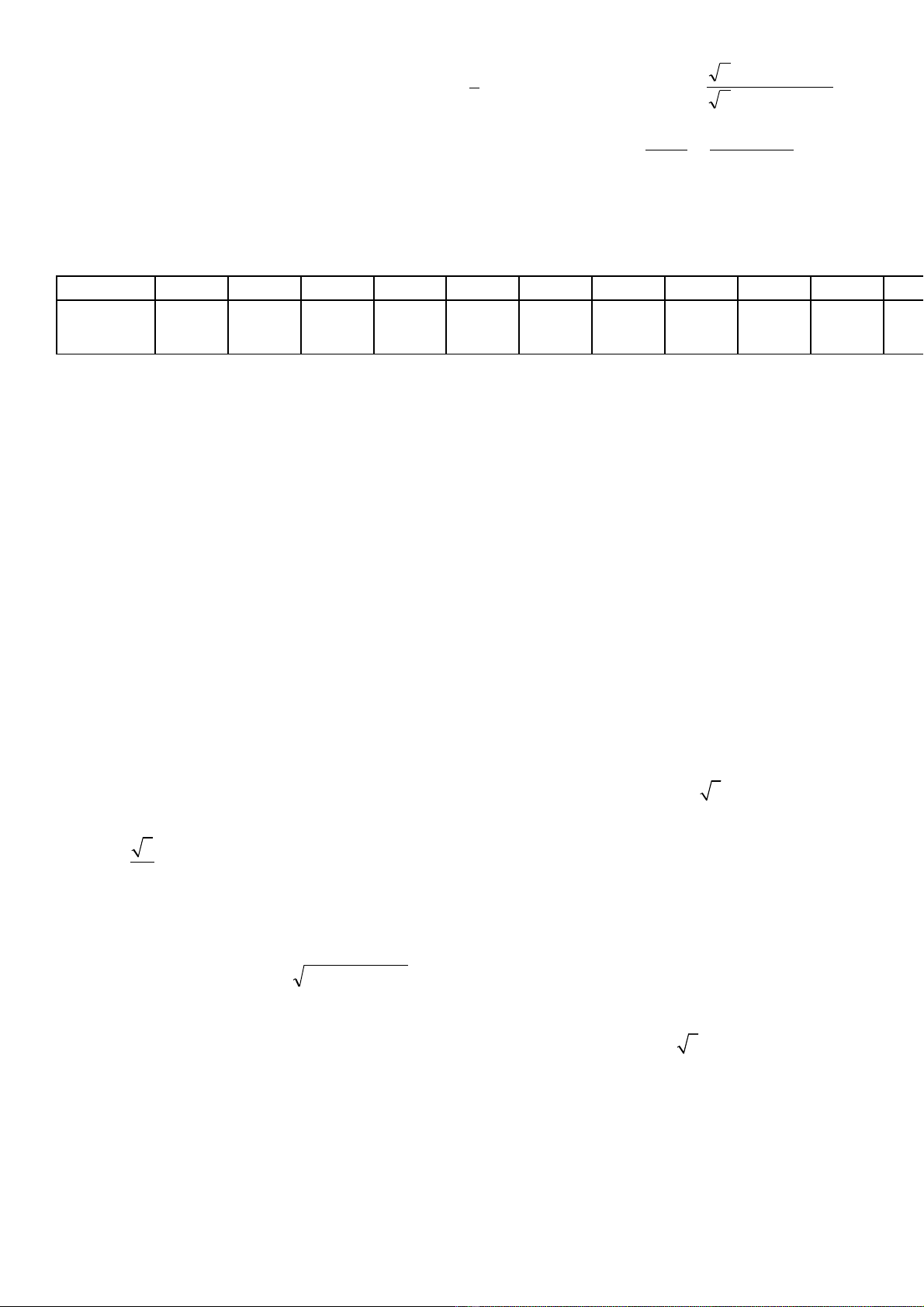
S l ng sách bán ra c a m t c a hàng các tháng trong năm 2010 đ c th ng kê trong b ng sauố ượ ủ ộ ử ượ ố ả
đây ( s l ng quy n):ố ượ ể
Tháng 1 2 3 4 5 6 7 8 9 10 1
Số
l ngượ 430 560 450 550 760 430 525 410 635 450 8
Tính s trung bình và s trung v c a m u s li u tố ố ị ủ ẫ ố ệ rên.
Câu V:(1,0 đi m) ể
Trong m t ph ng Oxy cho đi m M(9; 1). L p ph ng trình đ ng th ng (d) đi qua M c t các tiaặ ẳ ể ậ ươ ườ ẳ ắ
Ox, Oy l n l t t i A; B sao cho di n tích ầ ượ ạ ệ
OAB
∆
nh nh t.ỏ ấ
II. PH N RIÊNG: (3,0 đi m) Ch n A ho c BẦ ể ọ ặ
A.Dành cho h c sinh h c ch ng trình chu n.ọ ọ ươ ẩ
Câu VIa:(1,0 đi m)ể
Tìm các giá tr c a m đ ph ng trình (m + 2)xị ủ ể ươ 2 + 2(2m - 3)x + 5m - 6 = 0 có hai nghi m phânệ
bi t trái d u.ệ ấ
Câu VII.a:(2,0 đi m)ể
Trong m t ph ng Oxy cho đi m A(- 2; 3) và đ ng th ng (D) có ph ng trình 3x + y - 7 = 0.ặ ẳ ể ườ ẳ ươ
Vi t ph ng trình tham s c a đ ng th ng ế ươ ố ủ ườ ẳ
∆
đi qua A vuông góc v i (D) và tìm t a đ giaoớ ọ ộ
đi m M c a ể ủ
∆
v i (D).ớ
Vi t ph ng trình chính t c c a elip (E) bi t (E) có m t tiêu đi m ế ươ ắ ủ ế ộ ể
( )
F 3;0−
và đi qua đi mể
3
M 1; 2
� �
� �
� �
� �
.
B. Dành cho h c sinh h c ch ng trình nâng cao.ọ ọ ươ
Câu VI.b:(1,0 đi m)ể
Gi i ph ng trình sau: 9ả ươ
91620145 22 ++−=++− xxxx
.
Câu VIIb:(2,0 đi m) ể
Vi t ph ng trình chính t c c a Hypebol (H) bi t (H) đi qua đi m ế ươ ắ ủ ế ể
( )
2; 3
và m t đ ng ti mộ ườ ệ
c n c a (H) t o v i tr c tung m t góc 30ậ ủ ạ ớ ụ ộ 0.
Trong m t ph ng to đ Oxy cho hình ch nh t ABCD tâm I có c nh AB n m trên đ ng th ngặ ẳ ạ ộ ữ ậ ạ ằ ườ ẳ
+=
=
ty
tx
1
3
và AB = 2.AD.
L p ph ng trình đ ng th ng AD, BCậ ươ ườ ẳ
4
Đ 4Ề
PH N CHUNG DÀNH CHO T T C H C SINH: (7,0 đi m)Ầ Ấ Ả Ọ ể
Câu 1: 1)Gi i BPT : ả
1
32
1
2
1
1
32
+
+
≤
+−
+
+
x
x
xx
x
2) Cho bt f(x)=4x2 – (3m +1 )x – (m + 2)
Tìm m đ pt f(x)=0 có 2 nghi m phân bi tể ệ ệ
Tìm m đ f(x) > 0 vô nghi m. ể ệ
Câu 2: a)Tính giá tr l ng giác c a cung 75ị ượ ủ 0
b) CMR : c)tan300 + tan400 + tan500 + tan600 =
8 3
3
Cos200
c)Gi i b t ph ng trình 2xả ấ ươ 2 +
151065
2+>−− xxx
Câu 3: Cho ∆ABC có góc A = 600 bán kính đ ng tròn ngo i ti p R= , bán kính đ ng trònườ ạ ế ườ
n i ti p r = . Tim chu vi vaø dieän tích ộ ế ∆ABC .
II. PH N RIÊNG: Ch n A ho c BẦ ọ ặ
Câu A Cho đ ng th ng ( d): x – 2y –2 = 0 và A(0;6) ; B(2 ;5) ườ ẳ
Vi t pt tham s c a ABế ố ủ
Xét v trí t ng đ i c a AB và (d) .Tính kho ng cách t A đ n (d)ị ươ ố ủ ả ừ ế
Vi t pt các c nh c a ế ạ ủ
ABC∆
cân t i C, bi t ạ ế C thu c (d) ộ
Câu B:ho đ ng tròn (C) : xườ 2 + y2 + 2x – 4y = 0
Xác đ nh tâm và bán kính(C)ị
Vi t pt đt d bi t d qua A(1;2) và c t (C) t i hai đi m phân bi t P,Q sao cho A là TĐ c a PQế ế ắ ạ ể ệ ủ
Vi t pt tt c a (C) bi t tt qua M( -2 ;4) ế ủ ế
Đ 5Ề
CÂU 1 Gi i b t ph ng trình sau ả ấ ươ
1
56
311
2
2
−≥
+−
−+
xx
xx
CÂU 2 Gi i ph ng trình sau ả ươ
xxxx 88)18(3
22
+=−+
CÂU 3 Ch ng minh r ng v i m i x ta có ư ằ ớ ọ
1)(cos2
2
coscos
244
−+=
−− xxx
π
π
CÂU 4 Cho elip (E):
1
916
22
=+ yx
Tìm tâm sai và tiêu c c a ự ủ (E).
Vi t ph ng trình đ ng tròn ngo i ti p hình ch nh t c s c aế ươ ườ ạ ế ữ ậ ơ ở ủ (E)
Tìm đi m ểM thu c (E) sao cho ộ
12 2M FM F =
(F1 và F2 là hai tiêu đi m c a (E) ể ủ
CÂU 5 Tìm GTNN c a hàm sủ ố
22
2
11
2
1
)(
++
+=
x
xxf
v i ớ
2≥x
5