TR NG CĐCNTT TP.HCMƯỜ Đ THI MÔN TÓAN R I R C & LÝ THUY T Đ THỀ Ờ Ạ Ế Ồ Ị
Khoa CNTT L P: LT2011-L n 1-Đ 1.Ớ ầ ề
* * * (TG 90 phút – đ c xem tài li u)ượ ệ
Bài 1:
Ch ng minh bi u th c m nh đ sau là h ng đúngứ ể ứ ệ ề ằ
((a ∨ b) → (b∨ c)) ∨ ((a ∨ b) ∧ ┐(b∨ c))
Bài 2:
M t m t kh u ph i có đ dài 6 ký t (không phân bi t ký t hoa, th ng), m i ký t đ cộ ậ ẩ ả ộ ự ệ ự ườ ỗ ự ượ
l y t b ng 26 ch cái và 10 ch s . Tính s m t kh u có th t o ra trong m i tr ng h pấ ừ ả ữ ữ ố ố ậ ẩ ể ạ ỗ ườ ợ
sau:
a) Không có đi u ki n gì thêm.ề ệ
b) Trong m t kh u ph i có ít nh t m t ký t s .ậ ẩ ả ấ ộ ự ố
c) Trong m t kh u ph i có ít nh t m t ký t ch và có ít nh t m t ký t s .ậ ẩ ả ấ ộ ự ữ ấ ộ ự ố
Bài 3:
Tìm các công th c đa th c t i ti u c a hàm Bool sau, b ng ph ng pháp bi u đứ ứ ố ể ủ ằ ươ ể ồ
Karnaugh.
F(x,y,z,t) = xyzt + xy
t
+ xy
z
+
x
y
z
t
+
x
y
t
+ x
y
t
Bài 4:
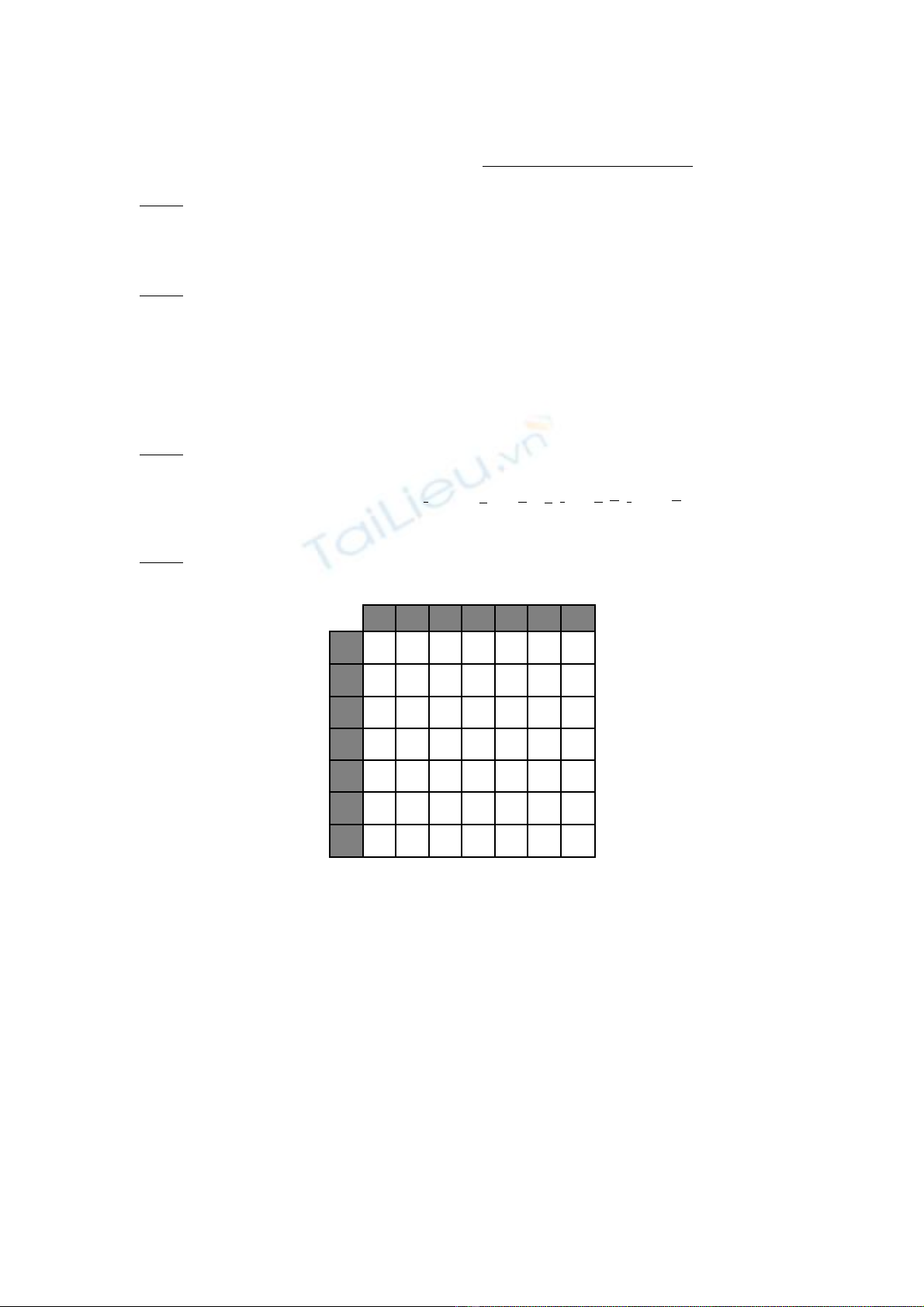
Cho đ n đ th G=(V,E) có ma tr n tr ng s nh sau (d u - là gi a 2 đ nh không có c nh):ơ ồ ị ậ ọ ố ư ấ ữ ỉ ạ
1 2 3 4 5 6 7
1 0 4 - 5
15
-
-
2 4 0
28
-
-
- -
3 -
28
0
17 30
-
12
4 5 -
17
0 -
10
7
5
15
-
30
- 0 5
15
6 - - -
10
5 0 3
7 - -
12
7
15
3 0
a) V đ th G.ẽ ồ ị
b) Th hi n s ho t đ ng c a thu t toán Dijkstra v i đ th trên, đ tìm đ ng đi ng nể ệ ự ạ ộ ủ ậ ớ ồ ị ể ườ ắ
nh t t đ nh ấ ừ ỉ 1 đ n các đ nh còn l i. Li t kê các l trình này.ế ỉ ạ ệ ộ
H t.ế
TR NG CĐCNTTƯỜ TP.HCM Đ THI MÔN TÓAN R I R C & LÝ THUY T Đ THỀ Ờ Ạ Ế Ồ Ị
Khoa CNTT L P: LT2011-L n 1-Đ 2.Ớ ầ ề
* * * (TG 90 phút – đ c xem tài li u)ượ ệ
Bài 1:
Ch ng minh bi u th c m nh đ sau là h ng saiứ ể ứ ệ ề ằ
((a ∨ b) → (b∨ c)) ∧ ((a ∨ b) ∧ ┐(b∨ c))
Bài 2:
M t m t kh u ph i có đ dài 6 ký t (không phân bi t ký t hoa, th ng), m i ký t đ cộ ậ ẩ ả ộ ự ệ ự ườ ỗ ự ượ
l y t b ng 26 ch cái và 10 ch s . Tính s m t kh u có th t o ra trong m i tr ng h pấ ừ ả ữ ữ ố ố ậ ẩ ể ạ ỗ ườ ợ
sau:
a) Không có đi u ki n gì thêm.ề ệ
b) Trong m t kh u ph i có ít nh t m t ký t A.ậ ẩ ả ấ ộ ự
c) Trong m t kh u ph i có ít nh t m t ký t A và có ít nh t m t ký t B.ậ ẩ ả ấ ộ ự ấ ộ ự
Bài 3:
Tìm các công th c đa th c t i ti u c a hàm Bool sau, b ng ph ng pháp bi u đứ ứ ố ể ủ ằ ươ ể ồ
Karnaugh.
F(x,y,z,t) = xy
z
+
x
y
z
t
+
x
y
t
+ x
y
t + xyzt + xy
t
Bài 4:
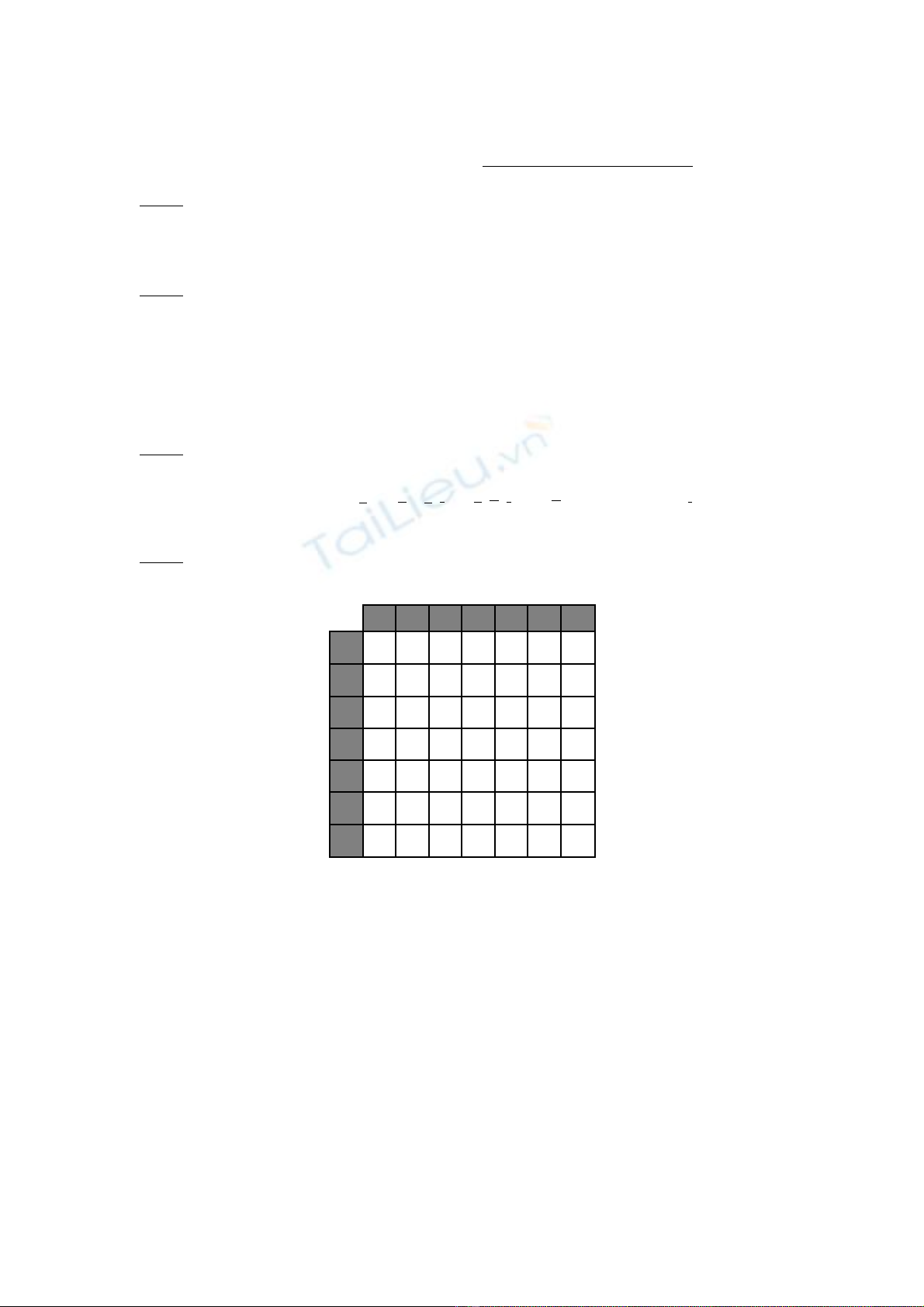
Cho đ n đ th G=(V,E) có ma tr n tr ng s nh sau (d u - là gi a 2 đ nh không có c nh):ơ ồ ị ậ ọ ố ư ấ ữ ỉ ạ
1 2 3 4 5 6 7
1 0 4 - 5
15
-
-
2 4 0
28
-
-
- -
3 -
28
0
17 30
-
12
4 5 -
17
0 -
10
7
5
15
-
30
- 0 5
15
6 - - -
10
5 0 3
7 - -
12
7
15
3 0
a) V đ th G.ẽ ồ ị
b) Th hi n s ho t đ ng c a thu t toán Dijkstra v i đ th trên, đ tìm đ ng đi ng nể ệ ự ạ ộ ủ ậ ớ ồ ị ể ườ ắ
nh t t đ nh ấ ừ ỉ 2 đ n các đ nh còn l i. Li t kê các l trình này.ế ỉ ạ ệ ộ
H t.ế









![Đề thi Toán rời rạc và Lý thuyết đồ thị cuối học kì 2 năm 2022-2023 có đáp án [kèm đề thi]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250403/laphongtrang0906/135x160/5651743650728.jpg)
















