
1
BỘ GIÁO DỤC VÀ ðÀO TẠO OLYMPIC VẬT LÝ SINH VIÊN TOÀN QUỐC – VINH 2009
HỘI VẬT LÝ VIỆT NAM
ðÁP ÁN PHẦN BÀI TẬP
CÂU 1. ðối với một mol khí thực tuân theo phương trình Van der Waals
RTbV
V
a
p=−
+)(
2
,
hãy thiết lập:
a. Phương trình ñường cong ñoạn nhiệt theo các thông số trạng thái T và V.
b. Hiệu nhiệt dung mol
Vp
CC −
như một hàm số của T và V.
Biết nội năng của một mol khí Van der Waals ñược cho bởi công thức
V
a
TCU
V
−=
.
ðÁP ÁN
a. Theo nguyên lý I,
pdV
dQ
dU
−
=
. (1)
Ta lại có
dV
V
a
dTCdV
V
U
dT
T
U
dU
V
TV
2
+=
∂
∂
+
∂
∂
= .
ðối với quá trình ñoạn nhiệt dQ = 0. Thay tất cả vào (1) ta ñược
pdVdV
V
a
dTC
V
−=+
2
.
Từ phương trình Van der Waals suy ra
2
V
a
b
V
RT
p−
−
=
. Thay vào phương
trình trên và sau khi rút gọn ta ñược
b
V
RTdV
dTC
V
−
−=
hay
)(
bVC
RdV
T
dT
V
−
−=
.
Lấy tích phân hai vế, ta ñược

2
constbV
C
R
T
V
+−−=
)ln(ln
hay
const
CR
bVT
V
=−
/
)( .
ðây chính là phương trình cần tìm.
b. Thay
dV
V
a
dTCdU
V2
+=
và
dV
V
a
bV
RT
pdV
−
−
=
2
vào (1), ta ñược
dV
b
V
RT
dTCdQ
V
−
+=
.
Với
p
không ñổi,
dTCdQ
p
=
. Thay vào phương trình trên, ta ñược
p
Vp
T
V
bV
RT
CC
∂
∂
−
+= .
Nhưng
2
V
a
b
V
RT
p−
−
=
. Lấy vi phân hai vế ta ñược (vì p = const nên vi
phân của nó bằng 0)
bV
R
T
V
V
a
bV
RT
p
−
+
∂
∂
+
−
−=
32
2
)(
0 .
Suy ra
3
2
32
)(2
1
2
)(
)/(
RTV
bVa
bV
V
a
bV
RT
bVRT
T
V
T
p
−
−
−
=
−
−
−
=
∂
∂ .
Cuối cùng ta có
3
2
)(2
1
RTV
bVa
R
CC
Vp
−
−
=− .
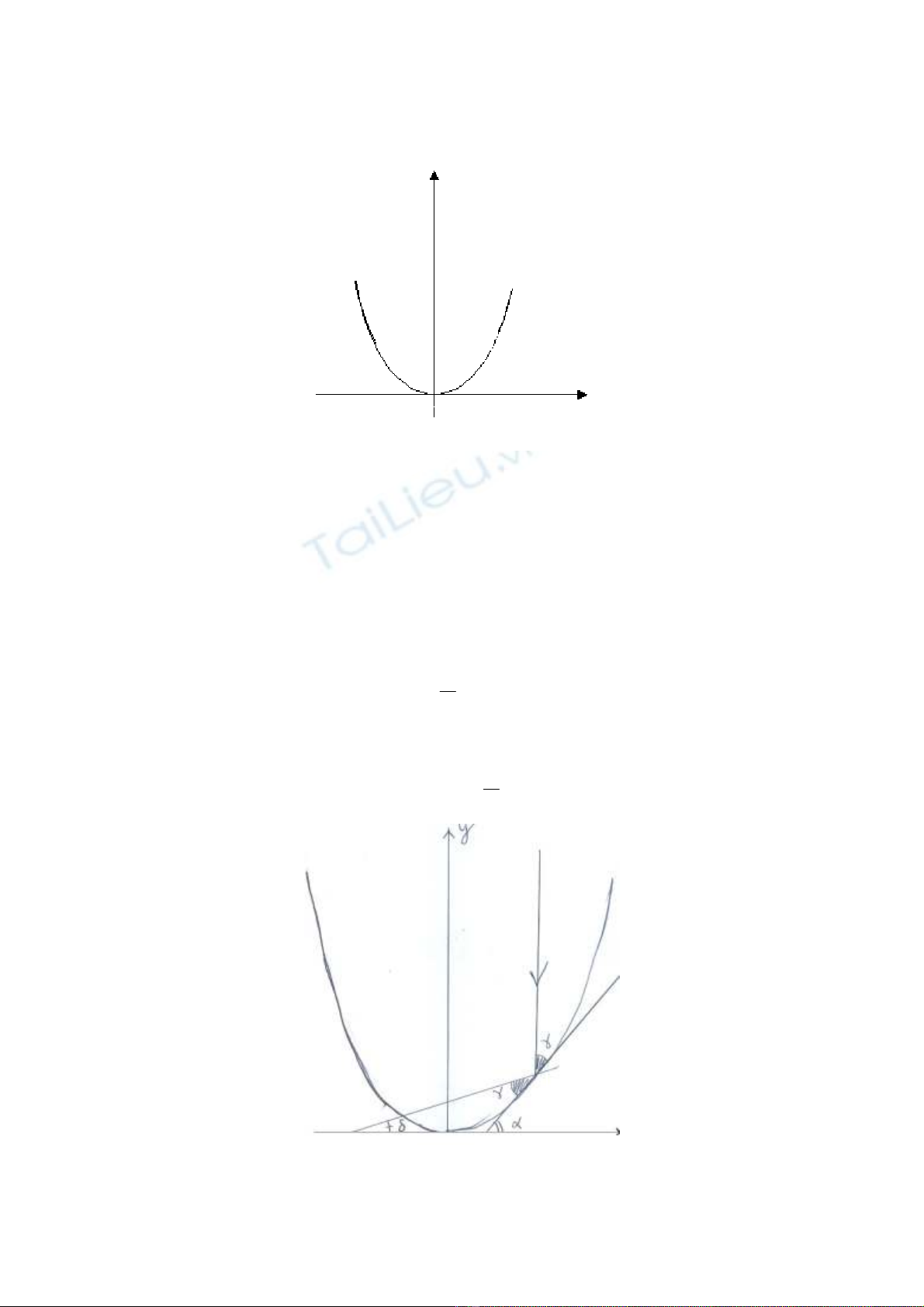
CÂU 2. Một gương parabol (xem hình vẽ) tạo ra bằng cách cho parabol
2
xy
β
=
quay xung quanh trục Oy của nó (
β
là hằng số cho trước). Người ta
chiếu tới gương hai tia sáng song song với trục Oy. Biết rằng hai tia lần lượt
cách trục này một khoảng là
l
và
l
2
. Hỏi sau khi phản xạ, tia nào cắt trục Oy
3
ở gần gốc O hơn? Tìm khoảng cách từ giao ñiểm của tia ñó với trục Oy ñến
gốc tọa ñộ.
ðÁP ÁN
Xét tia cách trục Oy một khoảng
l
. ðiểm tới M của tia này có tọa ñộ là
(
2
;ll
β
). Tiếp tuyến với gương tại M có hệ số góc
l
M
y
β
α
2
)
(
'
tan
=
=
.
Dễ thấy góc lập bởi tia tới với tiếp tuyến tại M là
α
π
γ
−=
2
.
Góc lập bởi tia phản xạ và trục Ox là
2
2
π
αδ
−=
.
Hệ số góc của tia phản xạ là
y
x
O
y=
β
x
2
M

4
α
α
α
αδ
tan
2
tan1
2
tan
1
2cottan
2
−
−=−=−= .
Phương trình của tia phản xạ là
α
αβ
tan
2
tan1
22
−
−=
−
−
l
x
ly .
Giao ñiểm của tia phản xạ với trục Oy có tọa ñộ );0(
0
y. Thay vào phương
trình trên, ta ñược
α
α
β
tan
2
tan1
2
2
0
−
−=
−
−
l
ly
hay
(
)
l
ll
l
l
ly
β
β
β
α
α
β
4
41
tan2
)tan1(
22
2
2
2
0
−
+=
−
+=
ββ
ββ
4
1
4
414
2222
=
−+
=ll .
Vì
0
y là hằng số không phụ thuộc
l
, nên tất cả các tia phản xạ ñều hội tu về
ñiểm trên trục Oy có tọa ñộ )
4
1
;0(
β
hay nói cách khác, tất cả các tia tới sau
khi phản xạ trên gương ñều cắt trục Oy tại ñiểm cách gốc tọa ñộ cùng một
khoảng bằng
β
4
1.
CÂU 3. Một hạt tương ñối tính có khối lượng nghỉ m
1
bay ñến va chạm với
hạt có khối lượng nghỉ m
2
ñứng yên (hạt bia) trong phòng thí nghiệm.
a. Nếu hạt mới có khối lượng nghỉ M ñược tạo thành do va chạm dẫn tới
sự huỷ hạt tới và hạt bia thì ñộng năng của hạt tới là bao nhiêu? Hãy xác
ñịnh giá trị khả dĩ của M.
b. Tốc ñộ của hạt mới tạo thành là bao nhiêu nếu xét trong hệ quy chiếu
phòng thí nghiệm?
c. Giả sử hạt mới (trong mục a.) phân rã thành hai hạt ñồng nhất. Quan sát
trong phòng thí nghiệm thì mỗi hạt có năng lượng E và góc θ ñối với
hướng bay của hạt tới. Hỏi khối lượng nghỉ của mỗi hạt này là bao
nhiêu?
ðÁP ÁN
a. Ký hiệu p
1
và P lần lượt là xung lượng của hạt khối lượng m
1
và hạt khối
lượng M. Xét trong hệ quy chiếu phòng thí nghiệm, theo ñịnh luật bảo toàn
năng lượng và xung lượng, ta có

5
, )Pc()(Mc cm )cp()cm(
2222
2
2
1
22
1
+=++ (1)
P p
1
=
. (2)
Từ (1) và (2) rút ra
( )
2
1
2
2
2
2
1
2
2
2
2
1mmmM
m4
1
c
p−−−=
. (3)
Vì (p1/c)2 là ñại lượng không âm nên
(
)
0m4mmmM
2
2
2
1
2
2
2
2
1
2
≥−−−
hay
0)m(m)m(m2MM
22
2
2
1
2
2
2
1
24
≥
−
+
+
−
.
Do ñó,
21
mmM
−
≤
hoặc
21
mmM
+
≥
. (4)
Mặt khác, từ (1) và (2) suy ra
22
2
2
1
22
1
2
1
22
)c(mc)(p)c(mc)(p)(Mc ++≥+
hay
2
2
2
1
2
mmM +≥ . (5)
Kết hợp (4) và (5) ta có
21
mmM
+
≥
. (6)
ðộng năng K của hạt m
1
là
2
1
2
1
22
1
2
1
cm)cp()cm(cmEK −+=−=
=
2
2
2
21
2
c
2m
)m(mM +− . (7)
b. Tốc ñộ V của hạt M ñược xác ñịnh bởi biểu thức
1
2pPV
c
V
1
M==
−
. (8)
Từ ñó rút ra
2
2
2
1
2
22
2
2
1
2
2
2
1
22
2
1
2
1
mmM
)m(m)]m2(m[MM
c
c
p
M
p
V+−
−++−
=
+
= . (9)
c.
Ký hiệu m, p và E là khối lượng nghỉ, xung lượng và năng lượng của hạt
ñược tạo thành do hạt M phân rã ra. Ta có
















