WWW.VNMATH.COM
Đ s 14ề ố
Đ ÔN T P H C KÌ 2 – Năm h c Ề Ậ Ọ ọ
Môn TOÁN L p 11ớ
Th i gian làm bài 90 phútờ
Bài 1: Tính các gi i h n sau:ớ ạ
a)
( )
x
x x x
2
lim 3 2
→−∞ − + −
b)
( )
x
x x x
2
lim 4 1 2
→+∞ + + −
Bài 2: Ch ng minh r ng ph ng trình ứ ằ ươ
x x
3
2 10 7 0− − =
có ít nh t hai nghi m.ấ ệ
Bài 3: Tìm m đ hàm s sau liên t c t i ể ố ụ ạ x = –1
x khi x
f x x
mx khi x
2
11
( ) 1
2 1
−
< −
=+
+ ≥ −
Bài 4: Tính đ o hàm c a các hàm s sau:ạ ủ ố
a)
x
y
x
3 2
2 5
−
=+
b)
y x x x
2
( 3 1).sin= − +
Bài 5: Vi t ph ng trình ti p tuy n c a đ th hàm s ế ươ ế ế ủ ồ ị ố
yx
1
=
:
a) T i đi m có tung đ b ng ạ ể ộ ằ
.
b) Bi t ti p tuy n song song v i đ ng th ng ế ế ế ớ ườ ẳ
y x4 3= − +
.
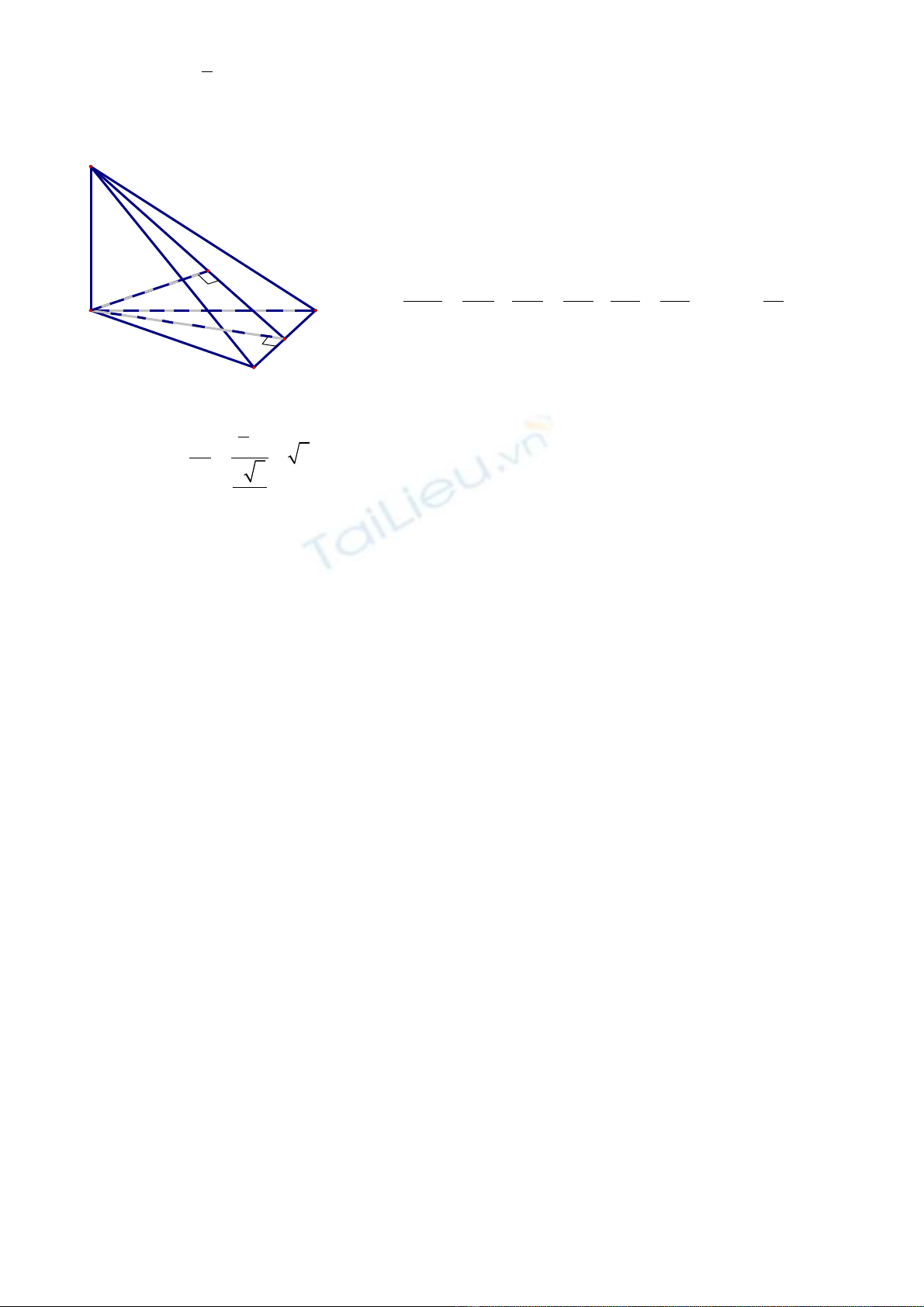
Bài 6: Cho t di n S.ABC có ứ ệ ∆ABC đ u c nh ề ạ a,
SA ABC SA a
3
( ), 2
⊥ =
. G i I là trung đi m BC. ọ ể
a) Ch ng minh: (SBC) vuông góc (SAI).ứ
b) Tính kho ng cách t A đ n (SBC).ả ừ ế
c) Tính góc gi a (SBC) và (ABC).ữ
--------------------H t-------------------ế
H và tên thí sinhọ: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . SBD :. . . . . . . . . .
1
WWW.VNMATH.COM
Đ s 14ề ố
ĐÁP ÁN Đ ÔN T P H C KÌ 2 – Năm h c Ề Ậ Ọ ọ
Môn TOÁN L p 11ớ
Th i gian làm bài 90 phútờ
Bài 1:
a)
( )
x x x x
x x x = x x x x
x x
x x
2
2 2
1 3 1 3
lim 3 2 lim . 1 2 lim . 1 2
→−∞ →−∞ →−∞
− + − − + − = − + − + −
÷ ÷
÷ ÷
=
x
xxx2
1 3
lim ( ) 1 2
→−∞
− − + + = +∞
÷
÷
b)
( )
x x x
xx
x x x
x x x
xx
2
2
2
1
1
1 1
lim 4 1 2 lim lim 4
1 1
4 1 2 4 2
→+∞ →+∞ →+∞
+
+
+ + − = = =
+ + + + + +
Bài 2: Xét hàm s ố
f x x x
3
( ) 2 10 7= − −
⇒ f(x) liên t c trên R.ụ
•
f f f f( 1) 1, (0) 7 ( 1). (0) 0− = = − ⇒ − <
⇒ PT
f x( ) 0=
có ít nh t m t nghi m ấ ộ ệ
c1( 1;0)∈ −
.
•
f f f f(0) 7, (3) 17 (0). (3) 0= − = ⇒ <
⇒ PT
f x( ) 0=
có ít nh t m t nghi m ấ ộ ệ
c2(0;3)∈
.
•
c c
1 2
≠
nên ph ng trình đã cho có ít nh t hai nghi m th c.ươ ấ ệ ự
Bài 3:
x khi x
f x x
mx khi x
2
11
( ) 1
2 1
−
< −
=+
+ ≥ −
Ta có: •
f m( 1) 2− = − +
•
x x x
x
f x x
x
2
1 1 1
1
lim ( ) lim lim ( 1) 2
1
− − −
→− →− →−
−
= = − = −
+
•
x x
f x mx m
1 1
lim ( ) lim ( 2) 2
+ +
→− →−
= + = − +
Hàm s ố
f x( )
liên t c t i ụ ạ x = –1 ⇔
m m2 2 4
− + = − ⇔ =
Bài 4:
a)
x
y
x
3 2
2 5
−
=+
⇒
xx x
x
y'= xx x x x
2
3 2 5 3(2 5) 2 6 13
2 5
2 5 (2 5) 2 5 (2 5) 2 5
+ − + − +
+= =
++ + + +
b)
y x x x y x x x x x
2 2
( 3 1).sin ' (2 3)sin ( 3 1)cos= − + ⇒ = − + − +
Bài 5:
yx
1
=
⇒
y x
x2
1( 0)
′= − ≠
a) V i ớ
y01
2
=
ta có
x
x0
0
1 1 2
2
= ⇔ =
;
y1
(2) 4
′= −
⇒ PTTT:
y x
11
4
= − +
b) Vì ti p tuy n song song v i đ ng th ng ế ế ớ ườ ẳ
y x4 3= − +
nên ti p tuy n có h s góc ế ế ệ ố k = –4
G i ọ
x y
0 0
( ; )
là to đ c a ti p ạ ộ ủ ế ⇒
x
y x
xx
0
02
00
1
12
( ) 4 4 1
2
=
′= − ⇔ − = − ⇔
= −
• V i ớ
x y PTTT y x
0 0
12 : 4 4
2
= ⇒ = ⇒ = − +
2
• V i ớ
x y PTTT y x
0 0
12 : 4 4
2
= − ⇒ = − ⇒ = − −
Bài 6:
a) Ch ng minh: (SBC) vuông góc (SAI).ứ
• SA ⊥ (ABC) ⇒ SA ⊥ BC, AI ⊥BC ⇒ BC ⊥ (SAI)
⇒ (SBC) ⊥ (SAI)
b) Tính kho ng cách t A đ n (SBC).ả ừ ế
• V AH ẽ⊥ SI (1) . BC ⊥ (SAI) ⇒ BC ⊥ AH (2)
T (1) và (2) ừ⇒AH ⊥ (SBC) nên d( A,(SBC)) = AH
•
a
AH
AH AI SA a a a
2 2 2 2 2 2
1 1 1 4 4 16 3
4
9 3 9
= + = + = ⇒ =
c) Tính góc gi a (SBC) và (ABC).ữ
•
SBC ABC BC AI BC( ) ( ) ,∩ = ⊥
, SI ⊥ BC
⇒
( )
·
SBC ABC SIA( ),( )
=
•
a
SA
SIA SIA
IA a
0
3
2
tan 3 60
3
2
= = = ⇒ =
==============================
3
I
A
B
C
S
H