2.4.3 Hàm c a các ĐLNNủ:
* Tr ng h p 1 chi uườ ợ ề :
+ X nh n các giá tr nh n ậ ị ậ
các giá tr ị
+ Xác su tấ
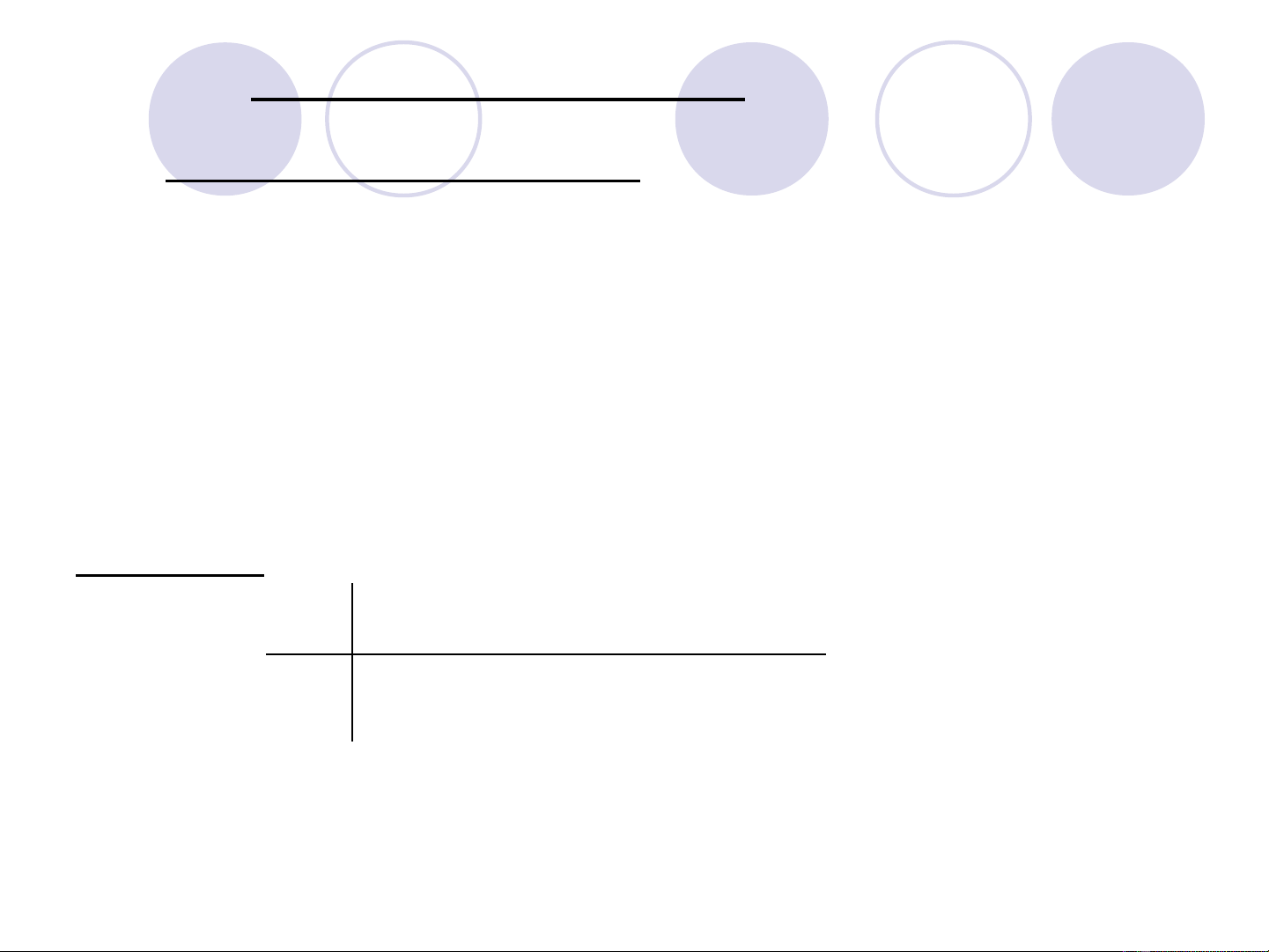
VD 2.18: Cho X có lu t phân ph iậ ố
Tìm lu t pp c a ậ ủ
Y (X)= ϕ
1 2
x ,x ,... Y
1 2
y ,y ,...
i j
j i
(x ) y
P[Y y ] p
ϕ =
= =
X
X
P
1 0 1 2
−
0,1 0,2 0,3 0,4
2
Y X
=
* Tr ng h p 2 chi uườ ợ ề :
+ Tìm giá tr c a Z t ng ng v i giá tr ị ủ ươ ứ ớ ị
c a X và Y.ủ
+ Xác su tấ
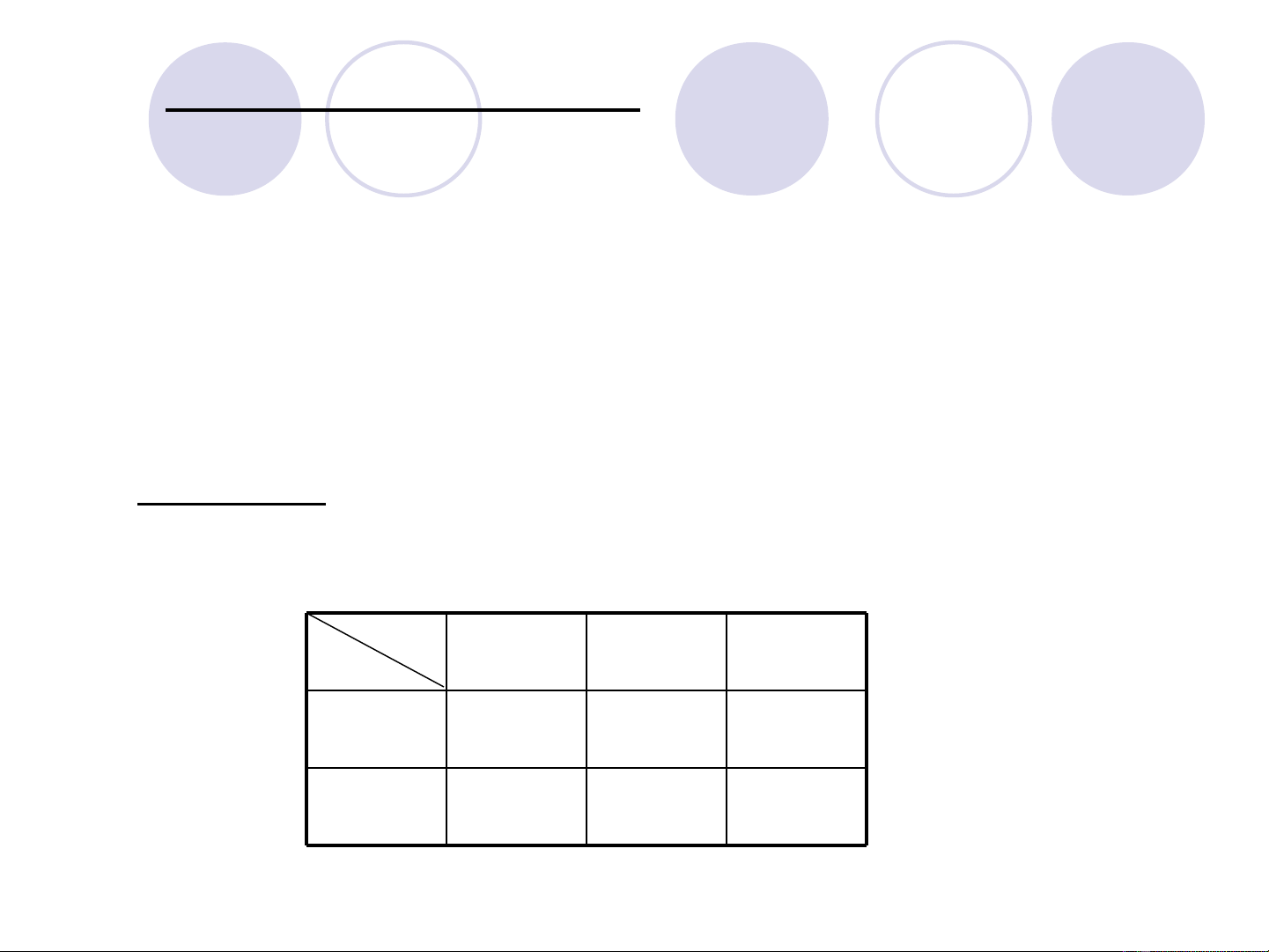
VD 2.19: Cho b ng ppxs đ ng th i c a X và ả ồ ờ ủ
Y. L p lu t pp c a ậ ậ ủ
Z (X,Y)= ϕ
i j k
k ij
(x ,y ) z
P[Z z ] p
ϕ =
= =
Z 2X Y 1= − +
0,050,250,152
0,150,30,11
210
XY
* Hàm m t đ c a m t s hàm c a ĐLNN ậ ộ ủ ộ ố ủ
hay dùng (trong th ng kê) (giáo trình trang ố
69).
2.4.4 Các s đ c tr ngố ặ ư
* M tố: Mod[X]
- V i X r i r c, Mod[X] là giá tr c a X ớ ờ ạ ị ủ
ng v i xác su t l n nh t (hay còn g i là giá ứ ớ ấ ớ ấ ọ
tr tin ch c nh t).ị ắ ấ
- V i X liên t c, Mod[X] là giá tr làm cho ớ ụ ị
hàm m t đ pp f(x) đ t giá tr l n nh t. ậ ộ ạ ị ớ ấ
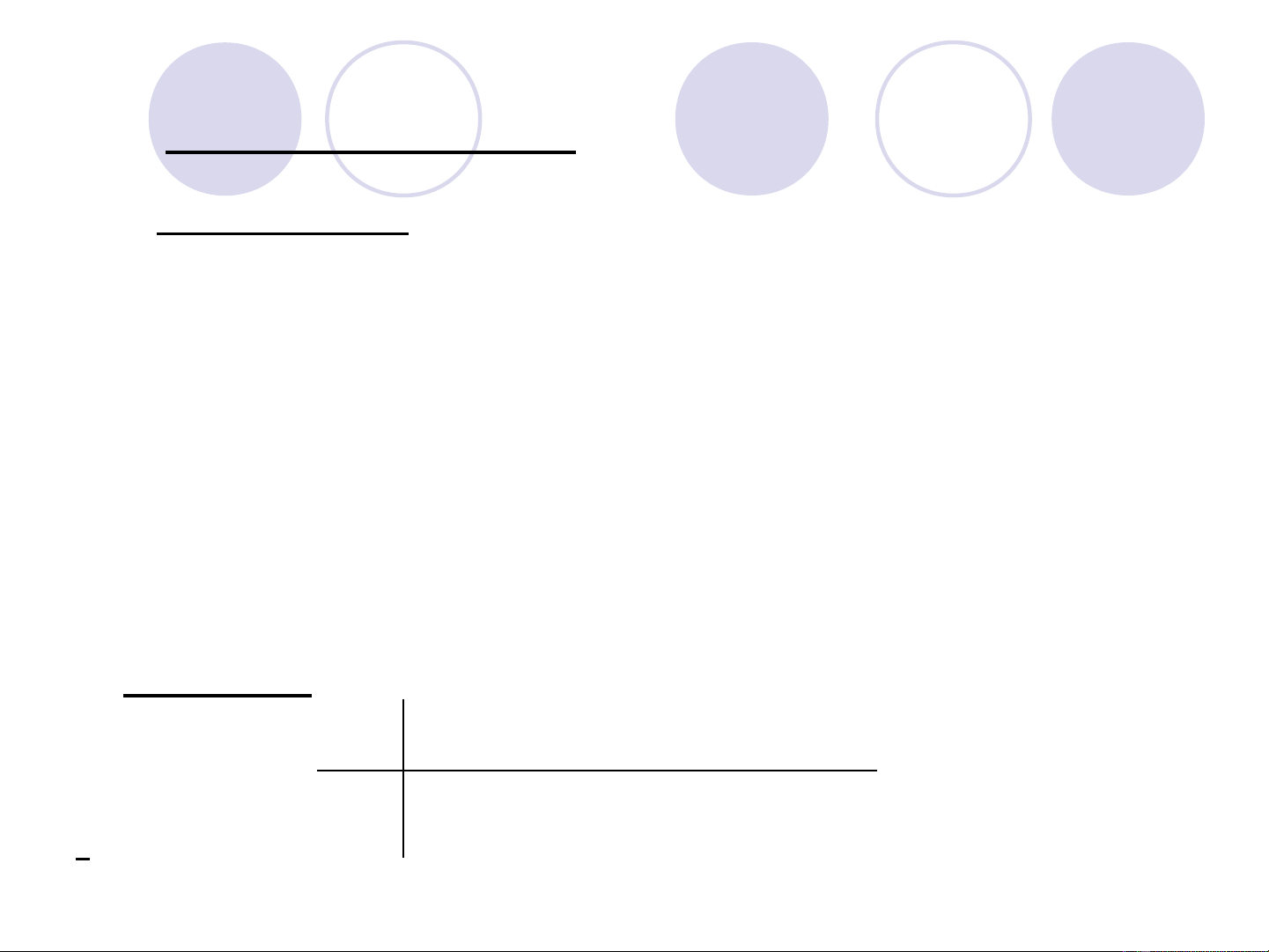
* Kỳ v ng toán h cọ ọ : M(X)
- Đ nh nghĩaị
n u X r i r cế ờ ạ
n u X liên t c có ế ụ
hàm m t đ f(x) xác ậ ộ
đ nh trên [a,b]ị
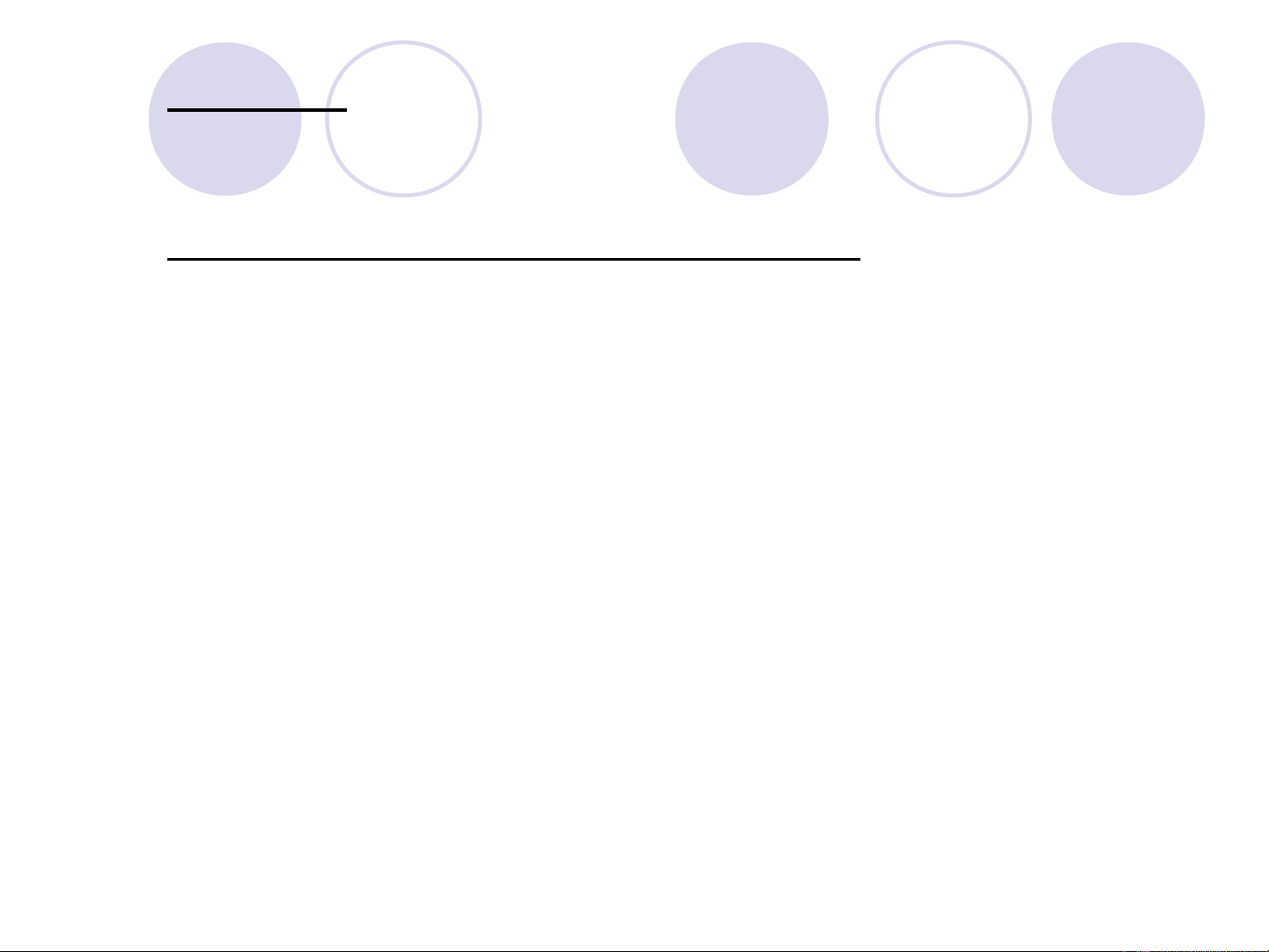
VD 2.20: Tính M(X)
n
i i
i 1
b
a
x p
M(X)
xf (x)dx
=
=
X
X
P
1 0 1 2
−
0,1 0,2 0,3 0,4
- Ý nghĩa: M(X) là giá tr trung bình (v m t ị ề ặ
xác su t) c a X. ấ ủ
- Kỳ v ng c a hàm m t ĐLNNọ ủ ộ :
Cho ĐLNN X và hàm
+ V i X r i r c:ớ ờ ạ
+ V i X liên t c có hàm m t đ pp f(x) ớ ụ ậ ộ
Y (X)= ϕ
n
i i
i 1
M(Y) M[ (X)] (x )p
=
= ϕ = ϕ
M(Y) M[ (X)] (x)f (x)dx
+
−
= ϕ = ϕ