
Giáo trình điện từ học - TS. Lưu Thế Vinh - Chương 6
lượt xem 13
download
 Download
Vui lòng tải xuống để xem tài liệu đầy đủ
Download
Vui lòng tải xuống để xem tài liệu đầy đủ
Bằng thực nghiệm người ta đã khảo sát tương tác giữa các hệ: Tương tác giữa nam châm – nam châm. Tương tác giữa nam châm – dòng điện. Tương tác giữa dòng điện – dòng điện. Các tương tác trên có cùng bản chất: tương tác giữa các điện tích chuyển động (dòng điện) gọi là tương tác từ. Tương tác từ khác với tương tác tĩnh điện
Bình luận(0) Đăng nhập để gửi bình luận!
Nội dung Text: Giáo trình điện từ học - TS. Lưu Thế Vinh - Chương 6
- - 88 - ÑIEÄN TÖØ HOÏC Chöông 6. TÖØ TRÖÔØNG TRONG CHAÂN KHOÂNG §6.1. Töông taùc töø – Ñònh lyù Ampeøre 6.1.1. Töông taùc töø. Baèng thöïc nghieäm ngöôøi ta ñaõ khaûo saùt töông taùc giöõa caùc heä: Töông taùc giöõa nam chaâm – nam chaâm. Töông taùc giöõa nam chaâm – doøng ñieän. Töông taùc giöõa doøng ñieän – doøng ñieän. Caùc töông taùc treân coù cuøng baûn chaát: töông taùc giöõa caùc ñieän tích chuyeån ñoäng (doøng ñieän) goïi laø töông taùc töø. Töông taùc töø khaùc vôùi töông taùc tónh ñieän: – Töông taùc tónh ñieän xaûy ra giöõa caùc ñieän tích ñöùng yeân vaø noù phuï thuoäc vaøo vò trí, ñoä lôùn cuûa caùc ñieän tích, xaûy ra tuaân theo ñònh luaät Coulomb. – Töông taùc töø xaûy ra giöõa caùc ñieän tích chuyeån ñoäng vaø noù phuï thuoäc vaøo tính chaát cuûa chuyeån ñoäng ñoù, xaûy ra tuaân theo ñònh luaät Ampeøre. Khi xeùt baûn chaát töø cuûa nam chaâm ta seõ thaáy tính chaát töø cuûa nam chaâm laø do caùc doøng ñieän phaân töû kheùp kín trong caùc maãu saét töø taïo ra. 6.1.2. Ñònh lyù Ampeøre. a) Phaàn töû doøng ñieän: laø moät phaàn vi phaân cuûa doøng ñieän coù chieàu daøi dl, coù r r ñoä lôùn baèng tích soá cuûa doøng ñieän I vôùi veùc tô d l : Idl . b) Töông taùc giöõa 2 phaàn töû doøng ñieän. Khaûo saùt 2 phaàn töû doøng ñieän I1 dl1 vaø I2 dl2 ñaët caùch nhau moät khoaûng r r12 (hình 6-1). n I2dl2 θ2 M r12 dF12 θ1 O I1dl1 Hình 6-1
- ÑIEÄN TÖØ HOÏC - 89 - Baèng thöïc nghieäm cho thaáy löïc taùc duïng cuûa phaàn töû doøng ñieän I1 dl1 leân phaàn töû doøng ñieän I2 dl2 coù giaù trò: 1 dF12 ⋅ I1dl1 ⋅ I 2 dl2 2 r12 sin θ1 ⋅ sin θ 2 dF12 Hay ta vieát: I1dl1 ⋅ I 2 dl2 sin θ1 sin θ 2 (6-1) dF12 = k ⋅ 2 r12 ur r Phöông cuûa d F12 ⊥ ( I 2 dl2 , n) ur r Chieàu: nhìn töø muùt cuûa d F12 thaâáy dl 2 quay cuøng chieàu kim ñoàng hoà veà r truøng vôùi n theo goùc beù nhaát. Nhö vaäy r coù theå vieát bieåu thöùc veùc tô: ta rr [I 2 dl 2 × [I1dl1 × r12 ]] ur (6-2) d F12 = k ⋅ 3 r12 Trong ñoù: k laø heä soá tyû leä coù giaù trò phuï thuoäc vaøo heä ñôn vò. Trong heä μ0 , vôùi μ0 = 4π ⋅ 10 −7 H / m – haèng soá töø. SI ta coù: k= 4π Nhö vaäy coù theå vieát laïi (5-2) nhö sau: r rr μ 0 [I 2 dl 2 × [I1dl1 × r12 ]] ur (6-3) d F12 = ⋅ 3 4π r12 Chuù yù. Khaùi nieäm phaàn töû doøng ñieän chæ coù yù nghóa thuaàn tuùy toùan hoïc, noù giuùp cho vieäc tính toaùn thuaän lôïi. Vì doøng ñieän bao giôø cuõng kheùp kín, neân löïc taùc duïng leân toaøn doøng ñieän seõ laø: r r ∫ (6-4) F= dF (Toaøn doøng ñieän ) §6.2. Töø tröôøng – Ñònh lyù Biot-Savart-Laplace. 6.2.1. Khaùi nieäm töø tröôøng . Ñeå giaûi thích cô cheá töông taùc töø trong lòch söû Vaät lyù hoïc ñaõ xuaát hieän 2 quan ñieåm khaùc nhau: – Thuyeát taùc duïng xa: cho raèng töông taùc töø ñöôïc truyeàn ñi moät caùch töùc thôøi giöõa caùc doøng ñieän vaø khoâng caàn thoâng qua moät moâi tröôøng vaät chaát trung gian naøo. Khi chæ coù moät doøng ñieän thì moâi tröôøng xung quanh khoâng xaûy ra moät bieán ñoåi naøo. – Thuyeát taùc duïng gaàn: cho raèng töông taùc töø phaûi thoâng qua moät moâi tröôøng vaät chaát trung gian bao quanh caùc doøng ñieän. Löïc töông taùc ñöôïc Löu Theá Vinh
- - 90 - ÑIEÄN TÖØ HOÏC truyeàn töø phaàn naøy sang phaàn khaùc cuûa moâi tröôøng vôùi vaän toác höõu haïn (vaän toác truyeàn töông taùc). Khi chæ coù moät doøng ñieän thì moâi tröôøng xung quanh ñaõ coù nhöõng bieán ñoåi. Theo quan ñieåm duy vaät bieän chöùng ta thaáy roõ thuyeát taùc duïng xa ñaõ coâng nhaän toàn taïi chuyeån ñoäng phi vaät chaát. Ñieàu naøy khoâng theå coù ñöôïc. Vaät lyù hoïc hieän ñaïi ñaõ baùc boû thuyeát taùc duïng xa vaø coâng nhaän thuyeát taùc duïng gaàn. Ñeå giaûi thích cô cheá töông taùc töø giöõa caùc doøng ñieän caàn phaûi coâng nhaän moät thöïc theå vaät lyù laøm moâi tröôøng trung gian truyeàn töông taùc giöõa chuùng. Thöïc theå vaät lyù naøy chính laø töø tröôøng. Töø tröôøng toàn taïi xung quanh caùc doøng ñieän, thoâng qua töø tröôøng maø töø löïc ñöôïc truyeàn ñi vôùi vaän toác truyeàn töông taùc höõu haïn baèng vaän toác cuûa aùnh saùng trong chaân khoâng. – Tính chaát caên baûn cuûa töø tröôøng: taùc duïng löïc töø leân moät doøng ñieän baát kyø naøo ñaët trong noù. Töø tröôøng laø daáu hieäu toång quaùt nhaát ñeå nhaän bieát doøng ñieän. Trong phaàn sau ta seõ thaáy töø tröôøng cuõng nhö ñieän tröôøng chæ laø moät bieåu hieän cuûa tröôøng ñieän töø. Ñoù laø moät daïng cuûa vaät chaát coù ñaày ñuû caùc thuoäc tính xaùc ñònh maø con ngöôøi coù theå nhaän thöùc ñöôïc: naêng löôïng, khoái löôïng vaø xung löôïng. r r 6.2.2. Caûm öùng töø B vaø cöôøng ñoä töø tröôøng H . Ñeå ñaëc tröng ñònh löôïng cho tröôøng veà maët taùc duïng löïc ngöôøi ta ñöa ra r khaùi nieäm veùc tô caûm öùng töø B . Töø bieåu thöùc cuûa ñònh luaät Ampeøre (6-3) neáu taùch rieâng veùc tô : rr r μ 0 [I1dl1 × r12 ] (6-5) dB1 = ⋅ 3 4π r12 uu r r Ta thaáy dB1 chæ phuï thuoäc vaøo I1 dl1 vaø vò trí ta xeùt r12. Noù coù theå duøng uu r uur r ñeå ñaëc tröng cho I1 dl1 veà maëc taùc duïng löïc leân I 2 dl 2 . dB1 ñöôïc goïi laø veùc tô uu r caûm öùng töø nguyeân toá do I1 dl1 gaây ra taïi toïa ñoä r12. r Caûm öùng töø nguyeân toá dB do moät phaàn töû doøng ñieän baát kyø gaây ra: rr μ0 I [dl × r ] r (6-6) dB = ⋅ r3 4π Bieåu thöùc (6-6) ñöôïc goïi laø ñònh lyù Biot-Savart-Laplace. Chieàu cuûa veùc rr r tô dB laø chieàu cuûa tích veùc tô [dl × r ] . – Ñôn vò. Trong heä SI caûm öùng töø ño baèng Tesla (T). – Nguyeân lyù choàng chaát töø tröôøng.
- ÑIEÄN TÖØ HOÏC - 91 - Cuõng gioáng nhö ñieän tröôøng, töø tröôøng tuaân theo nguyeân lyù choàng chaát. Do doøng ñieän bao giôø cuõng kheùp kín, neân caûm öùng töø do toaøn boä doøng ñieän gaây ra taïi moät ñieåm naøo ñoù seõ baèng toång caùc caûm öùng töø nguyeân toá do taát caû caùc phaàn töû doøng ñieän taïo ra: ur uur ∫ (6-7) B= dB (Toaøn doøng ñieän ) Töø tröôøng do nhieàu doøng ñieän gaây ra taïi moät ñieåm naøo ñoù: u r uuu rrr u r nu r B = B1+B 2 +B 3 + ⋅ ⋅ ⋅ +B n = ∑ B i (6-8) i =1 ur r – Veùc tô cöôøng ñoä töø tröôøng H . Ngoaøi veùc tô caûm öùng töø B ngöôøi ta coøn r duøng veùc tô cöôøng ñoä töø tröôøng H . u r uu r B – Trong chaân khoâng: (6-9) H= μ0 ur uu r Br – Trong töø moâi : (6-10) H= −J μ0 r (Trong ñoù J – veùc tô töø hoùa, seõ xeùt trong chöông 8) 6.2.3. AÙp duïng ñònh lyù Biot-Savart-Laplace. 1) Tính töø tröôøng do moät doøng ñieän troøn gaây ra taïi moät ñieåm naèm treân truïc voøng daây. uu r r Xeùt phaàn töû doøng I dl gaây ra taïi M moät töø tröôøng nguyeân toá dB : rr μ I [dl × r ] r dB = 0 ⋅ r3 4π Töø tröôøng toaøn phaàn do doøng ñieän troøn gaây ra: u r uur B = ∫ dB L u r u r r Do tính ñoái xöùng coù theå phaân tích : dB = d B n + d B t (hình 6-2, a): ur r r r B = ∫ dB = ∫ dBn + ∫ dBt L L L r r r ∫ ∫ ∫ Ta coù: dBt = 0 ; dB cosα . dBn = L L L u r Vì taát caû caùc veùc tô d B n ñeàu cuøng phöông chieàu neân coù theå vieát: Löu Theá Vinh
- - 92 - ÑIEÄN TÖØ HOÏC Idl dBt r dB ur u r Pm B R α O M dBn h a) b) Hình 6-2 μ0 I R μI ⋅ 3 ∫ dl = 0 3 ⋅ 2π R 2 ∫ dB cosα = B= 4π r L 2π r L μ μ0 Pm Hay: (6-11) B = 0 3 ⋅ IS = 2π ( R 2 + h2 )3/ 2 2π r Vôùi : u m = ISr– moâmen töø cuûa doøng ñieän troøn (hình 6-2, c) u Pr r P m = IS n – veùc tô moâmen töø song song cuøng chieàu vôùi B . μP – Neáu h = 0 : (6-12) B0 = 0 m 2π R3 μP – Neáu R
- ÑIEÄN TÖØ HOÏC - 93 - - Maät ñoä ñöôøng söùc (soá ñöôøng söùc xuyeân qua moät ñôn vò dieän tích ñaët vuoâng goùc vôùi tröôøng) cho bieát ñoä lôùn cuûa veùc tô caûm öùng töø taïi moãi ñieåm. Ví duï: Ñöôøng söùc töø tröôøng cuûa doøng ñieän thaúng (hình 6-3, a) vaø cuûa doøng ñieän troøn (hình 6-3, b). a) b) Hình 6-3 6.3.2. Töø thoâng. u r Laø thoâng löôïng cuûa veùc tô caûm öùng töø B göûi qua moät dieän tích naøo ñoù. Ta haõy xeùt moät dieän tích dS ñaët trong tröôøng. Töø thoâng göûi qua dS coù giaù trò: ur r (6-15) dφ = B ⋅ d S = B dS cosα r r Trong ñoù: d S = dS ⋅ n – veùc tô dieän tích coù ñoä lôùn baèng dS, coù höôùng r cuûa phaùp tuyeán vôùi dieän tích n Töø thoâng toaøn phaàn göûi qua moät maët höõu haïn naøo ñoù coù giaù trò: ur r φ = ∫ dφ = ∫ B dS (6-16) S S Ñôn vò: Trong heä SI töø thoâng coù ñôn vò laø r n Webe (Wb). Do ñoù ta ñònh nghóa ñôn vò cuûa Bn caûm öùng töø B laø Tesla töø coâng thöùc ñònh nghóa töø thoâng nhö sau: [Φ ] Wb [B] = =T = α [S ] m 2 r dS B Tesla laø caûm öùng töø cuûa moät töø thoâng ñeàu 1 Veâbe xuyeân vuoâng goùc qua moät maët phaúng dieän tích 1 meùt vuoâng. Hình 6-4 6.3.3. Ñònh lyù Oxtroâgratxki – Gauss. Löu Theá Vinh
- - 94 - ÑIEÄN TÖØ HOÏC Ta haõy tính töø thoâng göûi qua moät maët kín Σ baát kyø. r Quy öôùc. Veõ phaùp tuyeán döông n cuûa maët kín höôùng töø trong ra ngoaøi maët kín. Nhö vaäy choã naøo ñöôøng söùc ñi vaøo (α>900) neân töø thoâng seõ coù giaù trò aâm, coøn choã naøo ñöôøng söùc ñi ra (α 900 Σ ∫ Φ 2 = BdS cosα 2 >0 do α2
- ÑIEÄN TÖØ HOÏC - 95 - Trong ñoù V laø theå tích giôùi haïn bôûiumaët kín Σ. Keát hôïp (6-17) ta coù: r divB = 0 (6-19) Ñaáy laø daïng vi phaân cuûa ñònh lyù O-G. uu r Töông töï, neáu vieát ñònh lyù O-G cho veùc tô cöôøng ñoä töø tröôøng H ta coù: uu r r uu r ∫ HdS = 0, divH = 0 (6-20) Σ YÙ nghóa: Caùc bieåu thöùc (6-17, 6-19, 6-20) cho raèng thaáy raèng töø tröôøng laø moät tröôøng xoaùy. Ñaây laø ñieåm cho thaáy söï khaùc bieät cô baûn giöõa töø tröôøng vaø tröôøng tónh ñieän. Ñöôøng söùc ñieän tröôøng laø nhöõng ñöôøng cong hôû, chuùng baét ñaàu vaø keát thuùc treân caùc ñieän tích (hay ôû voâ cöïc). Caùc ñöôøng söùc töø tröôøng khoâng coù ñieåm baét ñaàu vaø ñieåm keát thuùc, chuùng laø nhöõng ñöôøng cong kín. Ñieàu ñoù chöùng toû raèng trong töï nhieân khoâng toàn taïi khaùi nieäm “tö ø tích” . 6.3.4. Ñònh lyù doøng toaøn phaàn (ñònh lyù veà löu soá veùc tô B) ur a) Ñònh lyù: Trong tónh ñieän ta coù löu soá cuûa veùc tô cöôøng ñoä ñieän tröôøng E ur r ur r ∫ ∫ ñöôïc ñònh nghóa laø tích phaân Edl . Vôùi moät ñöôøng cong kín thì: Edl = 0 L Töông töï trong töø tröôøng ngöôøi ta ñònh nghóa löu soá cuûa veùc tô caûm öùng u r ur r ∫ töø B theo moät ñöôøng cong naøo ñoù laø tích phaân: Bdl . Ta haõy xeùt moät ñöôøng cong phaúng, kín L bao quanh moät doøng ñieän thaúng daøi voâ haïn (hình 6-6, a). Ñöôøng cong naèm trong maëtuphaúng vuoâng goùc r vôùi doøng ñieän. Choïn chieàu döông L laø chieàu cuûa töø tröôøng B , ta coù: 2π ur r rr ∫ ∫ ∫ ∫ Bdl = Bdl cos( B, dl ) = Brdϕ = Brdϕ 0 L L L μ0 I Trong ñoù: ; B= 2π r 2π ur r μ0 I ∫ ∫ Töø ñoù: (6-21) dϕ = μ0 I Bdl = 2π 0 L Deã thaáy, neáu chieàu döông cuûa L ngöôïc laïi thì goùc α > π/2 khi ñoù giaù trò cuûa dlcosα = rdϕ < 0. Löu Theá Vinh
- - 96 - ÑIEÄN TÖØ HOÏC r a dl α r dϕ d I u r α1 B α2 Δϕ I b L u r B a) b) c Hình 6-6 u r Nhö vaäy löu soá cuûa veùc tô B coù theå coù daáu döông hoaëc aâm tuøy thuoäc vaøo chieàu cuûa doøng ñieän. I>0 neáu chieàu cuûa L vaø I thuaän chieàu theo quy taéc vaën nuùt chai vaø ngöôïc laïi. Neáu ñöôøng cong L khoâng bao quanh doøng ñieän I (hình 6-6, b) ta coù: Treân phaàn (abc) thì goùc α < π/2 neân dlcosα = rdϕ > 0. Treân phaàn (cda) thì goùc α > π/2 neân dlcosα = rdϕ < 0. μ0 I ⎡ ⎤ μI ur r ∫ ∫ ∫ ⎢ dϕ ⎥ = 0 [Δϕ − Δϕ ] = 0 Do ñoù: dϕ + Bdl = 2π ⎢ ⎥ 2π ⎣ ( abc ) ⎦ ( cda ) L Trong ñoù: Δϕ – goùc nhìn töø I tôùi L ur r Nhö vaäy, neáu L khoâng bao quanh doøng ñieän thì ∫ Bdl = 0 . L + Trong tröôøng hôïp toång quaùt, neáu L laø moät ñöôøng cong coù daïng baát kyø r (khoâng phaúng), khi ñoù ta coù theå chia d l thaønh 2 thaønh phaàn (hình 6-7): rr r dl = dl n + dl t r ur Trong ñoù thaønh phaàn dl n ⊥ doøng ñieän I neân song song vôùi B ; coøn thaønh r u r phaàn dl t song song vôùi doøng ñieän I neân ⊥ vôùi B . Nhö vaäy: ur r ur r ur r ∫ ∫ ∫ ∫ ∫ Bdl = Bdl n + Bdl t = Bdln cosα + Bdlt cos90o L L L L L ur r ∫ Keát quaû: Bdl = μ 0 I – neáu L bao quanh doøng ñieän I. L ur r ∫ Bdl = 0 – neáu L khoâng bao quanh doøng ñieän I. L
- ÑIEÄN TÖØ HOÏC - 97 - I L dlt dl r dln u r B Hình 6-7 Toång quaùt: Xeùt cho tröôøng hôïp coù nhieàu doøng ñieän xuyeân qua L ta coù theå aùp duïng nguyeân lyù choàng chaát töø tröôøng. Ñònh lyù Ampreøre veà doøng toaøn phaàn ñöôïc phaùt bieåu nhö sau: Löu soá cuûa veùc tô caûm öùng töø theo moät ñöôøng cong kín baát kyø baèng toång ñaïi soá cöôøng ñoä doøng ñieän xuyeân qua dieän tích giôùi haïn bôûi ñöôøng cong ñoù nhaân vôùi μ0. ur r Bdl = μ0 ∑ I k ∫ (6-22) k L Quy öôùc: Ik > 0 neáu thuaän chieàu L theo quy taéc vaën nuùt chai. Ik < 0 neáu ngöôïc chieàu L. theo quy taéc vaën nuùt chai. b) AÙp duïng: Ñònh lyù doøng toaøn phaàn ñöôïc söû duïng ñeå tính toaùn töø tröôøng cuûa moät doøng ñieän naøo ñoù moät caùch nhanh choùng. Ta haõy xeùt moät soá tröôøng hôïp ñieån hình sau ñaây: Ví duï 1. Tính töø tröôøng cuûa moät doøng ñieän thaúng daøi voâ haïn, coù ñöôøng kính d=2R taïi moät ñieåm beân trong vaø taïi moät ñieåm beân ngoaøi daây daãn. Do tính chaát ñoái xöùng truï neân ñöôøng söùc töø tröôøng laø nhöõng ñöôøng troøn ñoàng taâm naèu trong maët phaúng vuoâng goùc vôùi doøng ñieän I . Giaù trò cuûa veùc tô m r caûm öùng töø B taïi moïi ñieåm treân moät ñöôøng söùc töø laø nhö nhau. Ta haõy choïn ñöôøng cong laáy tích phaân L truøng vôùi moät ñöôøng söùc töø coù baùn kính r. 1– Xeùt ñieåm M ôû beân ngoaøi daây daãn (r > R) : ur r ∫ Bdl = B ∫ dl = B ⋅ 2π r =μ0 I L L μ0 I I ; H= . (6-23) B= 2π r 2π r Löu Theá Vinh
- - 98 - ÑIEÄN TÖØ HOÏC 2– Xeùt ñieåm N beân trong daây daãn (r
- ÑIEÄN TÖØ HOÏC - 99 - μ0 NI ⎫ Bmax = B1 = ⎪ 2π R1 ⎪ B1 − B2 R2 − R1 (6-26) = ⎬ μ NI B1 R2 ⎪ Bmin = B2 = 0 ⎪ 2π R2 ⎭ Ví duï 3. Tính töø tröôøng cuûa oáng daây ñieän thaúng (xoâleânoâít) (hình 6-10) . OÁng daây ñieän thaúng daøi coù theå xem nhö laø moät ñoaïn cuûa oáng daây hình xuyeán trong tröôøng hôïp giôùi haïn khi taêng baùn kính hình xuyeán leân voâ haïn : R1, R2 →∞ khi ñoù theo (6-26) ta coù: Hình 6-10 B1 − B2 = 0 ⇒ B1 = B2 B1 Töø tröôøng trong loøng oáng daây ñöôïc xem nhö ñeàu, vaø coù theå aùp duïng keát quaû (6-25) ñeå tính töø tröôøng: μ NI (6-27) B = 0 = μ0 nI 2π r N Trong ñoù: n = – soá voøng treân moät ñôn vò daøi; 2π r nI – soá ampevoøng/meùt. Trong thöïc teá, nhöõng oáng daây coù chieàu daøi lôùn hôn möôøi laàn ñöôøng kính cuûa noù coù theå xem töø tröôøng trong loøng oáng laø ñeàu vaø coù theå aùp duïng keát quaû (6-27) ñeå tính. §6.4. Taùc duïng cuûa töø tröôøng leân doøng ñieän. 6.4.1. Taùc duïng cuûa töø tröôøng leân moät phaàn töû doøng ñieän Theo ñònh lyù Ampeørr löïc taùc duïng cuûa ue töø tröôøng coù caûm öùng töø B leân moät phaàn töû doøng ñieän ñöôïc xaùur ñònh bôûi phöông trình: c r uu r d F = I [dl ⋅ B] ru r – Ñoä lôùn: dF = IdlB sin(dl,B) ; r uu r – Phöông vuoâng goùc vôùi maët phaúng (dl, B) ; – Chieàu: Xaùc ñònh theo quy taéc baøn tay traùi: Hình 6-11 “Cho ñöôøng söùc töø xuyeân qua loøng baøn tay, Löu Theá Vinh
- - 100 - ÑIEÄN TÖØ HOÏC chieàu töø coå tay tôùi ngoùn tay laø chieàu doøng ñieän thì chieàu doaõi ra cuûa ngoùn caùi chæ chieàu töø löïc ” (hình 6-11). 6.4.2. Taùc duïng giöõa hai doøng ñieän thaúng song song, daøi voâ haïn. Xeùt hai doøng ñieän thaúng song song daøi voâ haïn, ñaët caùch nhau moät khoaûng d, coù caùc doøng ñieän I1 vaø I2 chaïy qua (hình 6-12). Moãi doøng ñieän taïo ra xung quanh moät töø tröôøng vaø taùc duïng löïc töø leân doøng ñieän kia. Caûm öùng töø do doøng ñieän I1 I2 I1 gaây ra taïi ñieåm ñaët cuûa moät phaàn töû uu u rr ur baát kyø I 2 dl2 coù giaù trò: d F 12 μI B1 = 0 1 2π d uu r B1 Coù phöông vuoâng goùc vôùi maët phaúng chöùa hai doøng ñieän, coù chieàu xaùc ñònh theouuquy taéc caën nuùt chai (xem d ru r hình veõ). I 2 dl2 chòu taùc duïng töø löïc: ur ru r d F12 = I 2 [dl 2 ⋅ B1 ] Hình 6-12 Coù ñoä lôùn: μ 0 I1I 2 dl2 . (6-28) dF12 = 2π d ur ur u r Phöông cuûa d F12 vuoâng goùc vôùi B1 vaø dl2 , töùc naèm trong maët phaúng chöùa hai doøng ñieän vaø coù chieàu xaùcurñònh theo quy taéc baøn tay traùi. Neáu doøng I2 chaïy cuøng chieàu vôùi I1 thì löïc d Fur höôùng veà phía doøng I1 (bò huùt), ngöôïc 12 laïi neáu hai doøng traùi chieàu nhau thì d F12 seõ höôùng ra xa (bò ñaåy). ur r Moät caùch töông töï, löïc taùc duïng cuûa doøng I2 leân moät phaàn töû doøng ñieän I1dl1 coù giaù trò: μ I I dl (6-29) dF21 = 0 1 2 1 = dF21 2π d ur ur Veá maët phöông chieàu: d F12 = − d F 21 ur Sau khi xaùc ñònh veà maët phöông chieàu cuûa d F12 theo nhö treân ta ñi ñeán keát luaän raèng neáu hai doøng ñieän I1 vaø I2 cuøng chieàu chuùng seõ huùt nhau, ngöôïc chieàu chuùng seõ ñaåy nhau. Töông taùc giöõa hai doøng ñieän thaúng daøi voâ haïn ñöôïc duøng ñeå ñònh nghóa ñôn vò ño cöôøng ñoä doøng ñieän: Ampe. “Ampe laø cöôøng ñoä cuûa moät doøng ñieän khoâng ñoåi theo thôøi gian, khi chaïy qua hai daây daãn thaúng, song song, daøi voâ haïn, coù tieát dieän nhoû khoâng
- ÑIEÄN TÖØ HOÏC - 101 - ñaùng keå, ñaët trong chaân khoâng caùch nhau 1 meùt, thì gaây ra treân moãi meùt daøi cuûa moãi daây daãn moät löïc baèng 2.10–7 Niutôn ”. Töø ñònh nghóa Ampe, ta coù theå xaùc ñònh haèng soá μ0 nhö sau: 1.1 2.10 −7 = μ0 ⋅ ⋅1 2π .1 μ0 = 4π.10 –7 ñôn vò SI Töø ñoù: 6.4.3. Maïch ñieän kín trong töø tröôøng ñeàu. ur Ñaët trong töø tröôøng ñeàuu B moät khung daây daãn hình chöõ nhaät (a,b) coù r doøng ñieän I chaïy qua, sao cho B ⊥ b. Giaû söû khung cöùng khoâng bò bieán daïng. (hình 6-13). Hình 6-13 u r ru r r uu r uu r Caùc caïnh a seõ chòu caùc löïc : f a = I [a ⋅ B] , vôùi a = a.dl , trong ñoù dl laø ur veùc tô höôùng doïc caïnh a theo chieàu doøng ñieän. Chieàu cuûa caùc löïc f a coù xu höôùng keùo daõn khung. Caùc caïnh b naèm vuoâng goùc vôùi töø tröôøng, neân moãi caïnh seõ chòu taùc duïng moät löïc coù ñoä lôùn: f = I bB Caùc löïc naøy vuoâng goùc vôùi b vaø höôùng ngöôïc chieàu nhau taïo thaønh moät ngaãu löïc, coù taùc duïng quay khung veà vò trí sao cho khung vuoâng goùc vôùi töø tröôøng. Ngaãu löïc M coù ñoä lôùn: M = f.a.sinα = IB ab sinα = IBS sinα M = PmB sinα . Vôùi Pm = IS – moâmen töø cuûaukhung. ur u r Ñeå yù ñeán phöông chieàu cuûa M & P m ta coù theå vieát: uu r uu rr M = ⎡Pm ⋅ B⎤ (6-30) ⎣ ⎦ Löu Theá Vinh
- - 102 - ÑIEÄN TÖØ HOÏC Moâmu ngaãu löïc M coù xu höôùng quay khung sao cho veùc tô moâmen töø en r u r cuûa khung P m veà truøng vôùi phöông cuûa töø tröôøng B . ur u r – Neáu P m ↑↑ u , α = 0 – ta coù vò trí caân baèng beàn; B ur r – Neáu P m ↑↓ B , α = π – Ta coù vò trí caân baèng khoâng beàn. Keát quaû treân ñuùng vôùi moät khung daây kín, phaúng, coù hình daïng baát kyø. Thaät vaäy, ta haõy chia nhoû khung thaønh caùc daõi hình chöõ nhaät nhoû, sao cho doøng chaïy treân caùc khung ñoù cuøng chieàu vôùi voøng daây. Caùc doøng ñieän cuûa caùc khung daây ôû phía trong seõ trieät tieâu laãn nhau töøng ñoâi moät (hình 6-14) vì chuùng chaïy ngöôïc chieàu nhau. Treân moãi “khung” hình chöõ nhaät seõ chòu taùc duïng cuûa moät moâmen ngaãu löïc: Mk = IBSk sinα Trong ñoù Sk – dieän tích cuûa khung thöù I k. Do höôùng cuûa caùc moâmen Mk laø truøng nhau neân moâmen toaøn phaàn taùc duïng leân voøng daây seõ laø: M = IBsinα ΣSk = IBS sinα Trong ñoù ΣSk = S – dieän tích toaøn phaàn Hình 6-14 cuûa voøng daây. Töø ñoù: uu r uu rr M = ⎡Pm ⋅ B⎤ ⎣ ⎦ 6.4.4. Maïch ñieän kín trong töø tröôøng khoâng ñeàu Xeùt moät voøng daây daãn kín, phaúng coù doøng I chaïy qua ñaët trong moät töø u r tröôøng khoâng ñeàu B . Moãi phaàn töû cuûa voøng daây chòu taùc duïng cuûa moät löïc ur u r d F vuoâng goùc vôùi voøng daây vaøurvôùi töø tröôøng B . Nhöng do caùc ñöôøng söùc töø u r B laø khoâng ñeàu, neân caùur löïc d F seõ laäp moät goùc khaùc 0 vôùi maët phaúng voøng c daây. Ta haõy phaân tích d F ra hai thaønh phaàn: ur ur ur d F = d Fn + d Ft ur Caùc thaønhuphaàn u F t song song vôùi maëtrphaúngrkhung coù taùc duïng keùo d r r u u daõn khung neáu ( P m ↑↑ B ) vaø neùn khung neáu ( P m ↑↓ B ). ur Caùcur nh phaàn d F n vuoâng goùc vôùi maët phaúng khung, hôïp laïi thaønh löïc thaø toång hôïu F n coù taùc duïng dòch chuyeån khung trong töø tröôøng (hình 6-15). Neár p uu ur r ur P m ↑↑ B khung bò huùt veà phía töø tröôøng maïnh. Ngöôùc laïi, neáu P m ↑↓ B khung bò ñaåy veà phía töø tröôøng yeáu.
- ÑIEÄN TÖØ HOÏC - 103 - ur ur d Ft dF ur d Fn ur Fn I u r B ur Pm Hình 6-15 Ta coù: ur ur ∫ Fn = d Fn L ∂B ∂B Veà ñoä lôùn cuûa löïc : , vôùi – gradien töø tröôøng theo Fn = Pm ∂n ∂n phöông phaùp tuyeán n. Nhö vaäy ta coù theå vieát döôùi daïng veùc tô: ur uu rr ⎡Pm ⋅ B⎤ (6-31) F = grad ⎣ ⎦ – ÖÙng duïng. Keát quaû nghieân cöùu treân giuùp ta giaûi thích ñöôïc taïi sao moät nam chaâm hay moät cuoän daây coù doøng ñieän chaïy qua huùt ñöôïc caùc maït saét. Döôùi taùc duïng cuûa töø tröôøng cuûa nam chaâm caùc maït saét bò töø hoùa, bieán thaønh caùc nam chaâm nhoû, coù moâmen töø xaùc ñònh, vaø chuùng bò huùt veà phía nam chaâm nôi coù töø tröôøng maïnh. Löïc taùc duïng cuûa töø tröôøng leân doøng ñieän ñöôïc öùng duïng nhieàu trong kyõ thuaät ño löôøng vaø trong kyõ thuaät ñieän ñeå cheá taïo maùy ñieän. §6.5. Coâng cuûa löïc töø. 6.5.1. Coâng cuûa löïc töø khi di chuyeån moät phaàn töû doøng ñieän ur ru r Doøng ñieän ñaët trong töø tröôøng seõ chòu taùc duïng cuûa löïc töø F = I ⎡ dl ⋅ B ⎤ . ⎣ ⎦ Khi doøng ñieän dòch chuyeån löïc töø seõ sinh coâng. Xeùt moät maïch ñieän kín ñaët trong töø tröôøng (hình 6-16). Maïch coù moät phaàn MN coù theå tröôït ñöôïc treân 2 caïnh kia. Ñoaïn maïch MN chòu taùc duïng cuûa töø löïc: F = I l B. Löu Theá Vinh
- - 104 - ÑIEÄN TÖØ HOÏC Phöông vaø chieàu cuûa löïc xaùc ñònh ur treân hình veõ 5-16 theo quy taéc nhö baøn tay traùi. Döôùi taùc duïng cuûa töø löïc F , giaû söû ñoaïn MN di chuyeån moät ñoaïn dx töø vò trí 1 sang vò trí 2. Coâng thöïc hieän trong di chuyeån ñoù seõ laø: dA = Fdx = I l B.dx = I B dS = I dΦ Trong ñoù dS laø phaàn dieän tích maø M dx ñoaïn daây MN queùt ñöôïc trong quaù trình di chuyeån, dΦ laø töø thoâng göûi qua phaàn 1 2 dieän tích dS. u r B ur Neáu töø tröôøng khoâng vuoâng goùc F ☼ vôùi maët phaúu g cuûa maïch ñieän, ta coù theå n r u r phaân tích B ra hai thaønr phaàn: B n h N u vuoâng goùc vôùi maïch vaø B t song song Hình 6-16 vôùi maïch: uu rru r B = B n + Bt . u c taùc duïng luoân vuoâng goùc vôùi töø tröôøng, neân löïc do thaønh phaàn song Löï r song B t gaây ra vuoâng goùc vôùi dòch chuyeån dx neân coâng cuûa noù baèng khoâng. u r Coâng cuûa löïc töø laø coâng do thaønh phaàn vuoâng goùc B n gaây ra, do vaäy: (6-32) dA = I Bn dS = I dΦ Trong ñoù Bn dS = dΦ laø töø thoâng do ñoaïn MN queùt ñöôïc khi di chuyeån. Neáu MN di chuyeån moät quaõng ñöôøng höõu haïn töø vò trí 1 sang vò trí 2 thì coâng cuûa löïc töø seõ laø: 2 2 A = ∫ dA = I ∫ d Φ = I (Φ 2 − Φ1 ) = I ΔΦ (6-33) 1 1 6.5.2. Maïch ñieän kín di chuyeån trong töø tröôøng. Xeùt moät maïch ñieän kín di chuyeån trong töø tröôøng, giaû söû töø tröôøng höôùng vuoâng goùc vôùi maët phaúng cuûa maïch (hình 6-17). Ñoaïn maïch abc chòu taùc duïng löïc F1 taïo vôùi phöông dòch chuyeån moät goùc α1 > π/2 neân coâng cuûa löïc sinh ra coù daáu aâm. Coâng naøy coù giaù trò baèng cöôøng ñoä doøng ñieän chaïy trong maïch, nhaân vôùi töø thoâng do phaàn maïch naøy queùt trong quaù trình di chuyeån, töùc laø: A1 = –I (Φ1 + Φ0) (6-34)
- ÑIEÄN TÖØ HOÏC - 105 - Ñoaïn maïch cda chòu taùc duïng cuûa töø löïc F2 taïo vôùi höôùng dòch chuyeån moät goùc nhoïn, neân coâng sinh ra coù daáu döông. Coâng naøy coù giaù trò baèng cöôøng ñoä doøng ñieän chaïy trong maïch, nhaân vôùi töø thoâng do phaàn maïch naøy queùt trong quaù trình di chuyeån, töùc laø: A2 = I (Φ0 + Φ2) (6-35) Coâng toaøn phaàn khi di chuyeån maïch kín coù giaù trò: A = A1 + A2 = I (Φ2 – Φ1) = IΔΦ (6-36) Keát quaû treân ñuùng cho tröôøng hôïp maïch kín di chuyeån trong moät töø tröôøng ñeàu baát kyø. Töø ñoù ta coù theå keát luaän: “Coâng cuûa löïc töø khi di chuyeån moät maïch ñieän kín trong töø tröôøng coù giaù trò baèng tích soá giöõa cöôøng ñoä doøng ñieän chaïy trong maïch vaø ñoä bieán thieân cuûa töø thoâng göûi qua dieän tích cuûa maïch kín. a’ a Φ2 Φ0 F2 b’ d’ Φ1 α2 b d u r ☼B F1 α1 c’ c Hình 6-17 6.5.3. Theá naêng cuûa maïch ñieän kín trong töø tröôøng. Maïch ñieän kín ñaët trong töø tröôøng seõ coù moät naêng löôïng xaùc ñònh, coù giaù trò baèng coâng ñeå mang noù vaøo trong töø tröôøng. Giaû söû ban ñaàu, maïch ôû voâ cöïc, töø tröôøng nôi ñoù baèng khoâng neân töø thoâng göûi qua maïch laø Φ1 = 0. Khi ôû trong töø tröôøng, töø thoâng göûi qua maïch seõ laø Φ2 = Φ. Coâng cuûa löïc töø ñöa maïch vaøo töø tröôøng laø: A = I (Φ2 – Φ1) = I Φ Coâng cuûa ngoaïi löïc caàn thöïc hieän coù daáu ngöôïc vôùi coâng cuûa löïc töø, neân coù giaù trò laø –IΦ. Coâng naøy bieán thaønh naêng löôïng W cuûa maïch ñieän: uu rr W = – IΦ = – IBS cos α = – P m B (6-37) Löu Theá Vinh

CÓ THỂ BẠN MUỐN DOWNLOAD
-

Giáo trình Di truyền học - Phạm Thành Hổ
 618 p |
618 p |  1757
|
1757
|  697
697
-

Giáo trình điện tử VI SINH VẬT HỌC CÔNG NGHIỆP
 202 p |
202 p |  712
|
712
|  428
428
-

Giáo trình Điện Hóa Học chương 1: Dung dịch chất điện li và lý thuyết điện ly Arrhesninus
 9 p |
9 p |  643
|
643
|  163
163
-

Giáo trình Điện Hóa Học chương 5: Nhiệt động học điện hóa
 33 p |
33 p |  454
|
454
|  159
159
-
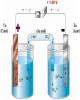
Giáo trình Điện Hóa Học chương 2: Tương tác Ion - Lưỡng cực dung môi trong các dung dịch điện ly
 7 p |
7 p |  374
|
374
|  106
106
-

Giáo trình Điện tử hạt nhân - Nguyễn Đức Hòa
 200 p |
200 p |  471
|
471
|  96
96
-

GIÁO TRÌNH ĐIỆN TỪ HỌC
 190 p |
190 p |  120
|
120
|  37
37
-

Giáo trình Di truyền học - Phạm Thành Hổ
 62 p |
62 p |  163
|
163
|  32
32
-

Giáo trình Điện tử học - Phần 1
 19 p |
19 p |  128
|
128
|  31
31
-

Giáo trình Điện tử học - Phần 2
 20 p |
20 p |  136
|
136
|  25
25
-

Điện từ học - TS. Lưu Thế Vinh
 190 p |
190 p |  115
|
115
|  23
23
-

Giáo trình điện từ học - TS. Lưu Thế Vinh - Chương 1
 28 p |
28 p |  131
|
131
|  16
16
-

ĐIỆN TỬ CÔNG SUẤT - CHƯƠNG 4 bộ biến đổi và bộ khóa một chiều
 31 p |
31 p |  170
|
170
|  16
16
-

Giáo trình điện từ học - TS. Lưu Thế Vinh - Chương 10
 33 p |
33 p |  126
|
126
|  8
8
-

Giáo trình Điện động lực học: Phần 1
 49 p |
49 p |  12
|
12
|  7
7
-

Giáo trình Điện động lực học: Phần 2
 52 p |
52 p |  20
|
20
|  7
7
-

Giáo trình Động lực học sông: Phần 2 - Nguyễn Thị Nga, Trần Thục
 264 p |
264 p |  13
|
13
|  5
5
-

Thiết kế và sử dụng giáo trình điện tử góp phần ôn tập củng cố kiến thức và phát triển năng lực dạy học cho sinh viên ngành sư phạm Hóa học
 10 p |
10 p |  97
|
97
|  4
4
Chịu trách nhiệm nội dung:
Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA
LIÊN HỆ
Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM
Hotline: 093 303 0098
Email: support@tailieu.vn








