Chöông trình Giaûng daïy Kinh teá Fulbright
Nieân khoùa 2003-2004 Phöông phaùp phaân tích
Baøi ñoïc Nhaäp moân kinh teá löôïng vôùi caùc öùng duïng
Chöông 2: OÂn laïi xaùc suaát vaø thoáng keâ
Ramu Ramanathan 25 Thuïc Ñoan/Haøo Thi
Trong phaàn naøy chuùng ta trình baøy hai thuû tuïc coù theå thay theá nhau ñeå öôùc löôïng
caùc thoâng soá chöa bieát cuûa phaân phoái xaùc suaát maø caùc quan saùt x1, x2, . . . , xn ñöôïc ruùt ra
töø ñoù. trong Phuï luïc, Phaàn 2.A.3, ta moâ taû theâm moät phöông phaùp naâng cao. trong phaàn
thaûo luaän tieáp theo, chuùng ta seõ giaû söû raèng nhaø khaûo saùt bieát ñöôïc baûn chaát cuûa phaân
phoái xaùc suaát nhöng chöa bieát caùc giaù trò cuûa caùc thoâng soá.
Phöông phaùp Momen
Phöông phaùp laâu ñôøi nhaát ñeå öôùc löôïng caùc thoâng soá laø phöông phaùp momen. Neáu moät
phaân phoái coù k thoâng soá chöa bieát, thuû tuïc nhaèm tính toaùn heä soá caùc momen maãu k baäc
nhaát cuûa phaân phoái vaø söû duïng chuùng nhö laø caùc öôùc löôïng cuûa caùc momen toång theå
töông öùng. Trong Phaàn 2.2, chuùng toâi ñaõ coù löu yù raèng trung bình toång theå cuûa phaân
phoái (µ) cuõng ñöôïc ñeà caäp ñeán nhö laø momen baäc nhaát cuûa phaân phoái xung quanh giaù trò
goác. Ñoù laø giaù trò trung bình coù troïng soá cuûa taát caû caùc x coù theå coù, caùc troïng soá laø caùc xaùc
suaát töông öùng. Trung bình maãu (x
_) laø trò trung bình soá hoïc cuûa caùc quan saùt maãu x1, x2, .
. . , xn . Baèng phöông phaùp caùc momen, x
_ ñöôïc tính nhö laø moät öôùc löôïng cuûa µ. Phöông
sai cuûa moät bieán ngaãu nhieân laø σ2 = E [(X – µ)2] vaø ñöôïc bieát nhö laø momen baäc hai xung
quanh giaù trò trung bình. Phöông sai maãu (s2), ñöôïc ñònh nghóa trong Phöông trình (2.9),
ñöôïc söû duïng nhö laø moät öôùc löôïng cuûa phöông sai toång theå cuûa phaân phoái. Trong nhieàu
tröôøng hôïp (ví duï nhö, phaân phoái chuaån), trung bình vaø phöông sai ñaëc tröng hoaøn toaøn
cho moät phaân phoái, vaø do ñoù khoâng coù nhu caàu phaûi söû duïng caùc momen baäc cao hôn nhö
laø giaù trò kyø voïng cuûa (X – µ)3. Chuùng ta seõ thaáy trong Phaàn 2.6 raèng trung bình maãu coù
moät soá tính chaát mong muoán.
Cuøng vôùi nguyeân lyù naøy coù theå ñöôïc aùp duïng ñeå öôùc löôïng heä soá cuûa söï töông quan
giöõa hai bieán ngaãu nhieân X vaø Y (xem Ñònh nghóa 2.5). Goïi x1, x2, . . . , xn vaø y1, y2, . . . ,
yn laø caùc maãu quan saùt ngaãu nhieân ñoäc laäp (vôùi côõ maãu n) töông öùng vôùi X vaø Y. Phöông
sai toång theå giöõa chuùng ñöôïc cho trong Ñònh nghóa 2.4 laø E [(X – µx) (Y – µy)], trong ñoù
µx vaø µy laø caùc trung bình toång theå töông öùng cuûa X vaø Y. Moät trò öôùc löôïng cuûa thoâng soá
naøy ñöôïc cho bôûi phöông sai maãu
S
xy = Cov(X, Y) = 1
n – 1 ∑ (xi – x
_) (yi – y
_) (2.10)
Neáu caùc caëp giaù trò cuûa xi vaø yi ñöôïc veõ ra ñoà thò, chuùng ta coù ñöôïc moät ñoà thò nhö
Hình 2.7, trong ñoù X vaø Y coù töông quan thuaän vôùi nhau (nghóa laø, X vaø Y noùi chung laø
cuøng dòch chuyeån theo cuøng moät höôùng). Chuùng ta ñaõ coù ñeà caäp raèng moät ñoà thò ñieåm
nhö vaäy ñöôïc goïi laø bieåu ñoà phaân taùn. Hình 2.6 cuõng töông töï nhö vaäy ngoaïi tröø vieäc
trung bình veõ nhöõng ñieåm ñeà caäp ñeán toång theå, trong khi ôû ñaây noù laïi ñeà caäp ñeán maãu.
Chöông trình Giaûng daïy Kinh teá Fulbright
Nieân khoùa 2003-2004 Phöông phaùp phaân tích
Baøi ñoïc Nhaäp moân kinh teá löôïng vôùi caùc öùng duïng
Chöông 2: OÂn laïi xaùc suaát vaø thoáng keâ
Ramu Ramanathan 26 Thuïc Ñoan/Haøo Thi
Baèng caùch chuyeån ñoåi caùc truïc thaønh caùc ñöôøng neùt ñöùt xuaát phaùt töø ñieåm (x
_,y
_), chuùng ta
coù theå thaáy raèng (xi – x
_) vaø (yi – y
_) laø nhöõng khoaûng caùch töø ñieåm trung bình (x
_,y
_).
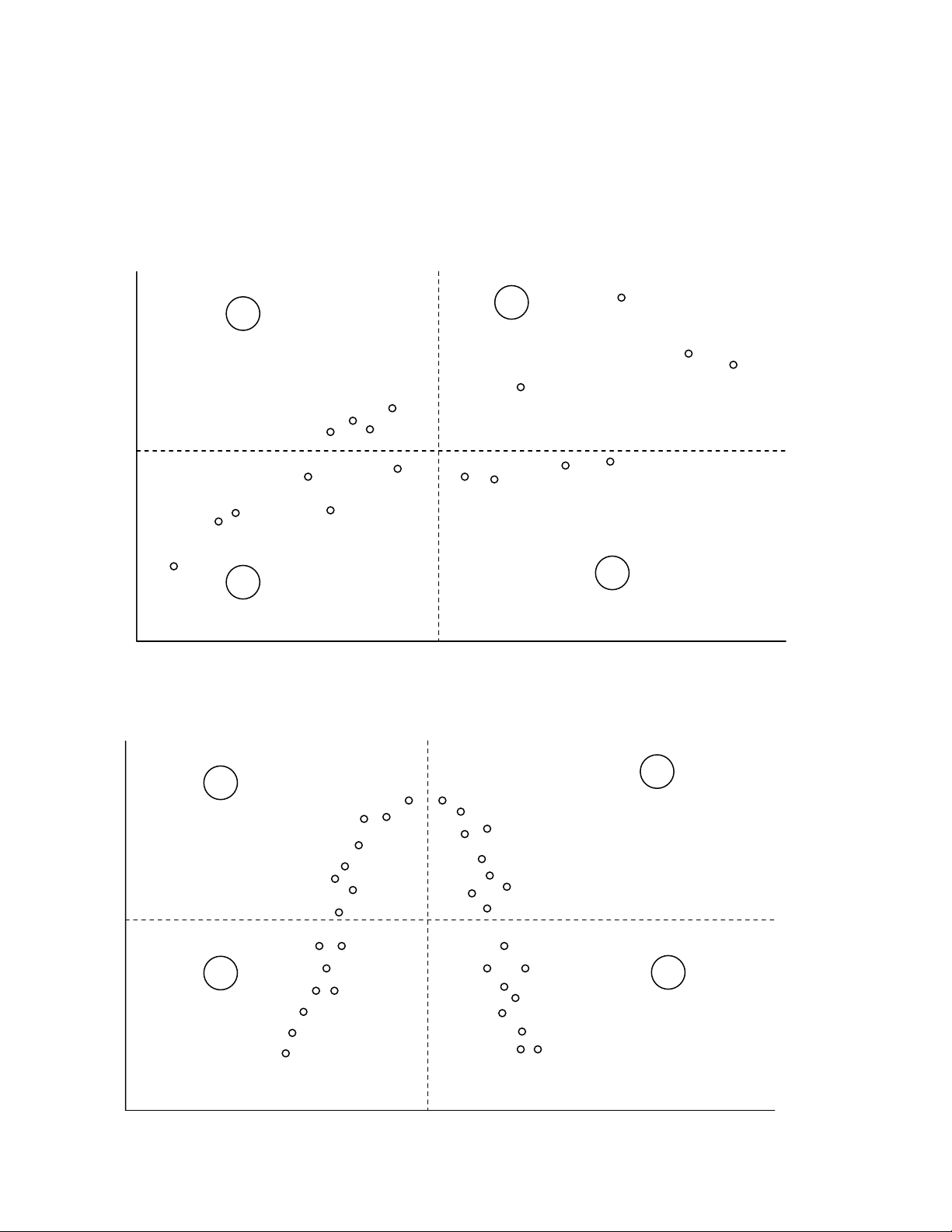
} Hình 2.7 Moät Bieåu ñoà Phaân taùn ñoái vôùi Töông quan Thuaän
} Hình 2.8 Moät Bieåu ñoà Phaân taùn ñoái vôùi Moái quan heä xaáp xæ baäc hai
0
y
_
x
_
Y
X
3
2 1
4
0
y
_
x
_
Y
X
3
2 1
4
Chöông trình Giaûng daïy Kinh teá Fulbright
Nieân khoùa 2003-2004 Phöông phaùp phaân tích
Baøi ñoïc Nhaäp moân kinh teá löôïng vôùi caùc öùng duïng
Chöông 2: OÂn laïi xaùc suaát vaø thoáng keâ
Ramu Ramanathan 27 Thuïc Ñoan/Haøo Thi
Neáu moái quan heä laø döông, chuùng ta seõ kyø voïng haàu heát caùc ñieåm ñeàu naèm trong
caùc phaàn tö thöù nhaát vaø thöù ba maø trong ñoù tích soá (xi – x
_) (yi – y
_) seõ döông. Do caùc tích
soá aâm cuûa caùc ñieåm trong phaàn tö thöù hai vaø thöù tö haàu nhö bò laán aùt bôûi caùc tích soá
döông, chuùng ta seõ kyø voïng ñoàng phöông sai laø döông. Baèng lyù luaän töông töï, chuùng ta
coù theå thaáy raèng neáu moái quan heä laø aâm, haàu heát caùc ñieåm seõ naèm trong phaàn tö thöù hai
vaø thöù tö, taïo ra moät ñoàng phöông sai aâm. Ñieàu naøy cho thaáy raèng neáu X vaø Y coù töông
quan thuaän, thì ñoàng phöông sai vaø do ñoù töông quan giöõa chuùng cuõng seõ thuaän. Moät moái
quan heä aâm seõ cho moät heä soá töông quan aâm. Heä soá töông quan maãu ñöôïc cho bôûi
r
xy = sxy
sxsy = ∑ (xi – x
_) (yi – y
_)
[∑ (xi – x
_)2]1/2 [∑ (yi – y
_)2]1/2 (2.11)
trong ñoù sx vaø sy laø caùc ñoä leäch chuaån maãu (caên baäc hai cuûa caùc phöông sai) töông öùng
cuûa X vaø Y.
Trong Phaàn 2.3 chuùng ta ñaõ coù ñeà caäp ñeán vaán ñeà heä soá töông quan laø moät ñaïi
löôïng ño löôøng moái quan heä tuyeán tính giöõa X vaø Y. Hình 2.8 laø moät bieåu ñoà phaân taùn
cho ta thaáy tröôøng hôïp khi Y laø moät haøm xaáp xæ baäc hai cuûa X. chuùng toâi löu yù raèng caùc
ñieåm ñöôïc phaân taùn trong caû boán phaàn tö cuûa bieåu ñoà, vaø do ñoù toång ∑ (xi – x
_) (yi – y
_)
haàu nhö raát nhoû, cho moät giaù trò rxy nhoû. Vì vaäy, moät rxy nhoû khoâng coù nghóa laø X vaø Y
khoâng coù quan heä chaët cheõ vôùi nhau, maø coù nghóa laø chuùng khoâng coù quan heä tuyeán tính
chaët cheõ.
Baøi taäp 2.24 minh hoïa khaùi nieäm söï töông quan ñöôïc aùp duïng cho ñöôøng cong
Phillips.
Ñoái vôùi nhöõng ngöôøi söû duïng GRETL, Phaàn Thöïc haønh treân Maùy tính 2.3 (xem Phuï
luïc D, Baûng D.1) chöùng toû raèng vieäc tính toaùn caùc ñoàng phöông sai vaø töông quan giöõa
ñieåm trung bình ôû ñaïi hoïc vaø ñieåm trung bình ôû trung hoïc theo döõ lieäu trong DATA 2-2,
ñöôïc moâ taû trong Phuï luïc D. Haõy söû duïng chöông trình rieâng cuûa baïn vôùi DATA 2-2 ñeå
xaùc minh laïi caùc keát quaû ñöôïc trình baøy ôû ñaây.
} Baûng 2.8 Soá lieäu Keát quaû töø Maùy tính ñöôïc giaûi thích töøng phaàn minh hoïa cho caùc trò thoáng
keâ toùm taét khaùc nhau.
Caùc chuù giaûi ñöôïc qui ñònh ôû daïng rieâng khaùc vôùi daïng ñöôïc söû duïng cho caùc keát quaû
maùy tính.
x = colgpa = Grade point average in College
y = hsgpa = Grade point average in High School
Correlation between x and y = 0.406662
Summary Statistics, using the observations 1 – 427
Chöông trình Giaûng daïy Kinh teá Fulbright
Nieân khoùa 2003-2004 Phöông phaùp phaân tích
Baøi ñoïc Nhaäp moân kinh teá löôïng vôùi caùc öùng duïng
Chöông 2: OÂn laïi xaùc suaát vaø thoáng keâ
Ramu Ramanathan 28 Thuïc Ñoan/Haøo Thi
Variable MEAN MEDIAN MIN MAX
x 2.7855 2.79 0.85 3.97
y 3.55785 3.59 2.29 4.5
Variable S.D. C.V. SKEW EXCSKURT
x 0.54082 0.194155 -0.203647 -0.0517458
y 0.419577 0.11793 -0.401241 -0.220107
Min vaø Max laø nhöõng giaù trò nhoû nhaát vaø lôùn nhaát trong maãu. Median laø giaù trò cuûa
x hoaëc y tính theo moãi beân cuûa giaù trò naøy seõ coù 50% caùc quan saùt. C.V. laø heä soá bieán
thieân (MEAN/S.D.) ñaõ ñöôïc thaûo luaän trong Phaàn 2.2. SKEW laø moät ñaïi löôïng ño löôøng
söï phaân phoái cuûa bieán sai leäch bao xa so vôùi ñieåm ñoái xöùng (trong baøi naøy goïi laø ñoä leäch
skewness). Moät giaù trò baèng khoâng cho bieát ñieåm ñoái xöùng xung quanh giaù trò khoâng.
Moät giaù trò döông cho bieát ñoä leäch veà beân phaûi vôùi moät nhaùnh daøi theo höôùng naøy. Moät
giaù trò aâm cho bieát ñoä leäch ñoái xöùng skewness sang beân traùi vôùi moät nhaùnh daøi theo
höôùng naøy. EXCKURT laø ñoä leäch kurtosis, nghóa laø, ñoä kurtosis –3. Kurtosis laø moät ñaïi
löôïng ño löôøng ñoä roäng hình choùp cuûa moät phaân phoái. Phaân phoái chuaån coù kurtosis laø 3.
Moät phaân phoái daøn traûi roäng seõ coù moät giaù trò kurtosis aâm, vaø moät phaân phoái heïp seõ coù
moät giaù trò kurtosis döông. Ñoä leäch skewness vaø kurtosis khoâng ñöôïc thaûo luaän trong baøi
vì chuùng khoâng ñöôïc söû duïng nhieàu trong kinh teá löôïng. Neáu muoán bieát theâm chi tieát veà
caùc ñaïi löôïng naøy, haõy xem saùch cuûa Ramanathan (1993, Phaàn 3.5).
Moät phieân baûn giaûi thích keát quaû ñöôïc trình baøy ôû Baûng 2.8. Baûng cuõng cung caáp
theâm caùc ñaïi löôïng thoáng keâ toùm taét chöa ñöôïc thaûo luaän ôû phaàn treân.
Phöông Phaùp Bình Phöông Toái Thieåu (hay Bình Phöông Toái Thieåu Thoâng Thöôøng)
Trong kinh teá löôïng, phöông phaùp ñöôïc söû duïng phoå bieán nhaát ñeå öôùc löôïng caùc thoâng soá
laø phöông phaùp bình phöông toái thieåu (cuõng coøn ñöôïc bieát ñeán döôùi teân bình phöông toái
thieåu thoâng thöôøng hay OLS). Maëc duø noù ñöôïc söû duïng chuû yeáu ñeå öôùc löôïng caùc thoâng
soá cuûa moät moâ hình hoài qui daïng PRICE =
α
+
β
SQFT + u ñaõ gaëp phaûi trong Chöông 1,
phöông phaùp naøy coøn raát höõu ích trong tröôøng hôïp öôùc löôïng giaù trò trung bình cuûa moät
bieán ñôn ngaãu nhieân X.
Töøng quan saùt xi coù theå ñöôïc xem nhö moät giaù trò öôùc löôïng cuûa maãu trung bình
µ
vì
E(xi) =
µ
. Sai soá trong giaù trò öôùc löôïng naøy laø ei = xi –
µ
(töùc laø, xi =
µ
+ ei). Xem xeùt
toång bình phöông cuûa sai soá naøy trong toång theå maãu. Töùc laø, ñaët ESS (
µ
) = ∑2
i
e= ∑ (xi –
µ
)2. Phöông phaùp bình phöông toái thieåu choïn giaù trò öôùc löôïng
µ
maø toång bình phöông sai
soá maãu laø nhoû nhaát. Vieäc bình phöông caùc sai soá giaûi quyeát ñöôïc hai vaán ñeà. Ñaàu tieân, noù
loaïi boû daáu cuûa sai soá. Vì vaäy, nhöõng sai soá coù giaù trò döông vaø aâm ñöôïc xem xeùt nhö
nhau. Thöù hai, vieäc bình phöông seõ loaïi boû nhöõng sai soá lôùn bôûi vì nhöõng sai soá nhö theá
bò phoùng ñaïi leân nhieàu khi laáy bình phöông.
Chöông trình Giaûng daïy Kinh teá Fulbright
Nieân khoùa 2003-2004 Phöông phaùp phaân tích
Baøi ñoïc Nhaäp moân kinh teá löôïng vôùi caùc öùng duïng
Chöông 2: OÂn laïi xaùc suaát vaø thoáng keâ
Ramu Ramanathan 29 Thuïc Ñoan/Haøo Thi
Ñeå coù ñöôïc
µ
ˆ, öôùc löôïng
µ
baèng caùch toái thieåu ESS, vieát ESS nhö sau:
ESS (
µ
ˆ) = ∑ (xi –
µ
ˆ)2 = ∑ (xi –
x
+
x
–
µ
ˆ)2
= ∑ (xi –
x
)2 + ∑ (
x
–
µ
ˆ)2 + 2∑ (
x
–
µ
ˆ)(xi –
x
)
= ∑ (xi –
x
)2 + ∑ (
x
–
µ
ˆ)2
Bôûi vì
x
–
µ
ˆ trong soá haïng thöù ba laø moät haèng soá, neân noù coù theå ñöôïc loaïi ra (xem Phuï
Luïc 2.A.1) vaø, theo Tính Chaát 2.A.4, soá haïng thöù ba baèng khoâng. Do trong soá haïng ñaàu
khoâng coù
µ
ˆ, neân chuùng ta thaáy raèng ESS ñöôïc toái thieåu ñoái vôùi vieäc löïa choïn
µ
ˆ neáu vaø
chæ neáu chuùng ta cho
µ
ˆ =
x
, ñieàu naøy noù coù theå laøm cho soá haïng thöù hai baèng khoâng. Do
ñoù, giaù trò öôùc löôïng bình phöông toái thieåu cuûa
µ
laø giaù trò trung bình maãu
x
.
Trong phaàn phuï luïc cuûa chöông, chuùng ta seõ thaûo luaän moät thuû tuïc khaùc, hieän ñaïi
hôn: giaù trò öôùc löôïng thích hôïp cöïc ñaïi (MLE). Nhöõng ngöôøi ñoïc coù quan taâm neân ñoïc
phaàn naøy.
(Ñeå thaáy ñöôïc vieäc söû duïng nhöõng phöông phaùp dieãn taû trong phaàn naøy trong öôùc
löôïng caùc hoài qui nhö theá naøo, xem tieáp Phaàn 3.1 vaø 3.2.)
} 2.6 Caùc Tính Chaát Cuûa Öôùc Löôïng
Trong phaàn tröôùc chuùng ta ñaõ thaûo luaän hai thuû tuïc öôùc löôïng maø noù choïn trung bình maãu
laø öôùc löôïng cuûa
µ
. Trong ví duï chieàu cao cuûa ngöôøi trong Phaàn 2.5, moät öôùc löôïng thay
theá ñoù laø laáy caùc chieàu cao cuûa nhöõng ngöôøi cao nhaát vaø nhöõng ngöôøi thaáp nhaát vaø laáy
trung bình. Öôùc löôïng naøo toát hôn? Ñeå coù theå traû lôøi ñöôïc nhöõng caâu hoûi loaïi nhö theá
naøy, chuùng ta caàn moät vaøi tieâu chí trong vieäc choïn löïa giöõa nhöõng öôùc löôïng khaùc nhau.
Moät vaøi tieâu chuaån ñaõ ñöôïc thieát laäp ñeå ñaùnh giaù “söï thích hôïp” cuûa moät öôùc löôïng,
nhöng trong nhöõng phaàn sau chuùng ta chæ thaûo luaän caùc khaùi nieäm ñöôïc söû duïng thöôøng
xuyeân nhaát trong kinh teá löôïng. Moät vaøi khaùi nieäm trong ñoù aùp duïng ñöôïc cho nhöõng côõ
maãu nhoû vaø nhöõng khaùi nieäm khaùc chæ thích hôïp ñoái vôùi nhöõng côõ maãu lôùn.
Nhöõng Tính Chaát Cuûa Öôùc Löôïng Côõ Maãu Nhoû
Kyù hieäu chuaån cho thoâng soá chöa bieát laø
θ
vaø kyù hieäu moät giaù trò öôùc löôïng laø
θ
ˆ. Neân
nhaán maïnh raèng
θ
ˆ laø moät haøm soá cuûa nhöõng quan saùt x1, x2, … , xn vaø noù khoâng phuï thuoäc
vaøo baát kyø thoâng soá chöa bieát naøo. Do ñoù moät giaù trò öôùc löôïng nhö vaäy laø moät trò thoáng
keâ maãu. Tuy nhieân, bôûi vì x laø nhöõng bieán ngaãu nhieân, neân
θ
ˆ cuõng ngaãu nhieân.
KHOÂNG THIEÂN LEÄCH Bôûi vì
θ
ˆ laø moät bieán ngaãu nhieân, neân noù coù moät phaân phoái xaùc
suaát vôùi giaù trò trung bình naøo ñoù, goïi laø E(
θ
ˆ). Neáu giaù trò trung bình naøy töông ñöông