Gi¸o tr×nh M« h×nh ho¸
Bé m«n Tù ®éng ho¸ http://www.ebook.edu.vn Khoa §iÖn
21
Ch−¬ng 3- M« pháng hÖ thèng liªn tôc
3.1- Kh¸i niÖm chung vÒ m« h×nh hÖ thèng liªn tôc
HÖ thèng liªn tôc lµ hÖ thèng mµ trong ®ã c¸c tr¹ng th¸i vµ thuéc tÝnh cña hÖ thay ®æi
mét c¸ch liªn tôc. M« h×nh to¸n häc cña hÖ thèng liªn tôc th−êng lµ ph−¬ng tr×nh vi ph©n.
Tr−êng hîp ®¬n gi¶n nhÊt ®ã lµ hÖ ph−¬ng tr×nh vi ph©n tuyÕn tÝnh hÖ sè h»ng vµ ®−îc gi¶i
mét c¸ch dÔ dµng b»ng ph−¬ng ph¸p gi¶i tÝch. Tuy nhiªn, khi m« h×nh cã phÇn tö phi tuyÕn
nh− phÇn tö b·o hoµ, phÇn tö trÔ, phÇn tö cã vïng chÕt,... th× ph−¬ng ph¸p gi¶i tÝch khã hoÆc
kh«ng thÓ gi¶i ®−îc. Trong tr−êng hîp nµy hîp lý nhÊt lµ dïng ph−¬ng ph¸p m« pháng ®Ó gi¶i
bµi to¸n. ng−êi ta cã thÓ dïng m¸y tÝnh t−¬ng tù hoÆc m¸y tÝnh sè ®Ó m« pháng hÖ thèng liªn
tôc.
3.2- Dïng m¸y tÝnh t−¬ng tù ®Ó m« pháng hÖ thèng liªn tôc
M¸y tÝnh t−¬ng tù ®· cã qu¸ tr×nh ph¸t triÓn l©u dµi vµ ®· gãp phÇn gi¶i c¸c bµi to¸n cña
hÖ thèng liªn tôc tuyÕn tÝnh còng nh− phi tuyÕn. M¸y tÝnh t−¬ng tù ®−îc dïng rÊt réng r·i nhÊt
lµ m¸y tÝnh t−¬ng tù ®iÖn tö mµ phÇn tö c¬ b¶n cña nã lµ c¸c bé khuÕch ®¹i thuËt to¸n
OPAMP (Operational Amplifier). §iÖn ¸p cña m¸y tÝnh biÓu thÞ biÕn sè m« h×nh to¸n häc.
KhuÕch ®¹i thuËt to¸n cã thÓ lµm thµnh c¸c bé céng, tÝch ph©n vµ bé ®¶o dÊu ®iÖn ¸p do ®ã nã
cã thÓ gi¶i c¸c ph−¬ng tr×nh vi ph©n dïng ®Ó m« h×nh ho¸ hÖ thèng liªn tôc. M¸y tÝnh t−¬ng tù
bÞ h¹n chÕ bëi ®é chÝnh x¸c kh«ng cao do nhiÒu nguyªn nh©n: do ®é chÝnh x¸c cña phÐp ®o
®iÖn ¸p, do hiÖn t−îng tr«i ®iÓm kh«ng cña khuÕch ®¹i thuËt to¸n,... Nãi chung, ®é chÝnh x¸c
cña m¸y tÝnh t−¬ng tù kh«ng v−ît qu¸ 0,1%. Mét h¹n chÕ quan träng kh¸c cña m¸y tÝnh t−¬ng
tù lµ ®èi víi tõng hÖ thèng cô thÓ ph¶i l¾p r¸p vµ hiÖu chØnh m¸y tÝnh, h¬n n÷a m¸y tÝnh kh«ng
cã kh¶ n¨ng ph¸t triÓn mÒm dÎo khi muèn thay ®æi cÊu tróc cña hÖ thèng. Tõ khi cã m¸y tÝnh
sè, m¸y tÝnh t−¬ng tù Ýt ®−îc sö dông vµo m« pháng. Tuy nhiªn m¸y tÝnh t−¬ng tù cßn ®−îc sö
dông trong mét sè tr−êng hîp nh− lµm thiÕt bÞ m« pháng cña hÖ thèng s¶n xuÊt ho¸ chÊt, sinh
häc hoÆc dïng trong m« pháng hçn hîp. XÐt mét hÖ thèng liªn tôc ®−îc m« h×nh ho¸ b»ng
ph−¬ng tr×nh vi ph©n tuyÕn tÝnh sau:
2
2
dx dx
BxF(t)
dt dt
++= (3.1)
Gi¶ thiÕt r»ng c¸c ®iÒu kiÖn ®Çu b»ng kh«ng vµ c¸c hÖ sè trong ph−¬ng tr×nh vi ph©n ®Òu
lµ h»ng sè.
Víi B > 1, cã thÓ viÕt (3.1) thµnh ph−¬ng tr×nh sau:
xBxxF(t)=− − +
&& & (3.2)
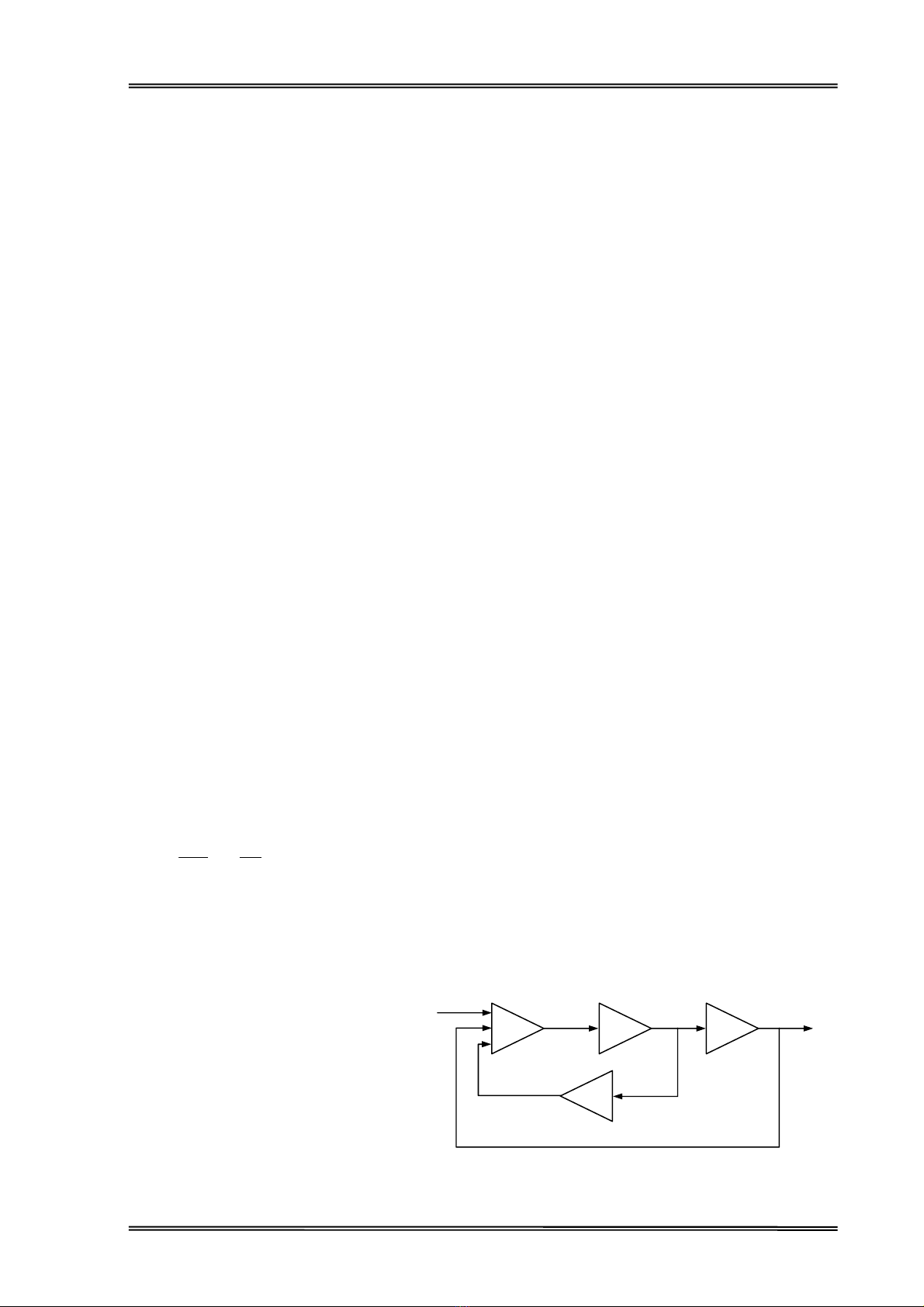
Dùa vµo ph−¬ng tr×nh (3.2)
ta cã thÓ x©y dùng ®−îc s¬ ®å
khèi cña m¸y tÝnh t−¬ng tù nh−
h×nh 3.1 ®Ó gi¶i ph−¬ng tr×nh
trªn.
§Ó nhËn ®−îc ®¸p øng cña
hÖ thèng ng−êi ta ph¶i ®Æt tÝn
hiÖu F(t) vµo bé céng. Qua hai
B
F(t) x
&& x
&x
H×nh 3.1- S¬ ®å khèi cña m¸y tÝnh t−¬ng tù ®Ó gi¶i
ph−¬ng tr×nh vi ph©n (3.2)
Gi¸o tr×nh M« h×nh ho¸
Bé m«n Tù ®éng ho¸ http://www.ebook.edu.vn Khoa §iÖn
22
khèi tÝch ph©n ta nhËn ®−îc tÝn hiÖu ta x, tøc lµ lêi gi¶i cña ph−¬ng tr×nh. HiÖu chØnh hÖ sè B
®Ó ®−îc ®Æc tÝnh ra mong muèn.
3.3- Dïng m¸y tÝnh sè ®Ó m« pháng hÖ thèng liªn tôc
Tõ khi m¸y tÝnh sè ra ®êi ®Õn nay ®· h¬n nöa thÕ kû, m¸y tÝnh sè ®· ph¸t triÓn rÊt nhanh
vµ ®−îc øng dông vµo hÇu hÕt c¸c lÜnh vùc ho¹t ®éng cña con ng−êi. Do ngµy nay chñ yÕu
dïng m¸y tÝnh sè nªn tõ ®©y vÒ sau thuËt ng÷ m¸y tÝnh sè ®−îc gäi t¾t lµ m¸y tÝnh MT
(computer). Trong lÜnh vùc m« h×nh ho¸, m¸y tÝnh lµ c«ng cô chñ yÕu ®Ó thùc hiÖn viÖc m«
pháng hÖ thèng. Sau ®©y chóng ta sÏ nghiªn cøu m¸y tÝnh lµm viÖc nh− thÕ nµo trong viÖc m«
h×nh ho¸ hÖ thèng.
3.3.1- Ph−¬ng tr×nh m¸y tÝnh
Dïng m¸y tÝnh ®Ó m« h×nh ho¸ hÖ thèng cã nghÜa lµ ®−a vµo m¸y tÝnh c¸c d÷ liÖu ban
®Çu, m¸y tÝnh xö lý c¸c d÷ liÖu ®ã theo chøc n¨ng ho¹t ®éng cña hÖ thèng S, ®Çu ra cña m¸y
tÝnh cho ta c¸c tr¹ng th¸i cña hÖ thèng S theo thêi gian.
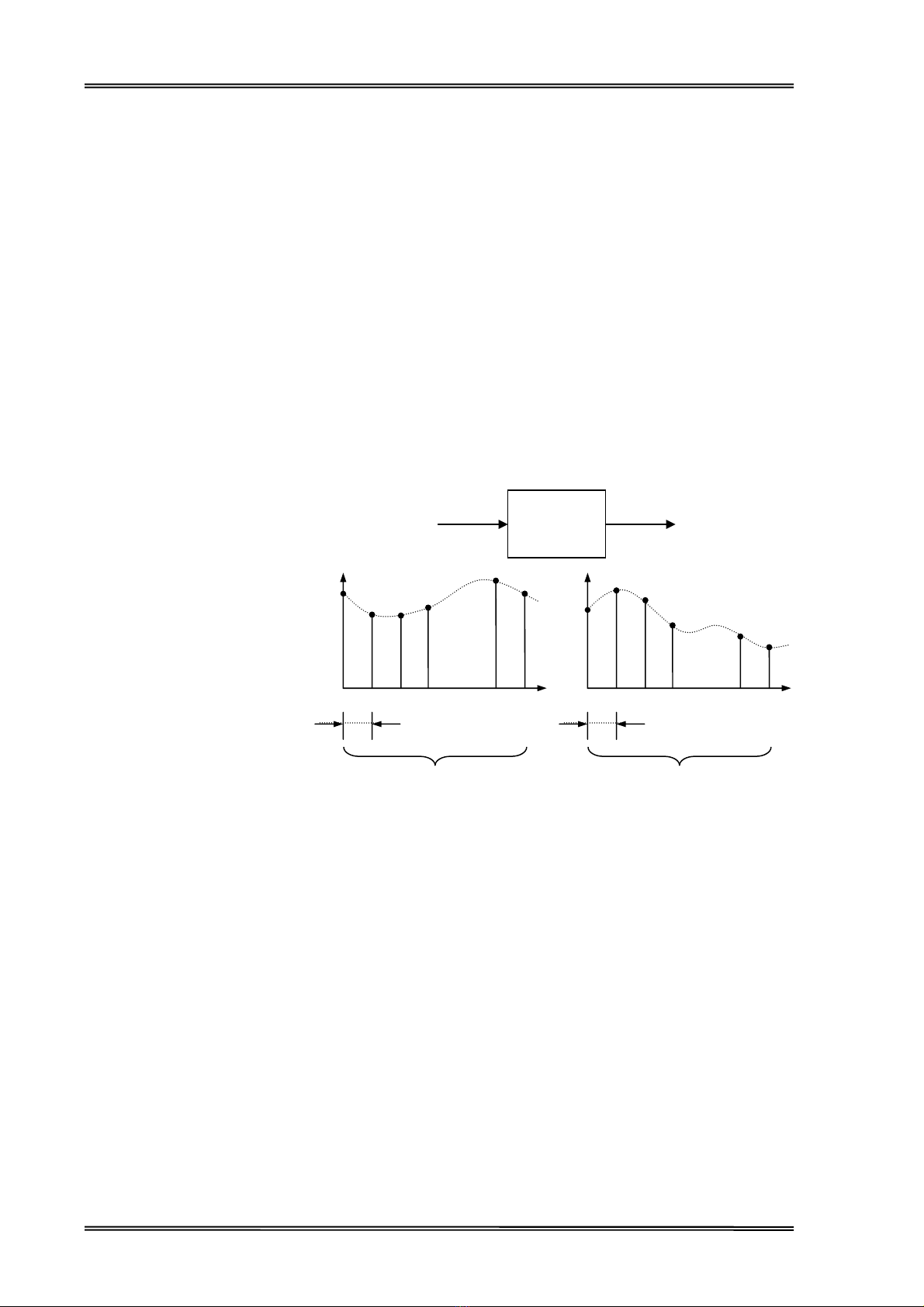
TÝn hiÖu vµo [Xk] vµ
tÝn hiÖu ra [Yk] cña m¸y
tÝnh ®Òu lµ nh÷ng tÝn hiÖu
sè (gi¸n ®o¹n). Sau ®©y ta
sÏ xÐt quan hÖ gi÷a chóng.
B−íc gi¸n do¹n ho¸
T (B−íc c¾t mÉu hay chu
kú c¾t mÉu) lµ nhÞp lµm
viÖc cña m¸y tÝnh.
D·y tÝn hiÖu vµo
[Xk] = [x(0), x(T),
x(2T),..., x(kT)].
D·y tÝn hiÖu ra
[Yk] = [y(0), y(T),
y(2T),..., y(kT)].
Khi kh¶o s¸t ta chÊp nhËn gi¶ thiÕt lµ thêi gian tÝnh to¸n cña m¸y tÝnh kh«ng ®¸ng kÓ
nªn cã thÓ bá qua, cã nghÜa lµ d·y tÝn hiÖu ra [Yk] hoµn toµn ®ång bé víi d·y tÝn hiÖu vµo
[Xk].
TÝn hiÖu ra ë thêi ®iÓm k tøc y(kT) phô thuéc vµo gi¸ trÞ cña n tÝn hiÖu ra vµ m+1 tÝn
hiÖu vµo x¶y ra tr−íc ®ã. C¸c gi¸ trÞ cña m tÝn hiÖu vµo vµ n tÝn hiÖu ra ®−îc l−u tr÷ trong bé
nhí cña m¸y tÝnh. Nh− vËy, quan hÖ gi÷a tÝn hiÖu ra vµ tÝn hiÖu vµo cña m¸y tÝnh ®−îc viÕt
nh− sau:
mn
mi n j
i0 j0
y(kT) b x(kT iT) a y(kT jT)
−−
==
=−−−
∑∑
(3.3)
trong ®ã an, bm – c¸c hÖ sè
i = 0 ÷ m, j = 0 ÷ n víi m < n.
Ph−¬ng tr×nh (3.3) ®−îc gäi lµ ph−¬ng tr×nh m¸y tÝnh, biÓu thÞ mèi quan hÖ tuyÕn tÝnh
gi÷a tÝn hiÖu vµo vµ tÝn hiÖu ra cña m¸y tÝnh.
MT
[Xk][Y
k]
kk-1 20
[Yk]
t
T
n +1
kk-120
[Xk]
t
T
m +1
H
×nh
3
.
2
- Quan hÖ gi÷a tÝn hiÖu vµo vµ ra cña m¸y tÝnh
Gi¸o tr×nh M« h×nh ho¸
Bé m«n Tù ®éng ho¸ http://www.ebook.edu.vn Khoa §iÖn
23
Chó ý r»ng trong ph−¬ng tr×nh (3.3) lu«n lu«n cã quan hÖ m ≤ n cã nghÜa lµ tÝn hiÖu ra
phô thuéc vµo m tÝn hiÖu vµo trong qu¸ khø. NÕu m > n cã nghÜa lµ tÝn hiÖu ra phô thuéc c¶
vµo (m – n) tÝn hiÖu vµo trong t−¬ng lai lµ ®iÒu kh«ng x¶y ra trong thùc tÕ ®−îc.
V× tÝn hiÖu ra [yk] vµ tÝn hiÖu vµo [xk] ®Òu cã cïng b−íc gi¸n ®o¹n T (chu kú c¾t mÉu)
nªn ®Ó cho gän ph−¬ng tr×nh (3.3) cã thÓ ®−îc viÕt l¹i nh− sau:
mn
mi n j
i0 j0
y(k) b x(k i) a y(k j)
−−
==
=−−−
∑∑
(3.4)
Ph−¬ng tr×nh (3.4) cã thÓ khai triÓn thµnh:
any(k)+an-1y(k-1)+...+ aoy(k-n) = bmx(k)+bm-1x(k-1)+...+ box(k-m) (3.5)
Ph−¬ng tr×nh (3.5) cã d¹ng ph−¬ng tr×nh sai ph©n bËc n.
C¸c hÖ sè an-1,..., a0 vµ bm,..., b0 ®Æc tr−ng cho ®Æc tÝnh ®éng cña hÖ thèng. NÕu c¸c hÖ sè
lµ h»ng sè th× ta cã ph−¬ng tr×nh sai ph©n tuyÕn tÝnh ph¶n ¸nh hÖ dõng (®Æc tÝnh kh«ng biÕn
®æi theo thêi gian), trong tr−êng hîp ng−îc l¹i ai (i = 0 ÷ n), bj (j = 0 ÷ m) biÕn ®æi theo thêi
gian – hÖ kh«ng dõng. Trong néi dung gi¸o tr×nh nµy, ta chØ kh¶o s¸t c¸c hÖ thèng tuyÕn tÝnh
dõng.
BËc cña ph−¬ng tr×nh sai ph©n lµ hiÖu gi÷a bËc cña sè h¹ng tÝn hiÖu ra lín nhÊt vµ bÐ
nhÊt. Trong tr−êng hîp ph−¬ng tr×nh (3.5), bËc cña ph−¬ng tr×nh lµ:
k – (k – n) = n
VËy ta cã thÓ kÕt luËn r»ng ph−¬ng tr×nh m¸y tÝnh cã d¹ng cña ph−¬ng tr×nh sai ph©n
tuyÕn tÝnh.
Tõ ph−¬ng tr×nh (3.5) ta cã thÓ viÕt:
y(k) = - an-1y(k-1) - ... - aoy(0) + bmx(k) + ... + box(0) (3.6)
nh− vËy nÕu biÕt ®iÒu kiÖn ®Çu x(0), y(0), b»ng c¸ch t¨ng dÇn b−íc k ta cã thÓ tÝnh ®−îc
y(k) ë c¸c thêi ®iÓm kh¸c nhau. C¸c kÕt qu¶ tÝnh to¸n ®−îc l−u tr÷ trong bé nhí cña m¸y tÝnh
vµ gi¸ trÞ tÝn hiÖu ra cña b−íc tiÕp theo phô thuéc vµo gi¸ trÞ cña tÝn hiÖu vµo vµ tÝn hiÖu ra
trong qu¸ khø.
3.3.2- Ph−¬ng ph¸p m« pháng hÖ liªn tôc tuyÕn tÝnh b»ng m¸y tÝnh sè
Tõ c¸c ph©n tÝch ë trªn ta thÊy r»ng muèn dïng m¸y tÝnh sè ®Ó m« pháng hÖ liªn tôc,
cÇn ph¶i m« t¶ hÖ d−íi d¹ng ph−¬ng tr×nh sai ph©n tuyÕn tÝnh sau ®ã ®−a ph−¬ng tr×nh sai
ph©n tuyÕn tÝnh ®ã vµo m¸y tÝnh ®Ó t×m c¸c ®Æc tÝnh m« pháng hÖ liªn tôc.
Chó ý r»ng hÖ liªn tôc th−êng ®−îc biÓu diÔn b»ng ph−¬ng tr×nh vi tÝch ph©n. §Ó biÕn
®æi ph−¬ng tr×nh vi tÝch ph©n thµnh ph−¬ng tr×nh sai ph©n t−¬ng øng cã thÓ dïng ph−¬ng ph¸p
sè Runge-Kutta. Tuy nhiªn, ph−¬ng ph¸p nµy cã khèi l−îng tÝnh to¸n lín, ®Æc biÖt lµ ®èi víi
ph−¬ng tr×nh cã bËc 3 trë lªn th× tÝnh to¸n rÊt phøc t¹p nhiÒu khi kh«ng thùc hiÖn ®−îc. V×
vËy, ë phÇn tiÕp theo sÏ tr×nh bµy mét ph−¬ng ph¸p tiÖn dông ®Ó t×m ph−¬ng tr×nh sai ph©n cña
hÖ liªn tôc. Tõ ph−¬ng tr×nh Laplace cña hÖ liªn tôc, b»ng c¸ch biÕn ®æi Z t−¬ng øng råi t×m
ng−îc l¹i ph−¬ng tr×nh sai ph©n cña hÖ ®Ó gi¶i trªn m¸y tÝnh sè.
3.4- BiÕn ®æi Z vµ c¸c tÝnh chÊt
- Môc ®Ých cña phÐp biÕn ®æi Z.
Khi gi¶i ph−¬ng tr×nh sai ph©n bËc cao ng−êi ta th−êng gÆp nhiÒu khã kh¨n, v× vËy
ng−êi ta th−êng dïng biÕn ®æi Z ®Ó biÕn ph−¬ng tr×nh sai ph©n tuyÕn tÝnh cña hÖ gi¸n ®o¹n
Gi¸o tr×nh M« h×nh ho¸
Bé m«n Tù ®éng ho¸ http://www.ebook.edu.vn Khoa §iÖn
24
thµnh ph−¬ng tr×nh ®¹i sè. §iÒu nµy hoµn toµn t−¬ng tù nh− trong tr−êng hîp hÖ liªn tôc dïng
biÕn ®æi Laplace ®Ó biÕn ph−¬ng tr×nh vi tÝch ph©n thµnh ph−¬ng tr×nh ®¹i sè.
- Mét sè ®Þnh nghÜa trong phÐp biÕn ®æi Z.
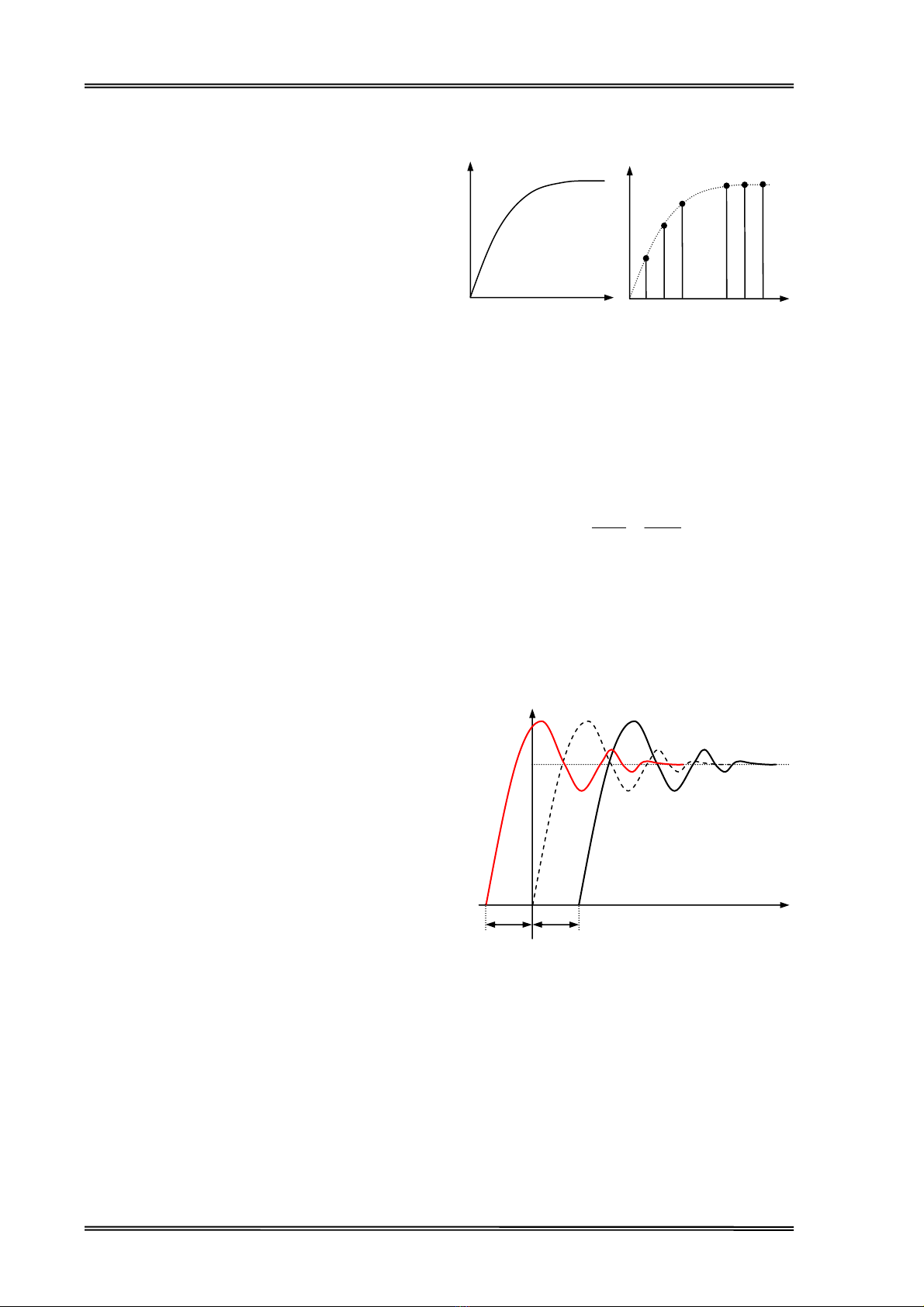
Gi¶ thiÕt r»ng kh«ng cã tÝn hiÖu ë phÝa ©m
cña trôc thêi gian (h×nh 4.2).
§èi víi tÝn hiÖu d¹ng liªn tôc x(t) ta cã
®Þnh nghÜa vÒ phÐp biÕn ®æi Laplace nh− sau:
∞
−
==
∫st
0
L[x(t)] X(s) x(t)e dt
(3.7)
§èi víi tÝn hiÖu gi¸n ®o¹n x[k] ta cã ®Þnh nghÜa vÒ phÐp biÕn ®æi Z nh− sau:
∞
−
−−
== + ++ =
∑
o1 k k
0
Z[x(k)] X(Z) X(0)Z X(1)Z ... x(k)Z x(k)Z (3.8)
trong ®ã Z lµ biÕn phøc.
NÕu hµm x(t) kh«ng tån t¹i, biÕn ®æi Laplace cã d¹ng: ==
B(s) B(p)
X(s) A(s) A(p)
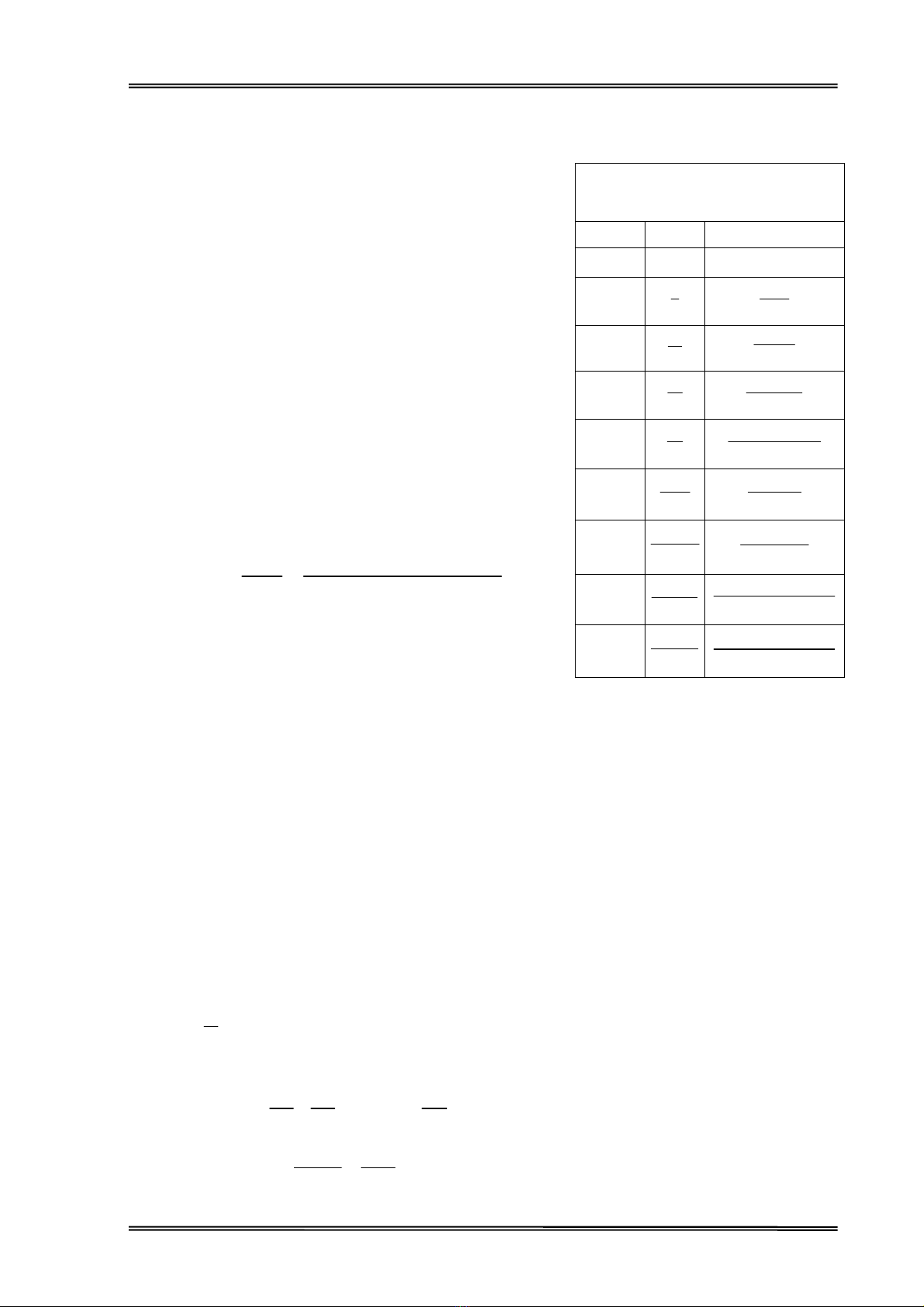
Th× chuçi (3.8) lµ biÕn ®æi Z cña hµm gi¸n ®o¹n x[k] t−¬ng øng. B¶ng 4.1 liÖt kª biÕn
®æi Laplace vµ biÕn ®æi Z cña mét sè hµm th«ng dông.
- C¸c tÝnh chÊt cña biÕn ®æi Z.
1. TÝnh chÊt tuyÕn tÝnh
Z{a.[v(k)] + b.[w(k)]} = a.V(z) + b.W(z) (3.9)
2. DÞch hµm gèc g(k) vÒ phÝa tr−íc m b−íc
mj
mj
j0
Z[f (k m)] zF(z) f (k)z
−−
=
+= −
∑ (3.10)
Víi ®iÒu kiÖn ®Çu b»ng 0 ta cã:
Z[f(k+m)]=zmF(z) (3.11)
3. DÞch hµm gèc g(k) vÒ phÝa sau m b−íc
Z[f(k - m)]=z-mF(z) (3.12)
4. BiÕn ®æi Z cña sai ph©n tiÕn
Δf(k) = f(k+1) - f(k)
Z[Δf(k)]=(1-z-1)F(z) (3.13)
5. BiÕn ®æi Z cña sai ph©n lïi
Δf(k) = f(k) - f(k-1)
Z[Δf(k)]=(z - 1)F(z) (3.14)
6. Gi¸ trÞ ®Çu cña hµm gèc rêi r¹c f(0)
→∞
=z
f(0) lim F(z) (3.15)
H×nh 4.2- C¸c d¹ng tÝn hiÖu.
(a) Liªn tôc, (b) Gi¸n ®o¹n
x
(
t
)
0 t
(a) T kT
t
(b)
x
(
k
)
0
0
mm t
H
×nh 4.3- D¹ng tÝn hiÖu sau phÐp dÞch
Gi¸o tr×nh M« h×nh ho¸
Bé m«n Tù ®éng ho¸ http://www.ebook.edu.vn Khoa §iÖn
25
7. Gi¸ trÞ cuèi cña hµm gèc rêi r¹c f(0)
→
∞= −
z1
f( ) lim(z 1)F(z) (3.16)
3.5- Hµm truyÒn sè cña hÖ gi¸n ®o¹n
Hµm truyÒn sè cña hÖ gi¸n ®o¹n tuyÕn tÝnh lµ tû sè
gi÷a biÕn ®æi Z cña d·y tÝn hiÖu gi¸n ®o¹n ë ®Çu ra víi
biÕn ®æi Z cña d·y tÝn hiÖu gi¸n ®o¹n ë ®Çu vµo víi ®iÒu
kiÖn ®Çu b»ng kh«ng.
Gi¶ sö mét hÖ gi¸n ®o¹n ®−îc m« t¶ b»ng ph−¬ng
tr×nh sai ph©n tuyÕn tÝnh sau:
any(k+n)+...+aoy(k)=bmx(k+m)+...+box(k) (3.17)
trong ®ã m ≤ n, ®iÒu kiÖn nµy b¶o ®¶m kh¶ n¨ng
gi¶i ph−¬ng tr×nh (3.17) trªn m¸y tÝnh.
Thùc hiÖn biÕn ®æi Z c¸c phÇn tö cña ph−¬ng tr×nh
(3.16) víi ®iÒu kiÖn ®Çu b»ng 0 vµ tÝnh chÊt dÞch hµm gèc
®i n vµ m b−íc nh− ®· nªu ë ph−¬ng tr×nh (3.11) ta cã
hµm truyÒn sè sau:
mm1
mm1 o
nn1
nn1 o
b z b z ... b
Y(z)
W(z) X(z) a z a z ... a
−
−
−
−
+++
==+++
(3.18)
NÕu tÝn hiÖu vµo x(k) lµ xung ®¬n vÞ → hµm Dirac
δ th× ta cã: X(Z) = Z[δ(k)] = 1
Lóc nµy W(Z) = Y(Z) (3.19)
Nh− vËy còng gièng nh− trong tr−êng hîp biÕn ®æi Laplace, hµm truyÒn W(s) cña hÖ
liªn tôc lµ ph¶n øng cña hÖ ®èi víi hµm ®¬n vÞ 1(t), hµm truyÒn sè W(z) lµ ph¶n øng cña hÖ
thèng gi¸n ®o¹n ®èi víi tÝn hiÖu vµo lµ xung Dirac δ(k).
3.6- Hµm truyÒn sè cña hÖ liªn tôc
§èi víi hÖ liªn tôc ng−êi ta dïng biÕn ®æi Laplace gi¸n ®o¹n ®Ó t×m hµm truyÒn sè cña
hÖ liªn tôc, nh−ng phÐp biÕn ®æi nµy th−êng dÉn ®Õn hµm siªu viÖt ®èi víi biÕn s, do ®ã rÊt
khã tÝnh to¸n nªn kh«ng ®−îc dïng trong thùc tÕ. Trong thùc tÕ ng−êi ta dïng ph−¬ng ph¸p
chuyÓn ®æi tõ hµm truyÒn Lapace W(s) sang hµm truyÒn sè qua phÐp biÕn ®æi Z lµ W(z) b»ng
c¸ch thay biÕn sè:
z = esT (3.20)
Tõ biÓu thøc (3.20) ta cã thÓ gi¶i ®−îc:
1
slnz
T
= (3.21)
trong ®ã lnz cã thÓ khai triÓn thµnh chuçi:
35 k
k1
UU U
ln z 2(U ...) 2
35 k
∞
=
= +++=
∑
(3.22)
Trong ®ã:
1
1
1z z1
U1z z1
−
−
−−
==
++
B¶ng 4.1- nh Laplace vµ ¶nh Z
cña c¸c hµm th«ng dông
Hµm gèc F(s) F(z)
δ(t) 1 1
1(t) 1
s
z
z1
t 2
1
s −2
Tz
(z 1)
t2
3
2!
s
+
−
2
3
Tz(z 1)
(z 1)
t3
4
3!
s
+
+
−
32
4
Tz(z 4z 1)
(z 1)
e-et
+
1
sa
−
−aT
z
ze
te-et
+2
1
(s a) −
−
−
aT
aT 2
Tze
(z e )
Sin(ωt) ω
+ω
22
s
ω
−ω+
2
zsin( T)
z2zcos(T)1
Cos(ωt) +ω
22
s
s −ω
−ω+
2
2
zzcos(T)
z2zcos(T)1