Sưu tầm bởi:
www.daihoc.com.vn
Nguyến Tất Thu 0918927276 or 01699257507 http://www.toanthpt.net
Trường THPT Lê Hồng Phong – Biên Hòa – ðồng Nai
1
Trong các phần trước chúng ta ñã ñi xét một số dạng hệ mà có ñường lối giải tổng quát.
Trong phần này chúng ta ñi xét một số hệ mà không có ñường lối giải tổng quát. ðể tìm
lời giải của những hệ này
1. Phương pháp thế:
Nội dung của phương pháp này từ một phương trình hoặc kết hợp hai phương trình của
hệ ta biểu diễn ẩn này qua ẩn kia hoặc một biểu thức này qua biểu thức khác và thế vào
phương trình còn lại chuyển về phương trình một ẩn (có thể là ẩn phụ). Mục ñích của
việc làm này là giảm số ẩn. Tùy thuộc vào ñặc ñiểm của bài toán mà ta có những cách
biến ñổi phù hợp. Trong phương pháp này ta cần lưu ý một số dấu hiệu sau.
• Nếu trong hệ phương trình có một phương trình bậc nhất ñối với một ẩn thì ta rút ẩn
ñó qua ẩn kia thế vào phương trình còn lại và chuyển về giải phương trình một ẩn.
• Với hai số thực bất kì
x 0;y
≠
ta luôn có
y tx
(t là số
th
ự
c c
ầ
n tìm). V
ớ
i cách làm
này ta s
ẽ
ñượ
c h
ệ
v
ề
ph
ươ
ng trình m
ộ
t
ẩ
n t.
•
Ph
ươ
ng trình
f(x;y) f(y;x)
=
luôn có m
ộ
t c
ặ
p nghi
ệ
m
x y
=
(các b
ạ
n th
ử
gi
ả
i thích
vì sao?), do
ñ
ó ta luôn phân tích ph
ươ
ng trình
ñ
ã cho v
ề
d
ạ
ng:
(x y)g(x;y) 0
− =
.
•
Trong h
ệ
ph
ươ
ng trình n
ế
u bi
ể
u th
ứ
c
u(x)
xu
ấ
t hi
ệ
n
ở
hai ph
ươ
ng trình thì ta có th
ể
ñặ
t
t u(x)
=
ñể
làm
ñơ
n gi
ả
n hình th
ứ
c bài toán.
Ví dụ 1: Giải hệ phương trình:
3
x y 16 (1)
3x y 8 (2)
=
+ =
.
Giải :
Ta thấy (2) là một phương trình bậc nhất hai ẩn nên ta rút ẩn này qua ẩn kia.
Từ phương trình (2)
y 8 3x
⇒= −
thay vào phương trình (1) ta ñược:
3 4 3 2 2
x (8 3x) 16 3x 8x 16 0 (x 2) (3x 4x 4) 0 x 2
− = ⇔ − + = ⇔ − + + = ⇔ =
Vậy hệ có nghiệm là
x y 2
= =
.
Chú ý : Ở cách giải trên ta thấy hệ có nghiệm duy nhất
x y 2
= =
, ñồng thời từ hai
phương trình ta có nhận xét
x,y 0
>
và ở phương trình (2) VT là
3x y
+
, phương trình
(1) có tích
3
x y
. ðiều này gợi cho chúng ta liên tưởng ñến BðT Cauchy. Ta có cách
giải khác như sau:
Ta thấy nếu hệ có nghiệm (x;y) thì
x,y 0
>
.
Áp dụng bñt Cauchy ta có:
3
4
3x y x x x y 4 x y 8
+ = + + + ≥ =
.
ðẳ
ng th
ứ
c x
ả
y ra
x y 2
⇔ = =
. Th
ử
l
ạ
i ta th
ấ
y th
ỏ
a mãn.
Sưu tầm bởi:
www.daihoc.com.vn
Nguyến Tất Thu 0918927276 or 01699257507 http://www.toanthpt.net
Trường THPT Lê Hồng Phong – Biên Hòa – ðồng Nai
2
Ví dụ 2:
Gi
ả
i h
ệ
ph
ươ
ng trình:
(
)
2 2
2 2
y(1 x ) x 1 y (1)
x 3y 1 (2)
+ = +
+ =
.
Giải:
Dễ thấy phương trình (1) có cặp nghiệm
x y
=
, do ñó ta biến ñổi phương trình (1) của
hệ ra thừa số
(x y)
.
Ta có:
x y
(1) x y xy(y x) 0 (x y)(1 xy) 0
xy 1
=
⇔ − + − = ⇔ − − = ⇔
=
.
*
2
1
x y 4x 1 x
2
=⇒= ⇔ = ±
.
*
4 2
1
x 3y y 1 0
y
=⇒− + =
phương trình vô nghiệm.
Vậy nghiệm của hệ là:
1
x y
2
= = ±
.
Ví dụ 3: Giải hệ phương trình:
3
1 1
x y (1)
x y
2y x 1 (2)
− = −
= +
.
Giải:
xy 0
≠
Ta có
x y
x y 1
(1) x y 0 (x y)(1 ) 0
1
xy xy y
x
=
−
⇔ − + = ⇔ − + = ⇔
= −
.
*
x y
=
thay vào (2), ta ñược:
3 2
1 5
x 2x 1 0 (x 1)(x x 1) 0 x 1;x
2
− ±
− + = ⇔ − + − = ⇔ = = .
*
1
y
x
= −
thay vào (2), ta ñược:
4 2 2
1 1 3
x x 2 0 (x ) (x ) 0
2 2 2
+ + = ⇔ − + + + =
vô
nghiệm.
Vậy hệ ñã cho có ba cặp nghiệm:
1 5
x y 1;x y
2
− ±
= = = =
.
Sưu tầm bởi:
www.daihoc.com.vn
Nguyến Tất Thu 0918927276 or 01699257507 http://www.toanthpt.net
Trường THPT Lê Hồng Phong – Biên Hòa – ðồng Nai
3
Ví dụ 4: Giải các hệ phương trình sau:
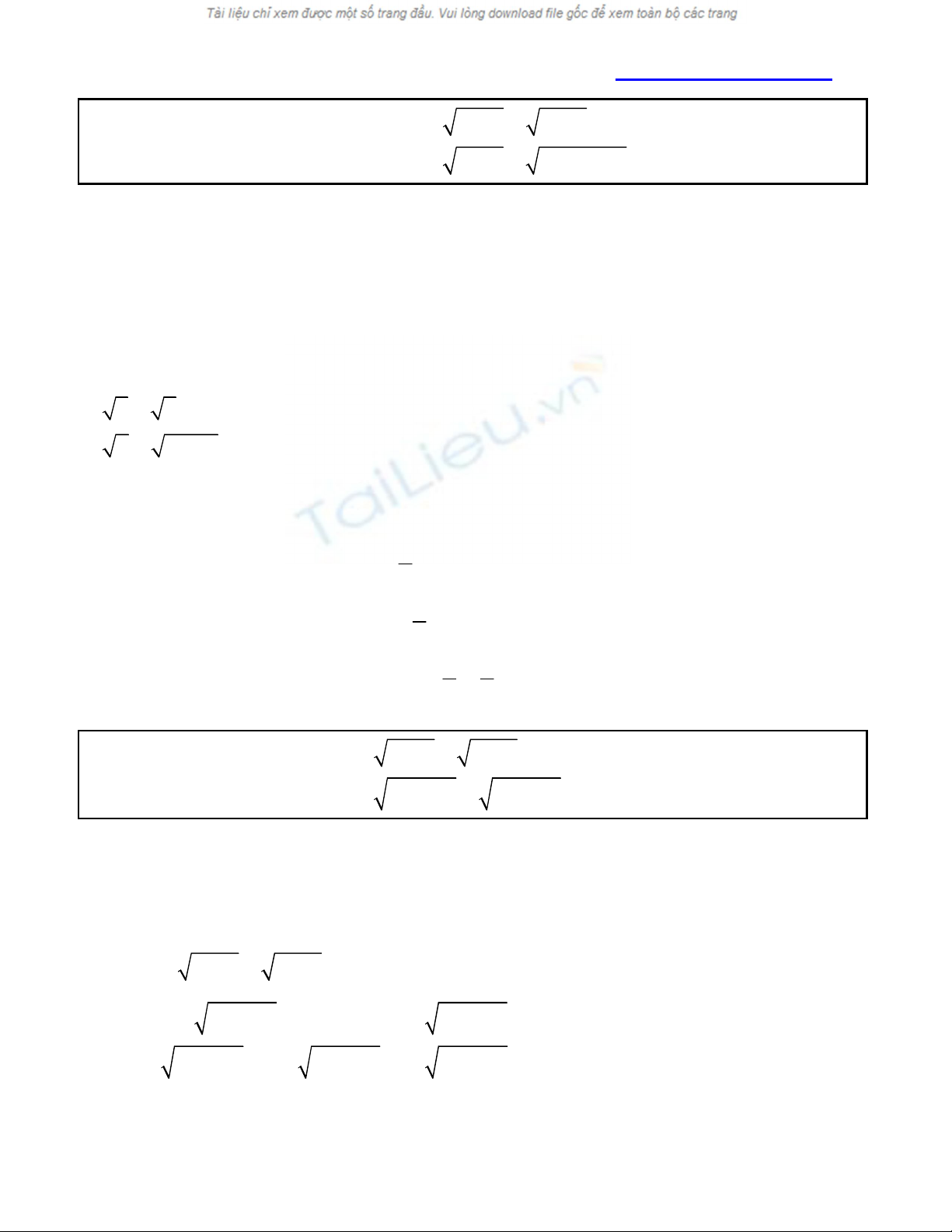
3
3
x y x y
x y x y 12
+ = +
− = − −
.
Giải: ðK:
x y 0
x y 0
+ ≥
− ≥
.
Ta thấy mỗi phương trình của hệ là phương trình một ẩn
x y
+
và
x y
−
. Do ñó ñiều
mà chúng ta nghĩ tới là ñi giải từng phương trình tìm
x y
+
và
x y
−
, khi ñó ta có ñược
hệ phương trình mới ñơn giản hơn nhiều.
ðể ñơn giản về mặt hình thức ta ñặt
a x y, b x y a,b 0
= + = − ⇒≥
ta có hệ :
3 2
3
3 2
3
a a a a a 0 V a 1
b 4
b b 12 b (b 12)
= = = =
⇔ ⇔
=
= − = −
.
*Với
a 0 x y 0 x 2
b 4 x y 4 y 2
= + = =
⇔ ⇔
= − = = −
* Với
5
x
a 1 x y 1
2
b 4 x y 4 3
y
2
=
= + =
⇔ ⇔
= − =
= −
Vậy nghiệm của hệ là:
5 3
(x;y) (2; 2), ( ; )
2 2
= − −
.
Ví dụ 4: Giải hệ phương trình:
2 2 2 2
x y x y 2 (1)
x y x y 4 (2)
+ − − =
+ + − =
.
Giải: ðK :
x | y |
≥
Vì (1) trong căn chỉ chứa lũy thừa bậc 1 ñối với x,y còn (2) thì trong căn chứa lũy thừa
bậc 2 ñối với x,y nên suy nghĩ ñầu tiên là ta sẽ bình phương hai vế phương trình (1) ñể
ñưa về hai phương trình ñồng bậc.
Từ (1)
x y x y y 0
⇒+ > − ⇒>
.
Hệ
2 2 2 2
2 2 2
2 2 2 2 2 2
2 2 2
2 x 6
x x y 2 x y x 2
x y (2 x)
x y 4 x y x y 6 x
x y (6 x)
≤ ≤
− − = − = −
⇔ ⇔ ⇔ − = −
+ = − − + = −
+ = −
Sưu tầm bởi:
www.daihoc.com.vn
Nguyến Tất Thu 0918927276 or 01699257507 http://www.toanthpt.net
Trường THPT Lê Hồng Phong – Biên Hòa – ðồng Nai
4
2 2 2 2 2
2 2 2 2
2 x 6 2 x 6
5
x
2
2x (2 x) (6 x) 2x 40 16x 2x
y 6
x y (6 x) y 36 12x
≤ ≤ ≤ ≤
=
⇔ = − + − ⇔ = − + ⇔
=
+ = − = −
.
Vậy nghiệm của hệ ñã cho là:
5
( ; 6)
2
.
Ví dụ 6: Giải hệ phương trình:
2
2
x 1 y(y x) 4y (1)
(x 1)(y x 2) y (2)
+ + + =
+ + − =
.
Giải:
ðặt
a x y
= +
từ (1)
2
x 1 y(4 a)
⇒+ = −
thế vào (2), ta có:
2
y(4 a)(a 2) y y(a 6a 9) 0 y 0; a 3
− − = ⇔ − + = ⇔ = =
* Với
y 0
=
thay vào (1) ta thấy hệ vô nghiệm.
* Với
a 3 x y 3
= ⇔ + =
thay vào hệ ta có:
2 2
x 1 y 2
x 1 y 3 x x x 2 0
x 2 y 5
=⇒=
+ = = − ⇔ + − = ⇔
= − ⇒=
.
Vậy hệ ñã cho có hai cặp nghiệm:
(x;y) (1;2), ( 2;5)
= −
.
Ví dụ 7: Giải hệ phương trình:
3 3
2 2
x 8x y 2y (1)
x 3 3(y 1) (2)
− = +
− = +
.
Giải:
Cách 1: Từ (2)
2 2
x 3(y 2)
⇒= +
(3) thay vào (1) ta ñược :
2
3 2 2 2
x 0
x
x 8x y(y 2) y x(3x xy 24) 0
3x 24
3y
x
=
− = + = ⇔ − − = ⇔
−
=
.
* Với
x 0
=
thay vào (3) ta có:
2
y 2 0
+ =
vô nghiệm.
* Với
2
3x 24
y
x
−
= thay vào (3) ta ñược:
2
2
2
3x 24
x 3 6
x
−
= +
2
4 2 2
x 3 y 1
x 9
13x 213x 864 0
96 78
96 x y
x
13 13
13
= ±
⇒
= ±
=
⇔ − + = ⇔ ⇔
= ±
⇒
=
=
∓
.
Sưu tầm bởi:
www.daihoc.com.vn
Nguyến Tất Thu 0918927276 or 01699257507 http://www.toanthpt.net
Trường THPT Lê Hồng Phong – Biên Hòa – ðồng Nai
5
Vậy hệ có bốn cặp nghiệm:
96 78
(x;y) ( 3; 1), ( ; )
14 13
= ± ± ±
∓
.
Cách 2: Ta thấy
x 0
=
không là nghiệm của hệ nên ta ñặt
y tx
. Khi ñ
ó h
ệ
tr
ở
thành
3 3 3 2 3 3
2
2 2 2 2 2
x 8x t x 2tx x (1 t ) 2t 8
1 t t 4
3
1 3t
x 3 3(t x 1) x (1 3t ) 6
− = + − = +
− +
⇔
⇒
=
−
− = + − =
3 2 2
1
t
3
3(1 t ) (t 4)(1 3t ) 12t t 1 0
1
t
4
=
⇔ − = + − ⇔ − − = ⇔
= −
.
*
2 2
x (1 3t ) 6
x 3
1
tx
y 1
3y3
− =
= ±
=
⇒
⇔
= ±
=
.
*
4 78
x
1
13
t4
78
y
13
= ±
= −
⇒
=
∓
.
Ví dụ 8:
Gi
ả
i h
ệ
ph
ươ
ng trình:
2
2
| x 2x | y 1 (1)
x | y| 1 (2)
− + =
+ =
.
Giải: Từ (2)
1 x,y 1
⇒− ≤ ≤
.
Ta xét các trường hợp sau
*
y 0
≥
2 2
(1) x y 1 y 1 x
⇒⇔ + = ⇔ = −
thay vào (2) ta ñược:
2 2 2 2 2 2 4 2
| x 2x | 1 x 1 | x 2x | x x (x 2) x x ( 4x 4) 0
− + − = ⇔ − = ⇔ − = ⇔ − + =
x 0 y 1
x 1 y 0
=⇒=
⇔
=⇒=
*
2
y 0 (1) y x 1
<⇒⇔ = −
thay vào (2) ta có:
2 2 2 2 3 2 2
| x 2x | x 1 1 | x 2x | 2 x x 2x 1 0 (x 1)(x x 1) 0
− + − = ⇔ − = − ⇔ − + = ⇔ − − − =
x 1
1 5 1 5
x y
2 2
=
⇔− −
=⇒=
.