
1
Mã số
- Tên sáng kiến: “Một số giải pháp nâng cao hiệu quả giảng dạy loại bài tập
về số chính phương cho học sinh giỏi lớp 8 ở trường trung học cơ sở”.
- Lĩnh vực áp dụng: Lĩnh vực tự nhiên
- Họ tên tác giả: Nguyễn Thị Thanh Nga
- Đơn vị công tác: Trường TH & THCS Tân Phong
Tân phong, tháng 01/2019

2
- Tên sáng kiến:Một số giải pháp nâng cao hiệu quả giảng dạy loại bài tập
về số chính phương cho học sinh giỏi lớp 8 ở trường trung học cơ sở
-Mô tả bản chất sáng kiến
+ Nội dung sáng kiến
Thực trạng
Trong quá trình dạy học, đặc biệt trong quá trình bồi dưỡng học sinh giỏi,
bản thân tôi nhận thấy khả năng tiếp thu và vận dụng kiến thức của học sinh về số
chính phương vẫn còn nhiều lúng túng, không định hướng được cách giải cho nên
trong học tập hay thi cử khi gặp các bài toán về số chính phương các em thường
mong chờ may rủi. Nếu các em được giáo viên hướng dẫn có hệ thống thì các em
hoàn toàn có thể chủ động giải được loại bài toán này, từ đó phát huy được tố chất
toán học tiềm ẩn trong học sinh, chấm dứt sự mong chờ may rủi trong kiểm tra thi
cử của học sinh, đáp ứng nhu cầu đổi mới phương pháp dạy học hiện nay.
Các giải pháp thực hiện
* Giải pháp 1: Hệ thống các kiến thức cơ bản về số chính phương.
+ Định nghía số chính phương
Số chính phương là số bằng bình phương của một số tự nhiên.
Mười số chính phương đầu tiên là: 0, 1, 4, 9, 16, 25, 36, 49, 64, 81.
+ Một số tính chất của số chính phương.
1- Số chính phương chỉ có thể có chữ số tận cùng bằng 0, 1, 4, 5, 6, 9; không thể có
chữ tận cùng bằng 2, 3, 7, 8.
2- Khi phân tích một số chính phương ra thừa số nguyên tố, ta được các thừa số là
lũy thừa của số nguyên tố số mũ chẵn.
3- Số chính phương chỉ có thể có một trong hai dạng 4n hoặc 4n+1. Không có số
chính phương nào có dạng 4n + 2 hoặc 4n + 3 (n
N).
4- Số chính phương chỉ có thể có một trong hai dạng 3n hoặc 3n +1. Không có số
chính phương nào có dạng 3n + 2 ( n
N ).
5- Số chính phương tận cùng bằng 1, 4 hoặc 9 thì chữ số hàng chục là chữ số chẵn.
Số chính phương tận cùng bằng 5 thì chữ số hàng chục là 2.
Số chính phương tận cùng bằng 6 thì chữ số hàng chục là chữ số lẻ.
6- Số chính phương chia hết cho 2 thì chia hết cho 4.
Số chính phương chia hết cho 3 thì chia hết cho 9
Số chính phương chia hết cho 5 thì chia hết cho 25
Số chính phương chia hết cho 8 thì chia hết cho 16.
7- Giữa hai số chính phương liên tiếp không có số chính phương nào.

3
8- Nếu hai số nguyên liên tiếp có tích là một số chính phương thì một trong hai số
nguyên đó là số 0.
* Giải pháp 2: Phân loại các dạng bài tập.
1. Loại bài tập “Nhận dạng xem một số có là số chính phương không”
2. Loại bài tập “Chứng minh một số là số chính phương”.
3. Loại bài tập “Chứng minh một số không là số chính phương”.
4. Loại bài tập “Tìm số chính phương”.
5. Loại bài tập “Tìm giá trị của biến để biểu thức là số chính phương”.
* Giải pháp 3: Hướng dẫn cách giải đối với mỗi loại bài tập, đưa ra ví dụ cụ
thể và lời giải chi tiết.
1. Loại bài tập “Nhận dạng xem một số có là số chính phương không”
Trong dạng bài tập này nếu theo định nghĩa về số chính phương thì các số trong các
bài tập đề cập đến quá nhiều chữ số, rất khó phát hiện nó là bình phương của số nào
ngay cả khi sử dụng máy tính cầm tay vì số chữ số của mỗi số tràn màn hình. Nếu
giáo viên không phát hiện ra tính chất của số chính phương thì sẽ không thể giải
được bài tập loại này. Do đó để giải được loại bài tập này tôi đã hướng dẫn học
sinh phát hiện và nên sử dụng tính chất nào của số chính phương thì mới giải được.
Ví dụ 1: Hãy xét xem các số sau có phải là số chính phương không?
M = 1345678910111213
N = 1234567891011121314151617
P = 1234567891011121314151617181920212223
Giáo viên hướng dẫn: Để xét xem các số cụ thể trên có là số chính phương
không, ta sử dụng tính chất của số chính phương đó là “số chính phương không tận
cùng bởi các chữ số 2; 3; 7; 8”
Giải
Trước tiên ta xét chữ số tận cùng của các số M, N, P
M = 1345678910111213 có chữ số tận cùng là 3
N = 1234567891011121314151617 có chữ số tận cùng là 7
P = 1234567891011121314151617181920212223 có chữ số tận cùng là 3
Vậy M, N, P đều không phải là số chính phương.
Ví dụ 2: Các số sau có là số chính phương không?
2 2 2
1992 1993 1994
A
2 2 2 2
1992 1993 1994 1995
B
100 100 100
1 9 94 1994
P
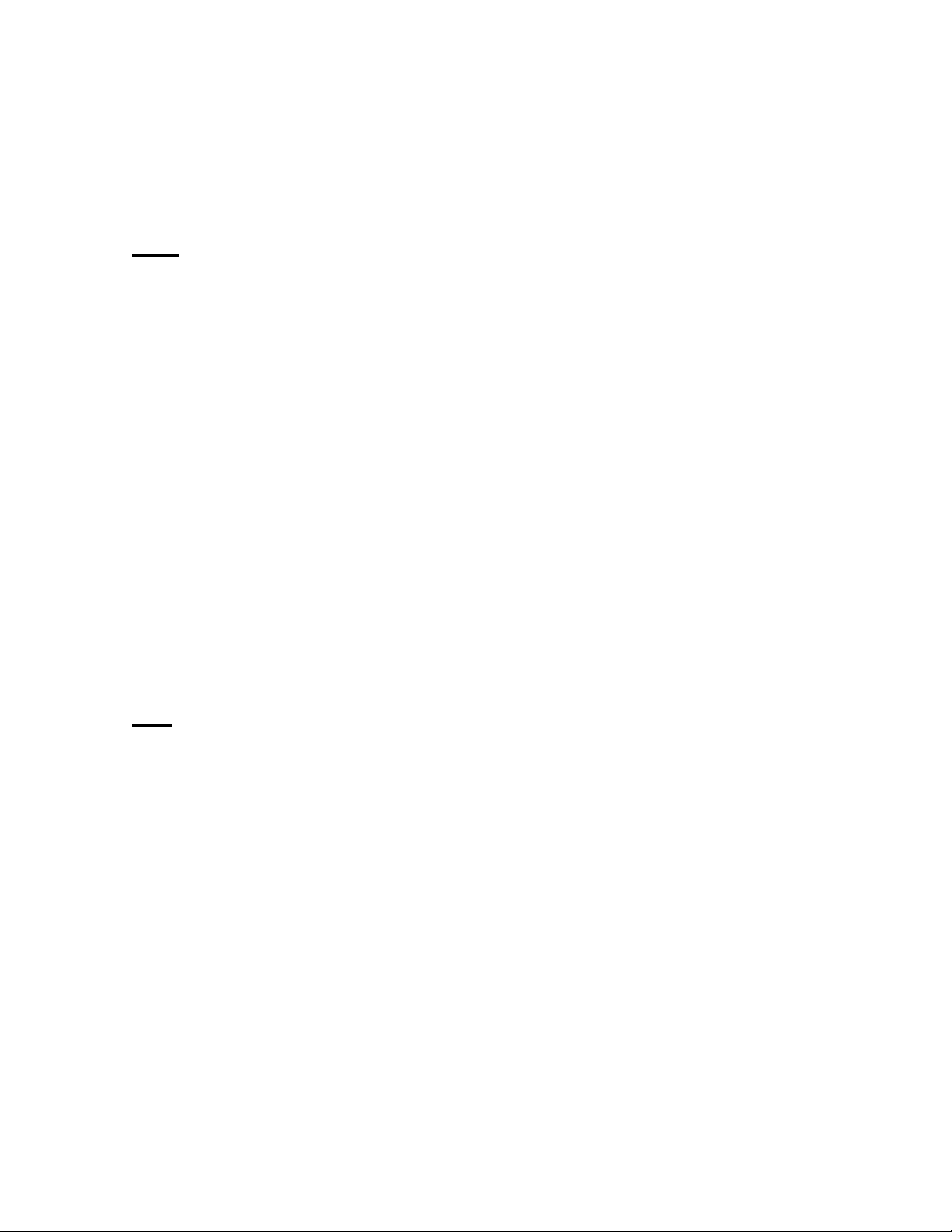
4
Giáo viên hướng dẫn: Áp dụng tính chất 3- Số chính phương chỉ có thể có
một trong hai dạng 4n hoặc 4n+1. Không có số chính phương nào có dạng 4n + 2
hoặc 4n + 3 (n
N).
Và tính chất 4- Số chính phương chỉ có thể có một trong hai dạng 3n hoặc 3n +1.
Không có số chính phương nào có dạng 3n + 2 ( n
N ).
Giải:
Các số
3 2
1993 ,1994
là số chính phương không chia hết cho 3 nên chia cho 3
dư 1, còn
2
1992
chia hết cho 3. Số A là số chia cho 3 dư 2, không là số chính
phương.
Các số
2 2
1992 ,1994
là số chính phương chẵn nên chia hết cho 4.Các số
2 2
1993 ,1995
là số chính phương lẻ nên chia cho 4 dư 1. Số B là số chia cho 4 dư 2, không là số
chính phương.
Các số
100 100
94 ,1994
là số chính phương chẵn nên chia hết cho 4. Còn
100
9
là
số chính phương lẻ nên chia cho 4 dư 1.Số P là số chia cho 4 dư 2, không là số
chính phương.
Ví dụ 3: Trong dãy sau có tồn tại số nào là số chính phương không?
11, 111, 1111, 11111, ...
Giáo viên hướng dẫn: Áp dụng tính chất3- Số chính phương chỉ có thể có
một trong hai dạng 4n hoặc 4n+1. Không có số chính phương nào có dạng 4n + 2
hoặc 4n + 3 (n
N).
Giải
Mọi số của dãy đều tận cùng bởi 11 nên là số chia cho 4 dư 3. Mặt khác, số chính
phương lẻ thì chia cho 4 dư 1.
Vậy không có số nào của dãy là số chính phương
2. Loại bài tập “Chứng minh một số là số chính phương”.
Với dạng bài tập này các số mà bài tập đề cập thường rất phức tạp không đơn
giản để phát hiện nó là bình phương của một số. Do vậy với từng số, từng biểu thức
cần biến đổi để đưa chúng về các hằng đẳng thức bình phương của một tổng hoặc
bình phương của một hiệu. Cách biến đổi như thế nào cho hiệu quả nhất thì tôi đã
hướng dẫn cụ thể trong các ví dụ. Sau đây là các ví dụ minh họa mà tôi đã áp dụng.
Ví dụ 1: Chứng minh rằng các số sau đây là số chính phương
a) A = 11 … 1
ố
-22… 2
ố
b) B = 224 99…9
ố 1 00… 0
9
ố

5
c) C =44 … 4
ố 88 … 8
ố 9
Giáo viên hướng dẫn: Khi biến đổi một số trong đó có nhiều chữ số giống nhau
thành một số chính phương tức là biến đổi chúng về bình phương của một tổng
hoặc một hiệu ta nên đặt11 … 1
=a và như vậy: 99 … 9
+ 1 = 10 = 9a +1
Giải
a, A = 11 …1
ố
-22 … 2
ố
= 11 …1
ố 00 …0
ố
+11 … 1
ố
- 2.11 …1
ố
= 11 … 1
ố
.10 - 11 …1
ố
Đặt 11 … 1
=a
99 …9
ố
= 9a
9a +1 = 10
Do đó A = a(9a + 1) – a =
2
2
9 3
a a
= (33 …3
ố
)2 là một số chính phương.
b, B = 224 99 … 9
ố 1 00 …0
9
ố
= 224.10 + 99 … 9
ố
10 +10 +9
= 224.10 + (10 − 1)10 + 10 +9
= 224.10 + 10 - 10 +10 +9
= 225.10 - 9. 10+ 9
= 225.10 - 90. 10+ 9
=
2
1510 3
n
Vậy B là một số chính phương
c, C =44 … 4
ố 88 … 8
ố 9
= 4.11 …1
ố
.10 + 8.11 … 1
ố
+ 1
= 4.
1
10 1
9
n
.10 +8.
1
10 1
9
n
+ 1
= 2 2 1
4.10 4.10 1
9
n n
=
2
1
2.10 1
3
n
Vì 1
2.10 1
n
luôn chia hết cho 3 nên C là một số chính phương.
Ví dụ 2: Cho S = 1.2.3 + 2.3.4 + 3.4.5 + ...+ k(k + 1)(k + 2) (k
N).
Chứng minh rằng 4S + 1 là số chính phương.
Giáo viên hướng dẫn:Tính tổng S là một dãy có quy luật:


























