
A. ĐT V N Đ:Ặ Ấ Ề
Hi n nay, s nghi p giáo d c và đào t o đang đi m i tr c yêuệ ự ệ ụ ạ ổ ớ ướ
c u phát tri n kinh t - xã h i theo h ng công nghi p hoá và hi n điầ ể ế ộ ướ ệ ệ ạ
hoá c a đt n c. Đó là đào t o con ng i năng đng, sáng t o, chủ ấ ướ ạ ườ ộ ạ ủ
đng trong h c t p, thích nghi t t v i cu c s ng và lao đng. Vì th ,ộ ọ ậ ố ớ ộ ố ộ ế
ng i giáo viên bên c nh vi c d y cho h c sinh n m v ng các n iườ ạ ệ ạ ọ ắ ữ ộ
dung c b n v ki n th c, còn ph i d y cho h c sinh bi t suy nghĩ, tơ ả ề ế ứ ả ạ ọ ế ư
duy sáng t o, t o cho h c sinh có nhu c u nh n th c trong quá trìnhạ ạ ọ ầ ậ ứ
h c t p.ọ ậ
Trong t t cá các môn h c c p THCS, toán h c nói chung và hìnhấ ọ ấ ọ
h c nói riêng thì hình h c là m t phân môn r t quan tr ng trong vi cọ ọ ộ ấ ọ ệ
rèn luy n tính lôgic, t duy sáng t o, giúp h c sinh không nh ng h cệ ư ạ ọ ữ ọ
t t môn Toán mà còn có th h c t t các môn h c khác. Vi c khai thác,ố ể ọ ố ọ ệ
phát tri n m t bài toán đn gi n góp ph n r t quan tr ng trong vi cể ộ ơ ả ầ ấ ọ ệ
nâng cao năng l c t duy cho h c sinh. Qua nhi u năm gi ng d y, b nự ư ọ ề ả ạ ả
thân tôi nh n th y:ậ ấ
Các giáo viên gi ng d y toán đu đánh giá cao t m quan tr ng c aả ạ ề ầ ọ ủ
vi c khai thác, phát tri n t m t bài toán mà h c sinh đã gi i đc.ệ ể ừ ộ ọ ả ượ
Vi c khai thác gi thi t, khai thác sâu thêm k t qu c a bài toán đ t oệ ả ế ế ả ủ ể ạ
ra các bài toán khác (đn gi n ho c ph c t p h n)ơ ả ặ ứ ạ ơ là r t quan tr ng vàấ ọ
có ích. Nó không ch giúp ng i d y và ng i h c n m b t kĩ ki nỉ ườ ạ ườ ọ ắ ắ ế
th c c a m t d ng toán mà nó còn nâng cao tính khái quát hoá, đc bi tứ ủ ộ ạ ặ ệ
hoá, t ng quát hoá m t bài toán; t đó phát tri n t duy, nâng cao tínhổ ộ ừ ể ư
sáng t o, linh ho t cho các em h c sinh; giúp cho h c sinh n m ch c,ạ ạ ọ ọ ắ ắ
hi u sâu r ng ki n th c h n m t cách lôgic, khoa h c; t o h ng thúể ộ ế ứ ơ ộ ọ ạ ứ
yêu thích b môn toán h n. Nh ng h u h t h c sinh ( k c h c sinhộ ơ ư ầ ế ọ ể ả ọ
khá gi i) sau khi gi i xong m t bài toán đu thoã mãn v i nó mà khôngỏ ả ộ ề ớ
có ý th c khai thác, phát tri n nó thành chùm bài toán liên quan nhau.ứ ể
Chính đi u này làm h n ch s phát tri n t duy, tính sáng t o và linhề ạ ế ự ể ư ạ
ho t c a h c sinh. ạ ủ ọ
Chúng ta bi t r ng, m i m t bài toán đu có gi thi t và k t lu nế ằ ỗ ộ ề ả ế ế ậ
c a nó. Vi c ch ng minh k t lu n đó là yêu c u b t bu c h c sinhủ ệ ứ ế ậ ầ ắ ộ ọ
ph i th c hi n. Song, chúng ta c n rèn cho h c sinh suy nghĩ đng sauả ự ệ ầ ọ ằ
bài t p đó còn có th khai thác đc gì, khai thác nh th nào đó m i làậ ể ượ ư ế ớ
v n đ c n thi t đ giúp h c sinh phát tri n t duy, tính sáng t o vàấ ề ầ ế ể ọ ể ư ạ
linh ho t. Ch ng h n: Chúng ta khai thác thêm đc bài toán m i nàoạ ẳ ạ ượ ớ
t bài toán đó, thay đi m t s gi thi t thì cho ra bài toán m i nào, hayừ ổ ộ ố ả ế ớ
nh đo ng c bài toán thì sao?...ư ả ượ
Trong ch ng trình hình h c 8, có nhi u bài toán hay và khó dànhươ ọ ề
cho h c sinh gi i nh ng l i xu t phát t bài toán đn gi n. Ch v i sọ ỏ ư ạ ấ ừ ơ ả ỉ ớ ự
thay đi m t vài gi thi t có th t o ra m t h bài t p hay và nó giúpổ ộ ả ế ể ạ ộ ệ ậ
cho h c sinh phát tri n t duy r t nhi u. Qua d y gi ng d y nhi u nămọ ể ư ấ ề ạ ả ạ ề
l p 8 tôi xin trao đi kinh nghi m: ớ ổ ệ “Khai thác và phát tri n t m tể ừ ộ
bài toán đn gi n đ b i d ng toán 8“.ơ ả ể ồ ưỡ
B. GI I QUY T V N Đ.Ả Ế Ấ Ề
Chúng ta b t đu b ng bài toán c b n sau:ắ ầ ằ ơ ả
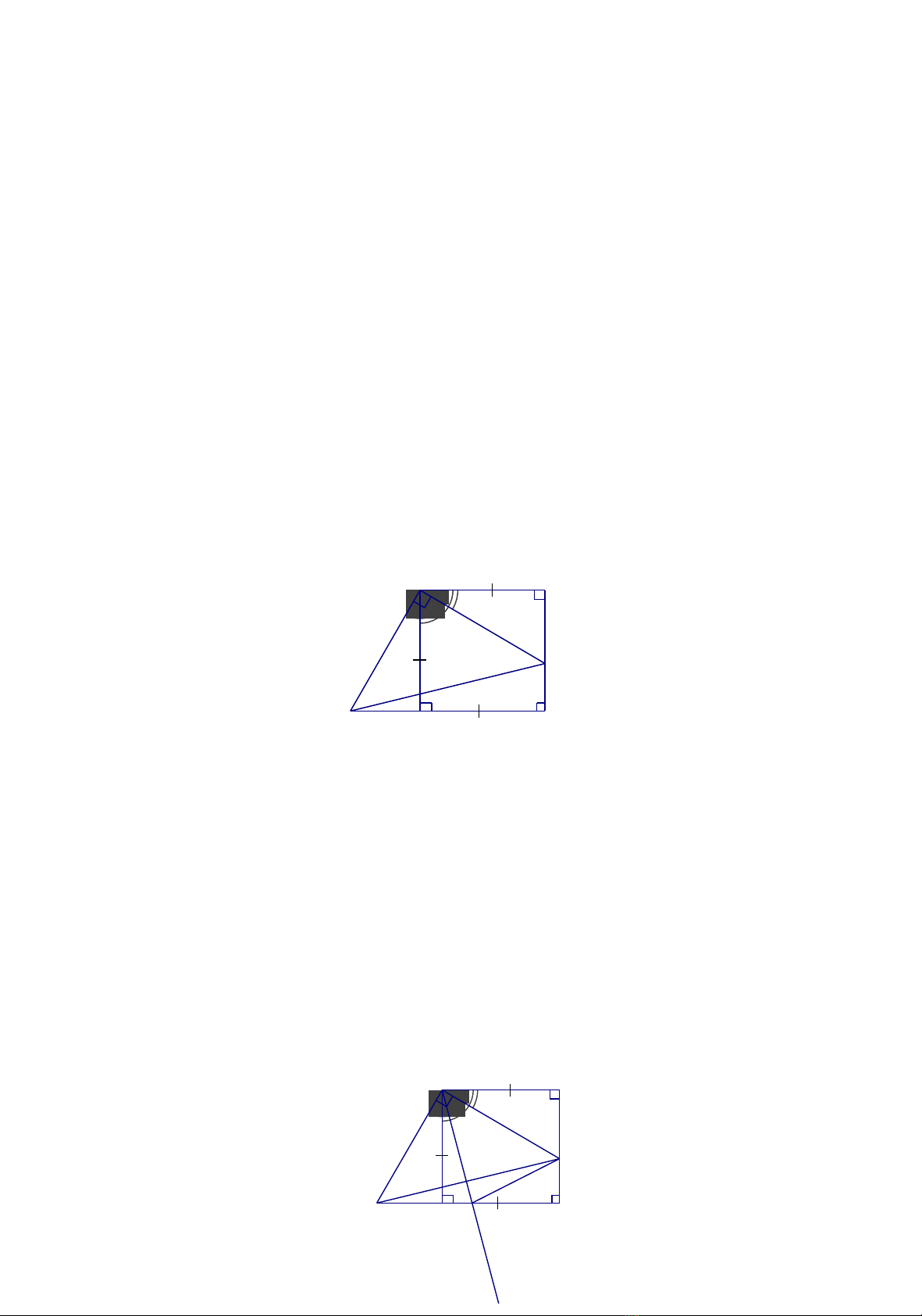
Bài toán 1 ( Bài toán c b n):ơ ả
Cho hình vuông ABCD. G i I là mọt đi m thay đi trên c nh AB.ộ ể ổ ạ
Đng th ng qua D vuông góc v i DI c t tia BC t i L. Ch ng minhườ ẳ ớ ắ ạ ứ
r ng: Tam giác DIL cân. ằ
H ng d n:ướ ẫ
ADI, CDL có:
AD=CD
= =90 ( tính ch t hình vuông)ấ
= ( cùng ph v i )ụ ớ
ADI = CDL ( c.g.c)
DI = DL.
V y : ậDIL cân t i D. ạ
Khai thác bài toán: T bài toán 1, n u ta k đng phân giác c từ ế ẻ ườ ắ
c nh BC t i M. ạ ạ
3
2
1
L
D
C
B
I
A
M
A
I
B
C
D
L
1
2
3
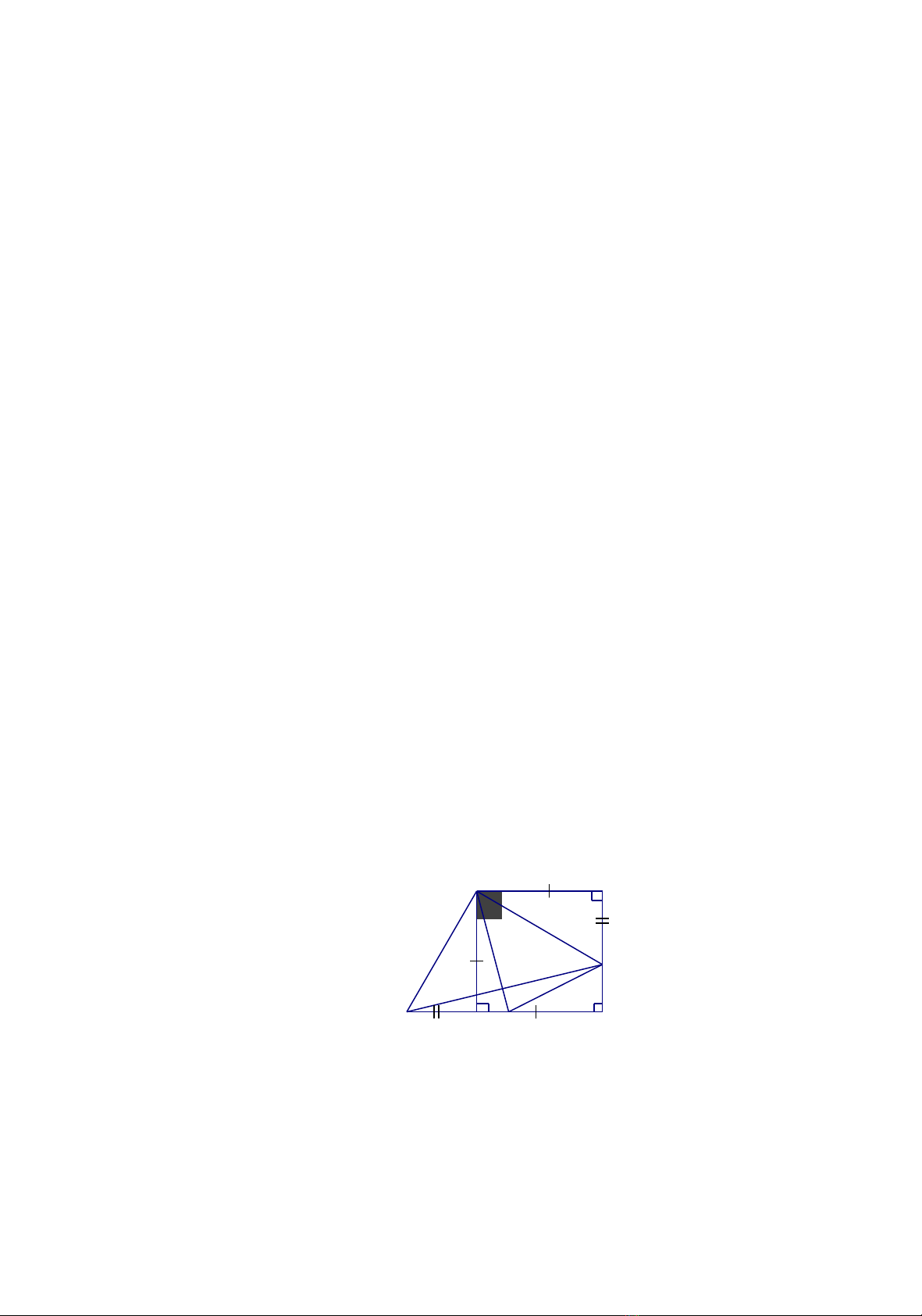
Khi đó: = 45
LDM = IDM
ML = MI
P = IB + BM + MI
= IB + BM + ML
= IB + BC + CL
= BC + BA = P ( V i P là chu vi )ớ
Do đó ta có bài toán 2 sau đây:
Bài toán 2:
Cho hình vuông ABCD. G i I là mọt đi m thay đi trên c nh AB.ộ ể ổ ạ
L y đi m M trên c nh BC sao cho = 45 . ấ ể ạ
Ch ng minh r ng: Chu vi ứ ằ IBM b ng m t n a chu vi hình vuôngằ ộ ữ
ABCD.
H ng d n:ướ ẫ
Nh v y t bài toán 1, ta c n ph i t o ra ư ậ ừ ầ ả ạ ADI = CDL ( c.g.c)
b ng cách v thêm đng ph nh sau:ằ ẽ ườ ụ ư
Trên tia đi c a tia CB, l y đi m L sao cho CL=AIố ủ ấ ể
CLD=AID (c.g.c)
DL=DI, = (1)
Mà + + = = 90 ( tính ch t hình vuông)ấ
3
2
4
45
°
1
L
D
C
B
I
A
M

+ = 90 - = 45 (2)
T 1,2 suy ra: + = 45 hay = 45 ừ
LDM = IDM (c.g.c)
ML = MI
Do đó: P = IB + BM + MI
= IB + BM + ML
= IB + BM + CL + CM
= IB + BM + AI + CM
= (BI + AI) + (BM + MC)
= AB + BC= P .
Đ d y cho h c sinh đi trà, ta có th chia bài toán thành nhi u ýể ạ ọ ạ ể ề
nh sau:ư
“Cho hình vuông ABCD. G i I là mọt đi m thay đi trên c nh AB.ộ ể ổ ạ
L y đi m M trên c nh BC sao cho = 45 . ấ ể ạ
a, Trên tia đi c a tia CB, l y đi m L sao cho CL=AI. Ch ng minhố ủ ấ ể ứ
r ng: ằ
CLD =
AID.
b, Ch ng minh r ng: ML = MI.ứ ằ
c, Ch ng minh r ng: Chu vi ứ ằ
IBM b ng m t n a chu vi hìnhằ ộ ữ
vuông ABCD.”
Khai thác bài toán: Đt câu h i ng c l i v i bài toán 2, n u chuặ ỏ ượ ạ ớ ế
vi IBM b ng m t n a chu vi hình vuông ABCD thì s đo = 45 hayằ ộ ữ ố
không?
Ta có ti p bài toán 3 sau đây:ế
Bài toán 3:
Cho hình vuông ABCD. G i I là mọt đi m thay đi trên c nh AB.ộ ể ổ ạ
L y đi m M trên c nh BC sao cho chu vi ấ ể ạ IBM b ng m t n a chu viằ ộ ữ
hình vuông ABCD. Ch ng minh r ng: = 45. ứ ằ
H ng d n:ướ ẫ
V n t bài toán 1, ta c n ph i t o ra ẫ ừ ầ ả ạ ADI = CDL ( c.g.c) b ngằ
cách v thêm đng ph nh sau:ẽ ườ ụ ư
Trên tia đi c a tia CB, l y đi m L sao cho CL=AIố ủ ấ ể
4
M
A
I
B
C
D
L
1
2
3

CLD=AID (c.g.c)
DL=DI, = (1)
Ta có:P = P
IB + BM + MI = AB + BC
IB + BM + MI = BI + AI + BM + MC
MI = AI + MC (2)
T 1,2 suy ra: MI = CL + MC = MLừ
LDM = IDM (c.c.c)
= hay + =
+ =
Mà + + = = 90 ( tính ch t hình vuông)ấ
= 45.
V y : = 45 ậ
Đ d y cho h c sinh đi trà, ta có th chia bài toán thành nhi u ýể ạ ọ ạ ể ề
nh sau:ư
“Cho hình vuông ABCD. G i I là mọt đi m thay đi trên c nh AB.ộ ể ổ ạ
L y đi m M trên c nh BC sao cho chu vi ấ ể ạ
IBM b ng m t n a chu viằ ộ ữ
hình vuông ABCD.
a, Trên tia đi c a tia CB, l y đi m L sao cho CL=AI. Ch ng minhố ủ ấ ể ứ
r ng: ằ
CLD=
AID.
b, Ch ng minh r ng: ứ ằ LDM = IDM
c, Ch ng minh r ng: = 45.” ứ ằ
Khai thác bài toán: Trong bài toán 3, chu vi IBM b ng m t n aằ ộ ữ
chu vi hình vuông ABCD. Nên chu vi IBM b ng 2a ( v i a là đ dàiằ ớ ộ
c nh hình vuông ABCD cho tr c) không đi nh ng di n tích ạ ướ ổ ư ệ IBM
thì luôn thay đi do đ dài c nh MI ph thu c vào v trí đi m di đng Iổ ộ ạ ụ ộ ị ể ộ
trên c nh AB kéo theo di n tích ạ ệ DMI cũng thay đi. Lúc này v n đổ ấ ề
đt ra là di n tích ặ ệ DMI l n nh t là bao nhiêu khi đi m I v trí nàoớ ấ ể ở ị
trên AB?


























