
XÂY DỰNG MỘT SỐ PHƯƠNG PHÁP GIẢI BÀI TOÁN BẤT
ĐẲNG THỨC ĐẠI SỐ KHI BỒI DƯỠNG HỌC SINH GIỎI LỚP 8
I. MỞ ĐẦU
1.1. Lý do chọn đề tài
Bài toán về bất đẳng thức là một nội dung quan trọng thường gặp trong
chuyên đề BDHSG phần đại số. Thông thường học sinh nắm chắc định
nghĩa và tính chất vận dụng làm tốt các bài tập về bất đẳng thức ở trong
sách giáo khoa Toán 8, tuy nhiên khi gặp những bài toán trong đề thi học
sinh giỏi Toán 8 thì rất khó khăn lúng túng không thể tìm ra phương pháp
giải cũng như cách trình bày lời giải bài toán bất đẳng thức Vì vậy, việc
tổng hợp, khái quát thành phương pháp giải đối với bài toán bất đẳng thức
là một chìa khoá giúp học sinh biến bài toán bất đẳng thức phức tạp thành
những bài toán đơn giản, có lối đi riêng một cách rõ ràng, từ đó dễ dàng vận
dụng vào giải các bài tập trong chuyên đề bất đẳng thức, nâng cao chất
lượng bồi dưỡng đội tuyển HSG môn Toán nói chung.
Với những lí do trên, tôi chọn đề tài "Xây dựng một số phương pháp
giải bài toán bất đẳng thức đại số khi bồi dưỡng học sinh giỏi lớp 8".”.
Đây là sự đúc rút kinh nghiệm nhằm cung cấp cho học sinh phương pháp ,
giúp học sinh tìm được hướng giải hợp lý nhất cho mỗi bài toán. Giúp học
sinh biết vận dụng định nghĩa, tính chất về bất đẳng thức và một số phương
pháp khác để giải bài toán bất đẳng .
1.2. Điểm mới của đề tài.
Đề tài bám sát chuẩn kiến thức kỹ năng, các phương pháp dạy học
phổ biến nhằm hình thành cho các em tư duy khoa học hơn.
Bài tập về bất đẳng thức rất đa dạng và phong phú. Để giải các bài tập loại
này chỉ dùng kiến thức về định nghĩa và tính chất thì chưa đủ. Muốn làm tốt
các bài tập về bất đẳng thức HS cần phải nắm vững các kiến thức sau:
1.1 - Sử dụng định nghĩa
1.2 - Sử dụng tính chất
1.3 - Các bất đẳng thức sẳn có xem như một hệ quả
1.4 - Đặt biến phụ
1.5 - Phương pháp làm trội
1.6 - Bất đẳng thức ba cạnh của một tam giác

1.7 - Phương pháp quy nạp.
Để thực hiện các nhiệm vụ nghiên cứu nêu ở trên, tôi thực hiện các giải pháp
sau :
+ Nghiên cứu lý thuyết: Tổng quan các tài liệu về lí luận dạy học, các văn
bản chỉ đạo về đổi mới, nâng cao chất lượng dạy học ở trường phổ thông,
các bài tập nâng cao, các bài tập chuyên chọn
+ Từ việc nghiên cứu lí thuyết lựa chọn các bài tập cơ bản, điển hình cho
mỗi dạng sau đó tổng hợp thành phương pháp giải cho mỗi dạng trong bài
toán bất đẳng thức
+ Nghiên cứu cơ sở lí luận về Bài tập bất đẳng thức ở trường phổ thông.
+ Nghiên cứu và khai thác một số bài tập cơ bản trong chuyên đề bồi
dưỡng HSG chuyên đề bất đẳng thức
+ Thiết kế và xây dựng các bài tập mẫu về toán bất đẳng thức trong
chương trình bồi dưỡng HSG môn Toán lớp 8
+ Nghiên cứu hiệu quả của việc áp dụng phương pháp giải bài toán bất
đẳng thức vào quá trình bồi dưỡng HSG môn Toán 8.
2. PHẦN NỘI DUNG
2.1. Thực trạng của vấn đề mà đề tài cần giải quyết
Trong năm học 2016-2017 và năm học 2017-2017 , sau khi đội tuyển
HSG của trường được chọn tham gia bồi dưỡng tại lớp “ Bồi dưỡng
HSG toán “ của PGD huyện Lệ Thủy, tôi đã thống kê về kết quả chất
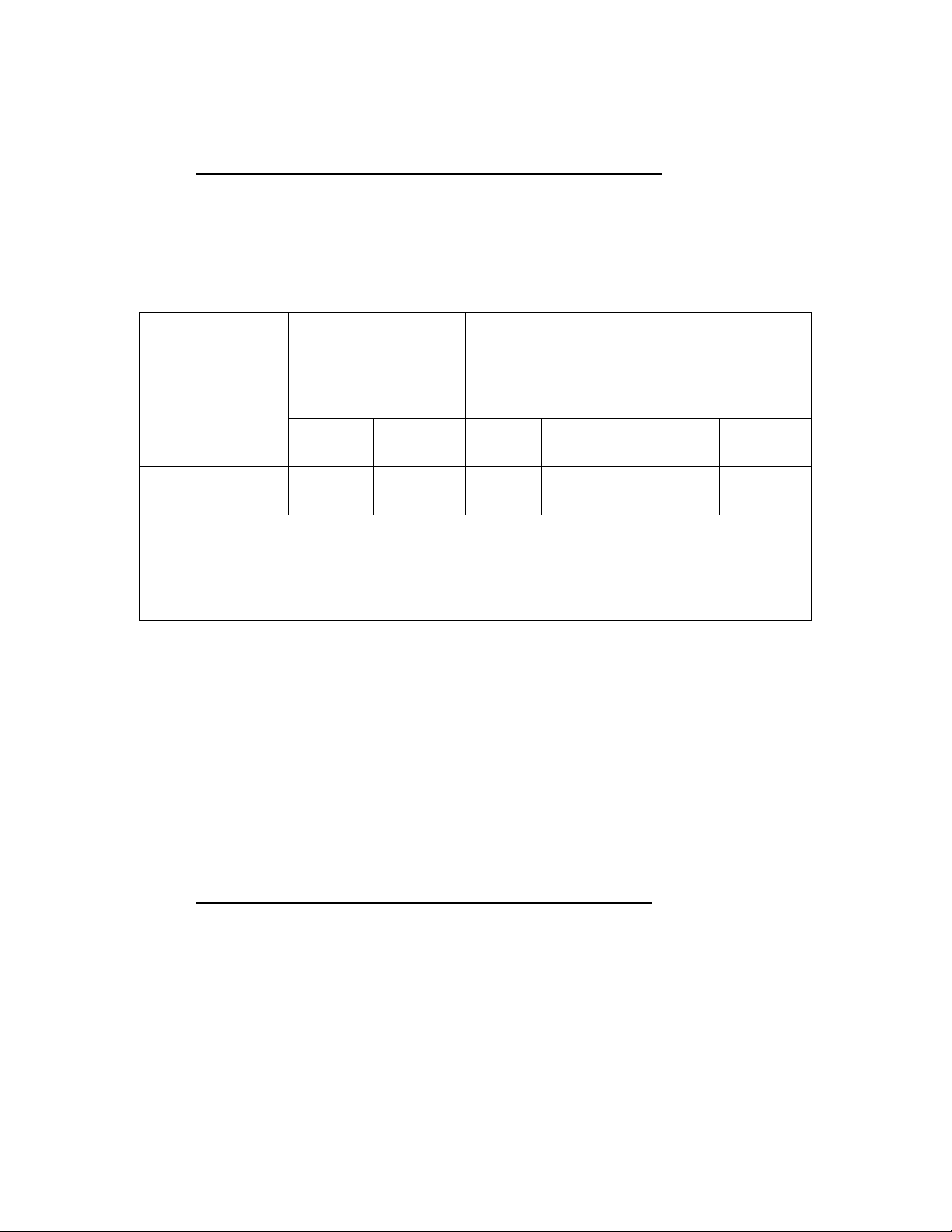
lượng làm bài của các học sinh (HS) phần Bất đẳng thức như sau:
Số HS không
làm được
Số HS chỉ làm
được các dạng
cơ bản
Số HS làm được
các dạng nâng
cao
SL % SL % SL %
Tống số HS: 5 2 40 2 40 1 20
Với kết quả này đã làm ảnh hưởng không nhỏ đến kết quả học tập môn
toán nói chung của HS ( Cụ thể qua lớp 9 chỉ có một HS tiếp tục bồi
dưỡng môn toán)
Qua bảng trên cho thấy, học sinh làm bài tập phần bất đẳng thức đạt
kết quả chưa cao, phương pháp học của các em và phương pháp GV định
hướng , hướng dẫn về phần này chưa được tốt nên ảnh hưởng đến chất
lượng của đội tuyển HSG. Chính vì vậy bản thân tôi có nhiều trăn trở, suy
nghĩ muốn tìm ra những phương pháp giải chuyên đề này để rèn kĩ năng
cho học sinh nhằm góp phần nâng cao hơn nữa chất lượng bồi dưỡng học
sinh giỏi môn Toán ở trường THCS.
2.1.2. Biện pháp thực hiện các giải pháp của đề tài
Để thực hiện các nhiệm vụ nghiên cứu nêu ở trên, tôi thực hiện các phương
pháp nghiên cứu sau :
Nghiên cứu lý thuyết về Tổng quan các tài liệu về lí luận dạy học, các văn
bản chỉ đạo về đổi mới, nâng cao chất lượng dạy học ở trường phổ thông,
các bài tập nâng cao, các bài tập chuyên chọn

Từ việc nghiên cứu lí thuyết lựa chọn các bài tập cơ bản, điển hình cho
mỗi dạng sau đó tổng hợp thành phương pháp giải cho mỗi dạng trong bài
toán bất đẳng thức
Nghiên cứu cơ sở lí luận về Bài tập bất đẳng thức ở trường phổ thông.
Nghiên cứu và khai thác một số bài tập cơ bản trong chuyên đề bồi dưỡng
HSG chuyên đề bất đẳng thức
Thiết kế và xây dựng các bài tập mẫu về toán bất đẳng thức trong chương
trình bồi dưỡng HSG môn Toán lớp 8
Nghiên cứu hiệu quả của việc áp dụng phương pháp giải bài toán bất đẳng
thức vào quá trình bồi dưỡng HSG môn Toán 8.
2.2. NỘI DUNG
2.2.1. Phương pháp 1 : Dùng định nghĩa
Kiến thức: Để chứng minh A > B. Ta lập hiệu A –B > 0
Lưu ý dựng hằng bất đẳng thức M 2
0 với M
Bài số1:Với mọi a,b lớn hơn 0
Chứng minh: a3+b3
ab(a+b)
Để chứng minh ta xét hiệu: a3+b3 – ab(a+b) = (a+b)(a2 – ab + b2) – ab(a+b)
= (a+b)( a2 –2ab + b2) = (a+b)(a-b)2
Vì a,b dương nên (a+b) > 0 , (a-b)2
0 suy ra (a+b)(a-b)2
0
Hay a3+b3
ab(a+b)
Dấu bằng xảy ra khi và chỉ khi a = b
Bài số 2: Chứng minh rằng với mọi xy ta luôn có : x2+ y2+1
xy+x+y
Xét hiệu
2 2
2 2
2
2 2
1 ( )
12 2 2 2 2 2
2
1
( ) 1 ( 1) 0
2
x y xy x y
x y xy x y
x y y x
Vì ( x - y)2
0 , (y-1)2
0 ,(x-1)2
0
Dấu bằng xảy ra khi và chỉ khi x = y = 1
Bài số 3: chứng minh rằng :
a)
2
22
22
baba ;
b)
2
222
33
cbacba
c) Hãy tổng quát bài toán

Giải: a) Ta xét hiệu
2
22
22
baba =
4
2
4
22222 bababa
=
abbaba 222
4
12222 =
0
4
12 ba Vậy
2
22
22
baba .
Dấu bằng xảy ra khi a = b
b)Ta xét hiệu
2
222
33
cbacba =
0
9
1222 accbba .
Vậy
2
222
33
cbacba . Dấu bằng xảy ra khi a = b =c
c)Tổng quát
2
21
22
2
2
1........
n
aaa
n
aaa nn
Bài số 4:
Chứng minh m,n,p,q ta đều có : m 2+ n 2+ p2+ q 2+1 m(n+p+q+1)
Giải:
01
4444
2
2
2
2
2
2
2
m
m
qmq
m
pmp
m
nmn
m
01
2222
2222
m
q
m
p
m
n
m (luôn đúng)
Dấu bằng xảy ra khi
01
2
0
2
0
2
0
2
m
q
m
p
m
n
m
2
2
2
2
m
m
q
m
p
m
n
1
2
qpn
m
Bài số 5:
1, 1.
Cho x y
Chứng minh: 2 2
1 1 2
1 1 1
x y xy
Xét hiệu : 2 2 2 2
1 1 2 1 1 1 1
1 1 1 1 1 1 1
x y xy x y xy xy
2 2
( ) ( )
(1 )(1 ) (1 )(1 )
x y x y x y
x xy y xy
2 2
2 2
( )(1 ) ( )(1 )
(1 )(1 )(1 )
x y x y y x y x
x y xy
2 2 2
2 2 2 2
( )( ) ( ) ( 1)
0
(1 )(1 )(1 ) (1 )(1 )(1 )
x y x xy y x y x y xy
x y xy x y xy
Vì x
1, 1
y
xy-1
0 và (x-y)2 nên bất đẳng thức cuối cùng đúng


























