
Chuyên đ: Tính ch t các đi m c c tr c a đ th hàm s ề ấ ể ự ị ủ ồ ị ố
4 2
y ax bx c= + +
và ng d ngứ ụ
------------------------------------------------------------------------------------------------------------------------------------------------------
TÍNH CH T CÁC ĐI M C C TR C A Đ TH HÀM SẤ Ể Ự Ị Ủ Ồ Ị Ố
4 2
y ax bx c= + +
VÀ NG D NGỨ Ụ
Các đ thi tuy n sinh vào Đi h c và Cao đng trong các năm g n đây, chúng taề ể ạ ọ ẳ ầ
th ng g p câu kh o sát hàm s ườ ặ ả ố
( )
4 2
0y ax bx c a= + +
và các v n đ liên quan đn cácấ ề ế
đi m c c tr c a đ th hàm s này. Đ giúp h c sinh ôn thi có hi u qu , bài vi t này đa raể ự ị ủ ồ ị ố ể ọ ệ ả ế ư
các tính ch t th ng g p c a các đi m c c tr c a hàm s ấ ườ ặ ủ ể ự ị ủ ố
4 2
y ax bx c= + +
và m t s ngộ ố ứ
d ng c a nó.ụ ủ
I. C S LÝ THUY TƠ Ở Ế
Xét hàm s ố
( )
4 2
0y ax bx c a= + +
trên
ᄀ
.
Ta có
( )
3 2
4 2 2 2y ax bx x ax b
= + = +
. Suy ra
2
0
02 0 (1)
x
yax b
=
= + =
đây chúng ta ch xét tr ng h p hay g p là đ th hàm s Ở ỉ ườ ợ ặ ồ ị ố
4 2
y ax bx c= + +
có ba
đi m c c tr phân bi t.ể ự ị ệ
Đ th hàm s ồ ị ố
4 2
y ax bx c= + +
có ba đi m c c tr phân bi t khi và ch khi ể ự ị ệ ỉ
0y=
có ba
nghi m phân bi t hay ph ng trình (1) có hai nghi m phân bi t khác 0 ệ ệ ươ ệ ệ
0ab <�
(*)
V i đi u ki n (*) ta có ớ ề ệ
0
0
2
x
yb
xa
=
= = −
. Suy ra đ th hàm s có ba đi m c c tr làồ ị ố ể ự ị
( )
0; A c
,
2
;
2 4
b b
B c
a a
� �
− − −
� �
� �
và
2
;
2 4
b b
C c
a a
� �
− −
� �
� �
.
Khi đó ta có
4
2
8
16
b ab
AB AC a
−
= =
và
2b
BC a
= −
.
Sau đây là m t s tính ch t th ng g p c a các đi m c c tr này.ộ ố ấ ườ ặ ủ ể ự ị
1) Đi u ki n đề ệ ể ba đi m c c tr A, B, C t o thành ba đnh c a m t tam giác vuông.ể ự ị ạ ỉ ủ ộ
Vì
AB AC=
nên tam giác ABC là tam giác cân t i ạA. Suy ra tam giác ABC là tam giác
vuông khi và ch khi ỉ
ᄀ
0
90BAC =
hay tam giác ABC vuông cân t i ạA.
Khi đó
2BC AB=
2 2
2BC AB=�
4
2
2 8
2. 16
b b ab
a a
−
− =�
3
8 0b a+ =�
Tính ch t 1:ấ Đ th hàm s ồ ị ố
4 2
y ax bx c= + +
có ba đi m c c tr t o thành ba đnh c a m tể ự ị ạ ỉ ủ ộ
tam giác vuông khi và ch khi ỉ
3
0
8 0
ab
b a
<
+ =
.
2) Đi u ki n đ ba đi m c c tr A, B, C t o thành ba đnh c a m t tam giác đu.ề ệ ể ể ự ị ạ ỉ ủ ộ ề
Ta có tam giác ABC là tam giác đu khi và ch khi ề ỉ
AB AC BC= =
2 2
AB BC=�
------------------------------------------------------------------------------------------------------------------------------------------------------
Th y giáo Nguy n Văn Thi t, tr ng THPT Vinh Xuân, Phú Vang, Th a Thiên Huầ ễ ế ườ ừ ế
1

Chuyên đ: Tính ch t các đi m c c tr c a đ th hàm s ề ấ ể ự ị ủ ồ ị ố
4 2
y ax bx c= + +
và ng d ngứ ụ
------------------------------------------------------------------------------------------------------------------------------------------------------
4
2
8 2
16
b ab b
a a
−= −�
3
24 0b a+ =�
.
Tính ch t 2:ấ Đ th hàm s ồ ị ố
4 2
y ax bx c= + +
có ba đi m c c tr t o thành ba đnh c a m tể ự ị ạ ỉ ủ ộ
tam giác đu khi và ch khi ề ỉ
3
0
24 0
ab
b a
<
+ =
.
3) Đi u ki n đ ba đi m c c tr A, B, C t o thành ba đnh c a m t tam giác cân có m tề ệ ể ể ự ị ạ ỉ ủ ộ ộ
góc
α
cho tr c.ướ
Có ba tr ng h p x y ra.ườ ợ ả
Tr ng h p 1:ườ ợ
0
90
α
>
.
Khi đó tam giác ABC là tam giác tù. Vì tam giác ABC cân t i ạA nên tam giác ABC có
m t góc ộ
0
90
α
>
khi và ch khi ỉ
ᄀ
BAC
α
=
.
Áp d ng đnh lý côsin vào tam giác ụ ị ABC ta có
ᄀ
222
2 . .cosBC AB AC AB AC BAC= + −
( )
2 2
2 1 cosBC AB
α
= −�
( )
4
2
2 8
2. 1 cos
16
b b ab
a a
α
−
− = −�
( )
( )
3
16 8 1 cosa b a
α
− = − −�
( )
3 3
8 8 cos 0b a b a
α
+ − − =�
.
Tr ng h p 2:ườ ợ
0
90
α
=
( ta đã xét tính ch t 1)ở ấ
Tr ng h p 3:ườ ợ
0
90
α
<
.
+ N u ế
ᄀ
ᄀ
B C
α
= =
thì
ᄀ
0
180 2A
α
= −
, suy ra
( )
0
cos cos 180 2 cos 2A
α α
= − = −
.
Áp d ng đnh lý côsin vào tam giác ụ ị ABC ta có
ᄀ
222
2 . .cosBC AB AC AB AC BAC= + −
( )
2 2
2 1 cos 2BC AB
α
= +�
( )
4
2
2 8
2. 1 cos 2
16
b b ab
a a
α
−
− = +�
( )
( )
3
16 8 1 cos 2a b a
α
− = − +�
( )
3 3
8 8 cos 2 0b a b a
α
+ + − =�
.
+ N u ế
ᄀ
A
α
=
thì t ng t tr ng h p 1, ta có ươ ự ườ ợ
( )
3 3
8 8 cos 0b a b a
α
+ − − =
.
Tính ch t 3ấ. Đ th hàm s ồ ị ố
4 2
y ax bx c= + +
có ba đi m c c tr A, B, C t o thành ba đnhể ự ị ạ ỉ
c a m t tam giác cân có m t góc ủ ộ ộ
α
cho tr c khi và ch khi ướ ỉ
0ab <
và
ho c ặ
( )
3 3
8 8 cos 0b a b a
α
+ − − =
n u ế
0
90
α
>
ho cặ
3
8 0b a+ =
n u ế
0
90
α
=
ho cặ
( )
3 3
8 8 cos 2 0b a b a
α
+ + − =
n u ế
ᄀ
ᄀ
0
90B C
α
= = <
ho cặ
( )
3 3
8 8 cos 0b a b a
α
+ − − =
n u ế
ᄀ
0
90A
α
= <
.
4) Đi u ki n đ ba đi m c c tr A, B, C th a mãn ề ệ ể ể ự ị ỏ
BC OA=
(v i O là g c t a đớ ố ọ ộ)
Ta có
BC OA=
2 2
BC OA=�
2
2bc
a
− =�
2
2 0ac b+ =�
.
------------------------------------------------------------------------------------------------------------------------------------------------------
Th y giáo Nguy n Văn Thi t, tr ng THPT Vinh Xuân, Phú Vang, Th a Thiên Huầ ễ ế ườ ừ ế
2
Chuyên đ: Tính ch t các đi m c c tr c a đ th hàm s ề ấ ể ự ị ủ ồ ị ố
4 2
y ax bx c= + +
và ng d ngứ ụ
------------------------------------------------------------------------------------------------------------------------------------------------------
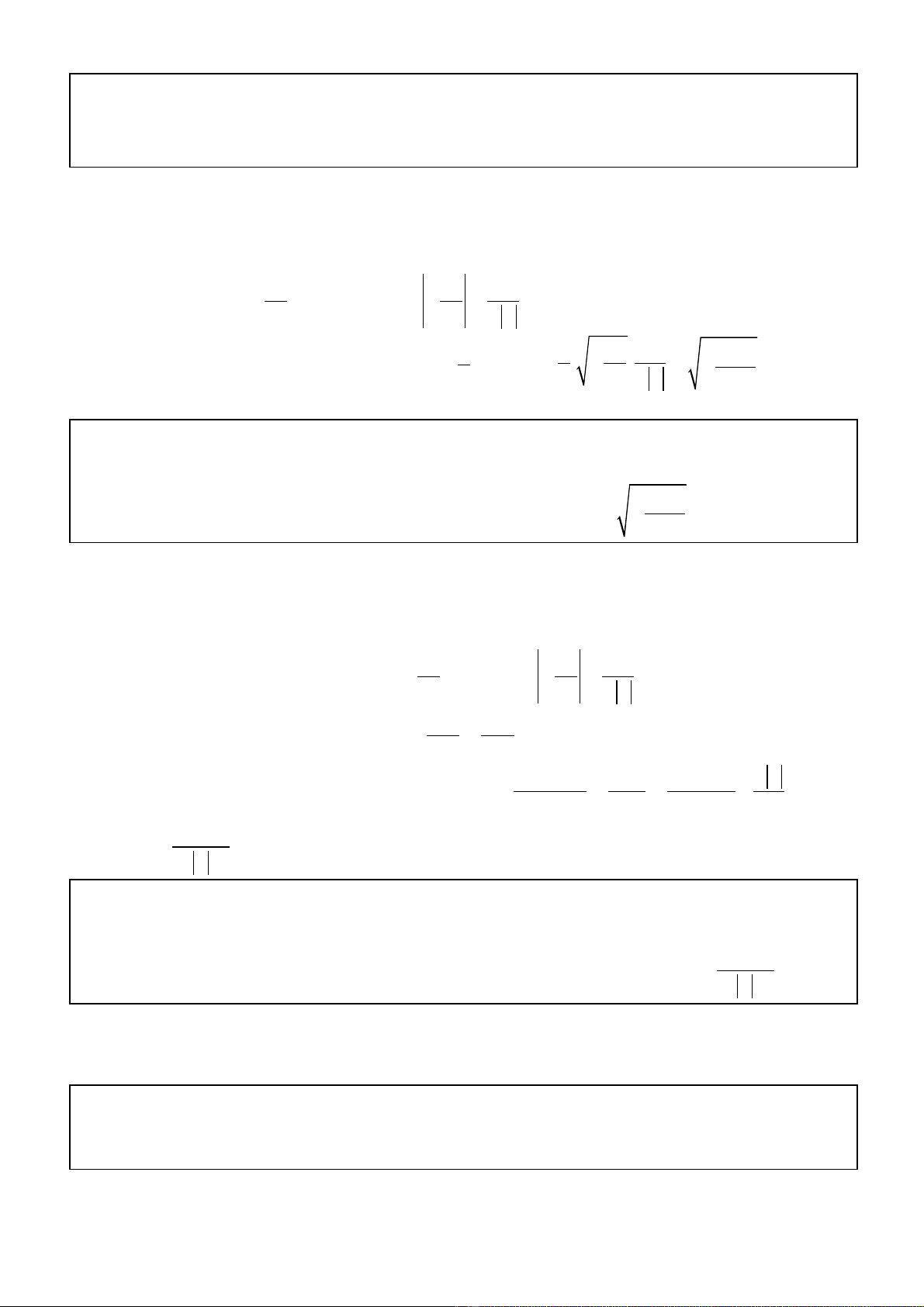
Tính ch t 4ấ. Đ th hàm s ồ ị ố
4 2
y ax bx c= + +
có ba đi m c c tr A, B, C ể ự ị th a mãn đi uỏ ề
ki n ệ
BC OA=
(v i O là g c t a đớ ố ọ ộ) khi và ch khiỉ
2
0
2 0
ab
ac b
<
+ =
.
5) Đi u ki n đề ệ ể ba đi m c c tr A, B, C t o thành ba đnh c a m t tam giác và tính di nể ự ị ạ ỉ ủ ộ ệ
tích tam giác đó.
G i ọH là giao đi m c a ể ủ BC v i tr c ớ ụ Oy thì AH là đng cao c a tam giác ườ ủ ABC. Khi đó
H có t a đ ọ ộ
2
0; 4
b
H c a
� �
−
� �
� �
. Suy ra
2 2
4 4
b b
AH a a
= − =
.
V y di n tích tam giác ậ ệ ABC là
1.
2
ABC
S BC AH=
2
1 2
. .
2 4
b b
a a
= −
5
3
32
b
a
= −
.
Tính ch t 5ấ. Đ th hàm s ồ ị ố
4 2
y ax bx c= + +
có ba đi m c c tr A, B, C t o thành ba đnhể ự ị ạ ỉ
c a m t tam giác có di n tích là S cho tr c khi và ch khi ủ ộ ệ ướ ỉ
5
3
0
32
ab
b
Sa
<
= −
.
6) Đi u ki n đề ệ ể ba đi m c c tr A, B, C t o thành ba đnh c a m t tam giác và tính bánể ự ị ạ ỉ ủ ộ
kính đng tròn ngo i ti p tam giác ABC.ườ ạ ế
G i ọR là bán kính đng tròn ngo i ti p tam giác ườ ạ ế ABC và H là giao đi m c a ể ủ BC v iớ
tr c ụOy. Khi đó H có t a đ là ọ ộ
2
0; 4
b
H c a
� �
−
� �
� �
và
2 2
4 4
b b
AH a a
= − =
.
T tam giác vuông ừAHC, ta có
ᄀ
sin AH AH
ACH AC AB
= =
.
Áp d ng đnh lý sin vào tam giác ụ ị ABC ta đc ượ
ᄀ
2 4
2 2
4
8
216
sin
a
AB AB b ab
RAH a b
ACH
−
= = =
Suy ra
3
8
8
b a
Ra b
−
=
.
Tính ch t 6.ấ Đ th hàm s ồ ị ố
4 2
y ax bx c= + +
có ba đi m c c tr A, B, C t o thành ba đnhể ự ị ạ ỉ
c a m t tam giác có bán kính đng tròn ngo i ti p là R khi và ch khi ủ ộ ườ ạ ế ỉ
3
0
8
8
ab
b a
Ra b
<
−
=
.
II. NG D NGỨ Ụ
Ví d 1ụ. (Câu 1 đ thi TSĐH năm 2012 kh i A và kh i A1ề ố ố )
Cho hàm s ố
( )
4 2 2
2 1y x m x m= − + +
(1), v i ớm là tham s th c.ố ự
Tìm m đ đ th hàm s (1) có ba đi m c c tr t o thành ba đnh c a m t tam giác vuông.ể ồ ị ố ể ự ị ạ ỉ ủ ộ
L i gi iờ ả .
------------------------------------------------------------------------------------------------------------------------------------------------------
Th y giáo Nguy n Văn Thi t, tr ng THPT Vinh Xuân, Phú Vang, Th a Thiên Huầ ễ ế ườ ừ ế
3

Chuyên đ: Tính ch t các đi m c c tr c a đ th hàm s ề ấ ể ự ị ủ ồ ị ố
4 2
y ax bx c= + +
và ng d ngứ ụ
------------------------------------------------------------------------------------------------------------------------------------------------------
Áp d ng tính ch t 1, đ th hàm s (1) có ba đi m c c tr t o thành ba đnh c a m t tam giácụ ấ ồ ị ố ể ự ị ạ ỉ ủ ộ
vuông khi và ch khi ỉ
3
0
8 0
ab
b a
<
+ =
( )
( )
3
2 1 0
8 1 8 0
m
m
− + <�
− + + =
( )
3
1
1 1
m
m
> −
+ =
1
0
m
m
> −
=
0m=�
Ví d 2ụ. (Câu 1 đ thi TSĐH năm 2011 kh i Bề ố )
Cho hàm s ố
( )
4 2
2 1y x m x m= − + +
(1), m là tham s . ố
Tìm m đ đ th hàm s (1) có ba đi m c c tr ể ồ ị ố ể ự ị A, B, C sao cho
OA BC
=
; trong đó O
là g c t a đ , ố ọ ộ A là đi m c c tr thu c tr c tung, ể ự ị ộ ụ B và C là hai đi m c c tr còn l i.ể ự ị ạ
L i gi iờ ả .
Áp d ng tính ch t 4, đ th hàm s (1) có ba đi m c c tr ụ ấ ồ ị ố ể ự ị A, B, C sao cho
OA BC=
khi
và ch khi ỉ
2
0
2 0
ab
ac b
<
+ =
( )
( )
2
2 1 0
4 1 0
m
m m
− + <�
− + =
2
1
4 4 0
m
m m
> −
− − =
2 2 2m=� �
.
Ví d 3.ụ Cho hàm s ố
4 2
2 3y x mx= − −
(1)
Tìm m đ đ th hàm s (1) có ba đi m c c tr và bán kính đng tròn ngo i ti p tamể ồ ị ố ể ự ị ườ ạ ế
giác t o b i các đi m c c tr đó đt giá tr nh nh t.ạ ở ể ự ị ạ ị ỏ ấ
L i gi iờ ả .
Áp d ng tính ch t 6, đ th hàm s (1) có ba đi m c c tr và bán kính đng trònụ ấ ồ ị ố ể ự ị ườ
ngo i ti p tam giác t o b i các đi m c c tr là ạ ế ạ ở ể ự ị R khi và ch khi ỉ
3
0
8
8
ab
b a
Ra b
<
−
=
( )
( )
3
2 0
2 8
8 2
m
m
Rm
− <
− −
=
−
3
0
1
2
m
m
Rm
>
+
=
. Suy ra
2
1 1
2
R m m
� �
= +
� �
� �
.
S d ng b t đng th c Cauchy cho ba s d ng, ta cóử ụ ấ ẳ ứ ố ươ
2 2 3
3
3
1 1 1 1 1 1 3 1 3
.3. . . . . 2
2 2 2 2 2 2 2 4
4
R m m
m m m m
� �
= + + = =
� �
� �
.
V y ậ
2
3
3 1
min . 2
4 2
R m m
= =�
3
3
1 1
22
m m= =� �
.
Ví d 4ụ. Cho hàm s ố
4 2
2 1y x mx= − +
(1)
Tìm các giá tr c a tham s ị ủ ố m đ đ th hàm s (1) có ba đi m c c tr và đng trònể ồ ị ố ể ự ị ườ
đi qua ba đi m này có bán kính b ng 1.ể ằ
L i gi iờ ả .
------------------------------------------------------------------------------------------------------------------------------------------------------
Th y giáo Nguy n Văn Thi t, tr ng THPT Vinh Xuân, Phú Vang, Th a Thiên Huầ ễ ế ườ ừ ế
4
Chuyên đ: Tính ch t các đi m c c tr c a đ th hàm s ề ấ ể ự ị ủ ồ ị ố
4 2
y ax bx c= + +
và ng d ngứ ụ
------------------------------------------------------------------------------------------------------------------------------------------------------
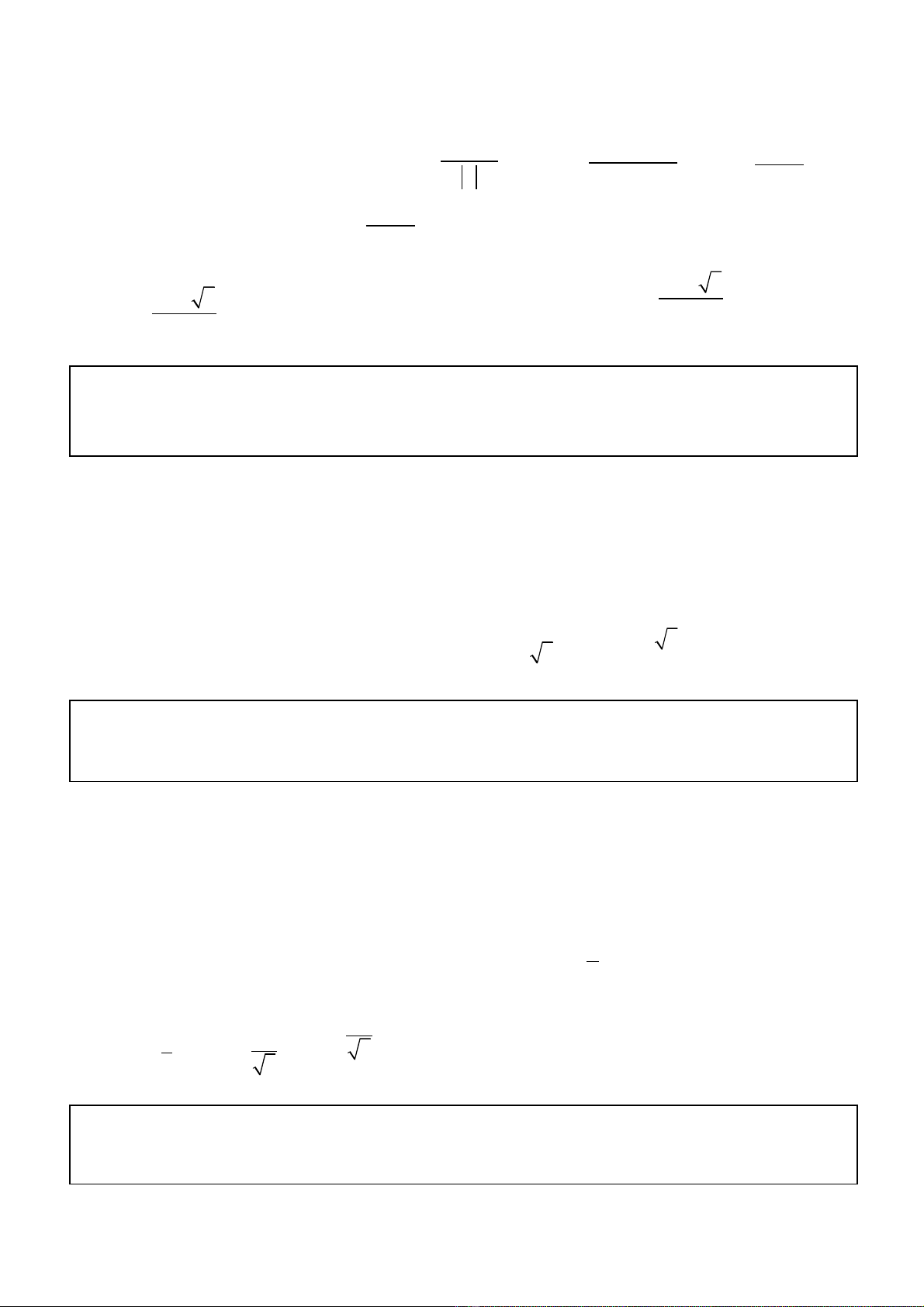
Áp d ng tính ch t 6, đ th hàm s (1) có ba đi m c c tr và đng tròn đi qua baụ ấ ồ ị ố ể ự ị ườ
đi m này có bán kính ểR khi và ch khi ỉ
3
0
8
8
ab
b a
Ra b
<
−
=
hay
( )
( )
3
2 0
2 8
8 2
m
m
Rm
− <
− −
=
−
3
0
1
2
m
m
Rm
>
+
=
Theo đ bài ta có ề
1R=
, suy ra
3
1
12
m
m
+
=
3
2 1 0m m− + =�
( )
( )
2
1 1 0m m m− + − =�
1
1 5
2
m
m
=
−
=
. Đi chi u v i đi u ki n ố ế ớ ề ệ
0m>
ta đc ượ
1m=
,
1 5
2
m− +
=
.
Ví d 5ụ. Cho hàm s ố
( )
4 2 2
2 2 5 5y x m x m m= + − + − +
( )
m
C
V i nh ng giá tr nào c a ớ ữ ị ủ m thì đ th ồ ị
( )
m
C
có đi m c c đi và đi m c c ti u, đngể ự ạ ể ự ể ồ
th i các đi m c c đi và đi m c c ti u l p thành m t tam giác đu.ờ ể ự ạ ể ự ể ậ ộ ề
L i gi iờ ả .
Áp d ng tính ch t 2, đ th ụ ấ ồ ị
( )
m
C
có đi m c c đi và đi m c c ti u, đng th i cácể ự ạ ể ự ể ồ ờ
đi m ể
c c đi và đi m c c ti u l p thành m t tam giác đu khi và ch khi ự ạ ể ự ể ậ ộ ề ỉ
3
0
24 0
ab
b a
<
+ =
( )
( )
3
2 2 0
8 2 24 0
m
m
− <�
− + =
( )
3
2
2 3
m
m
<
− = −
3
2
2 3
m
m
<
= −
3
2 3m= −�
.
Ví d 6ụ. Cho hàm s ố
4 2
2 1y x mx= − + +
Tìm m đ đ th hàm s có ba đi m c c tr t o thành ba đnh c a m t tam giác có m tể ồ ị ố ể ự ị ạ ỉ ủ ộ ộ
góc b ng ằ
0
120
.
L i gi iờ ả .
Theo tính ch t 3, đ th hàm s có ba đi m c c tr t o thành ba đnh c a m t tam giác ấ ồ ị ố ể ự ị ạ ỉ ủ ộ
có m t góc ộ
0
120
α
=
khi và ch khi ỉ
( )
3 3
0
8 8 cos 0
ab
b a b a
α
<
+ − − =
( )
3 3 0
2 0
8 8 8 8 cos120 0
m
m m
− <
− − + =
( )
3 3
0
1
8 8 8 8 0
2
m
m m
>
� �
− − + − =
� �
� �
3
0
12 4 0
m
m
>
− =
3
0
1
3
m
m
>
=
3
0
1
3
m
m
>
=
3
1
3
m=�
.
Ví d 7ụ. Cho hàm s ố
4 2
2 2y x mx m= − + +
.
Tìm m đ đ th hàm s có ba đi m c c tr t o thành ba đnh c a m t tam giác cóể ồ ị ố ể ự ị ạ ỉ ủ ộ
di n tích b ng 32. ệ ằ
------------------------------------------------------------------------------------------------------------------------------------------------------
Th y giáo Nguy n Văn Thi t, tr ng THPT Vinh Xuân, Phú Vang, Th a Thiên Huầ ễ ế ườ ừ ế
5





















