KiÓm tra bµi cò
1) Cho (d) có ph ng trình tham s : ươ ố
Hãy ch ra m t đi m thu c d và m t VTCP c a (d)?ỉ ộ ể ộ ộ ủ
2 5
4 6
x t
y t
= +
= +
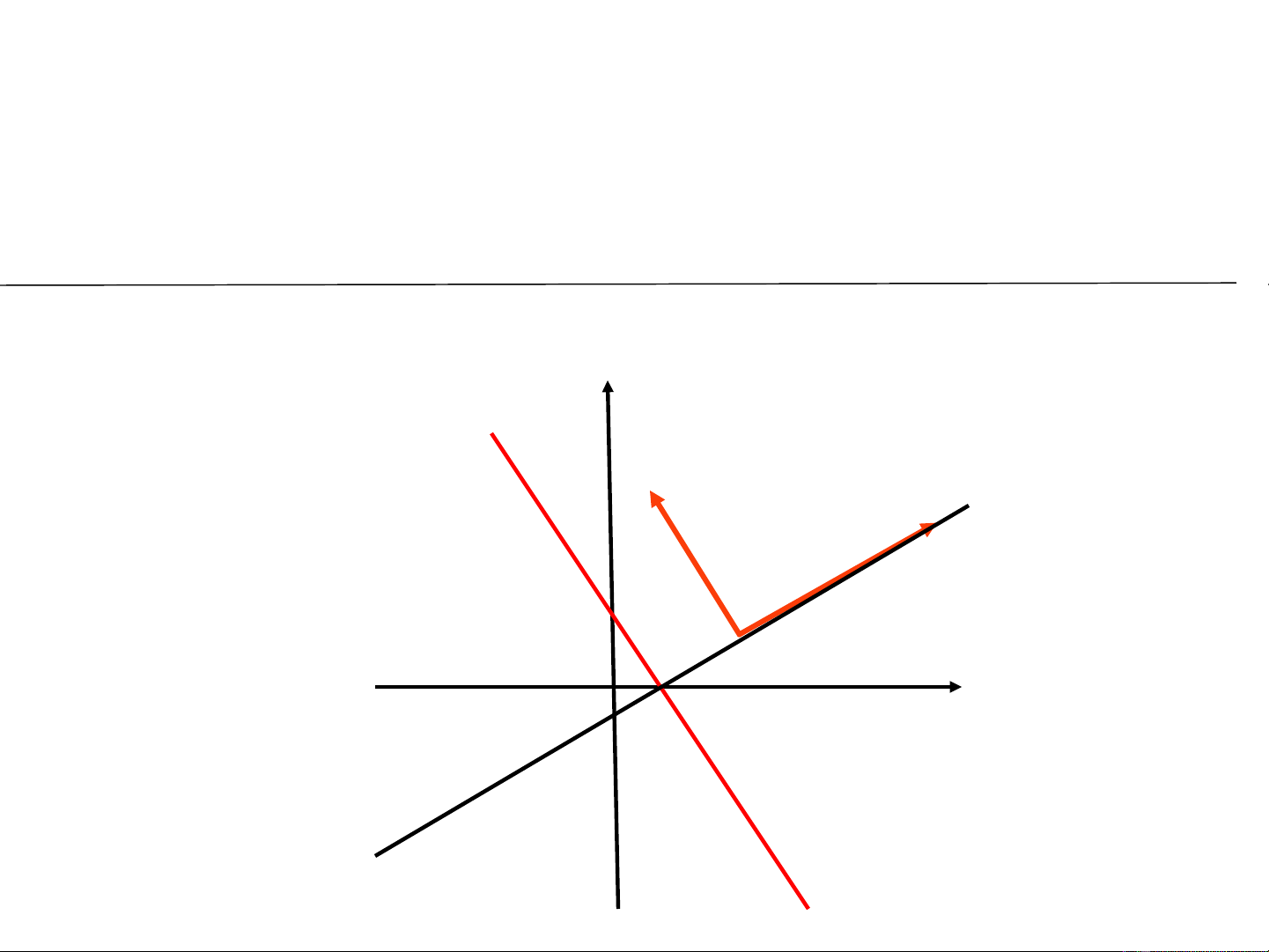
2) Ch ng minh r ng ứ ằ
( )
6; 5n
= −
r
vuông góc v i ớ VTCP c a đ ng th ng ủ ườ ẳ
(d).
n
r
u
r
O
d
y
x
n
r
u
r
O
d
y
x
3) Véc t pháp tuy n c a đ ng th ngơ ế ủ ườ ẳ
Bài 1:
Bài 1:
PH NG TRÌNH Đ NG TH NG (T3)ƯƠ ƯỜ Ẳ
PH NG TRÌNH Đ NG TH NG (T3)ƯƠ ƯỜ Ẳ
+) M t đ ng th ng hoàn toàn ộ ườ ẳ
đ c xác đ nh khi bi t m t đi m và m t ượ ị ế ộ ể ộ
VTPT c a nóủ.
Chú ý:
Chú ý: +) N u ế là vect pháp tuy n ơ ế
c a đt ủd thì cũng là vect pháp ơ
tuy n c a đt ế ủ d. M t đt có vô s vect ộ ố ơ
pháp tuy n. ế
. ( 0)k n k
r
n
r
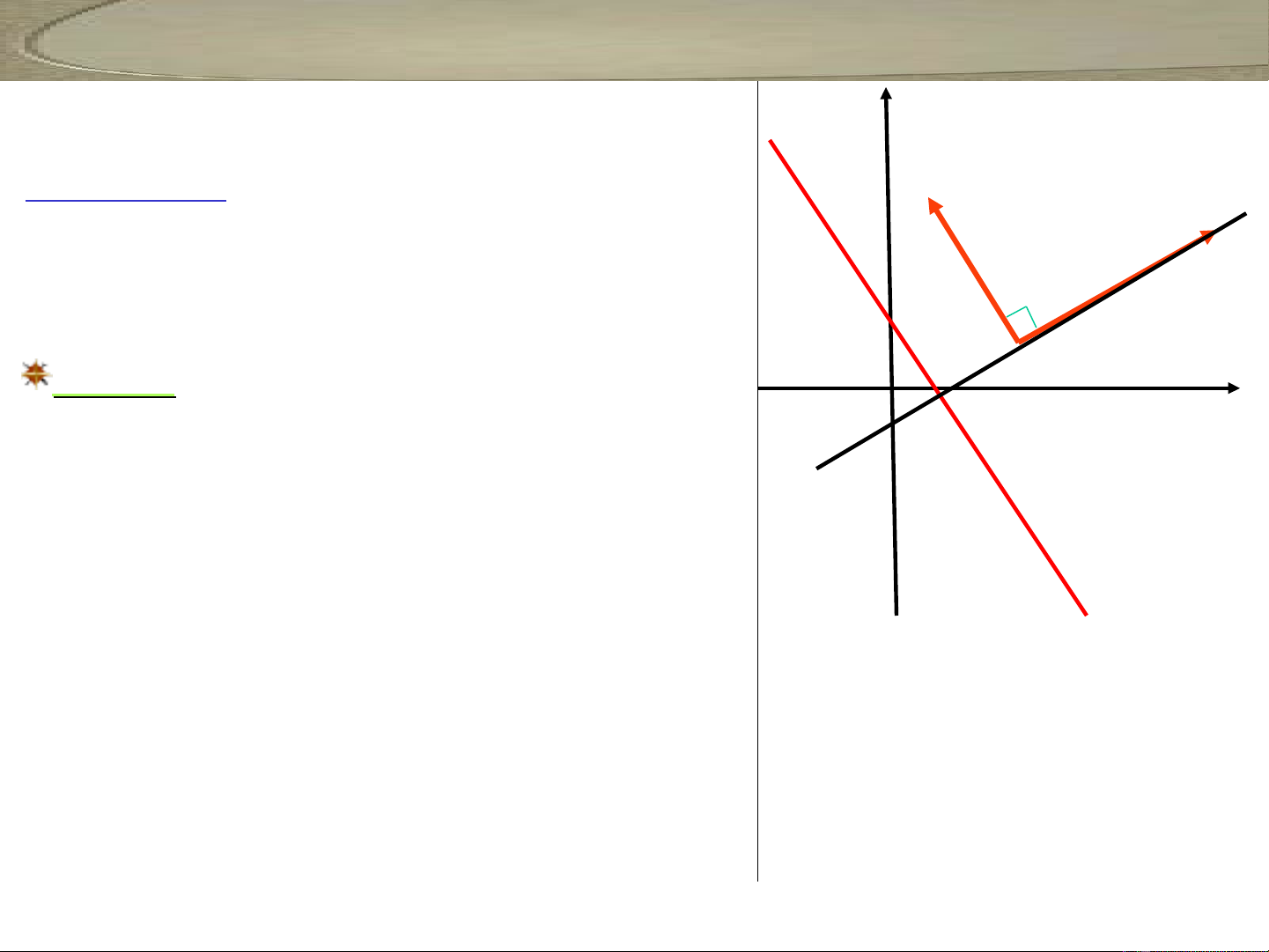
Đ nh nghĩaị: Véct đ c g i là véc t ơ ượ ọ ơ
pháp tuy n c a đ ng th ng ế ủ ườ ẳ d n u ế
và vuông góc v i VTCP c a ớ ủ d
0n
r r
n
r
n
r
u
r
O
d
y
x
4) Ph ng trình t ng quát c a ươ ổ ủ
đ ng th ngườ ẳ
Bài 1:
Bài 1:
PH NG TRÌNH Đ NG TH NG (T3)ƯƠ ƯỜ Ẳ
PH NG TRÌNH Đ NG TH NG (T3)ƯƠ ƯỜ Ẳ
M0
x0
y0
M
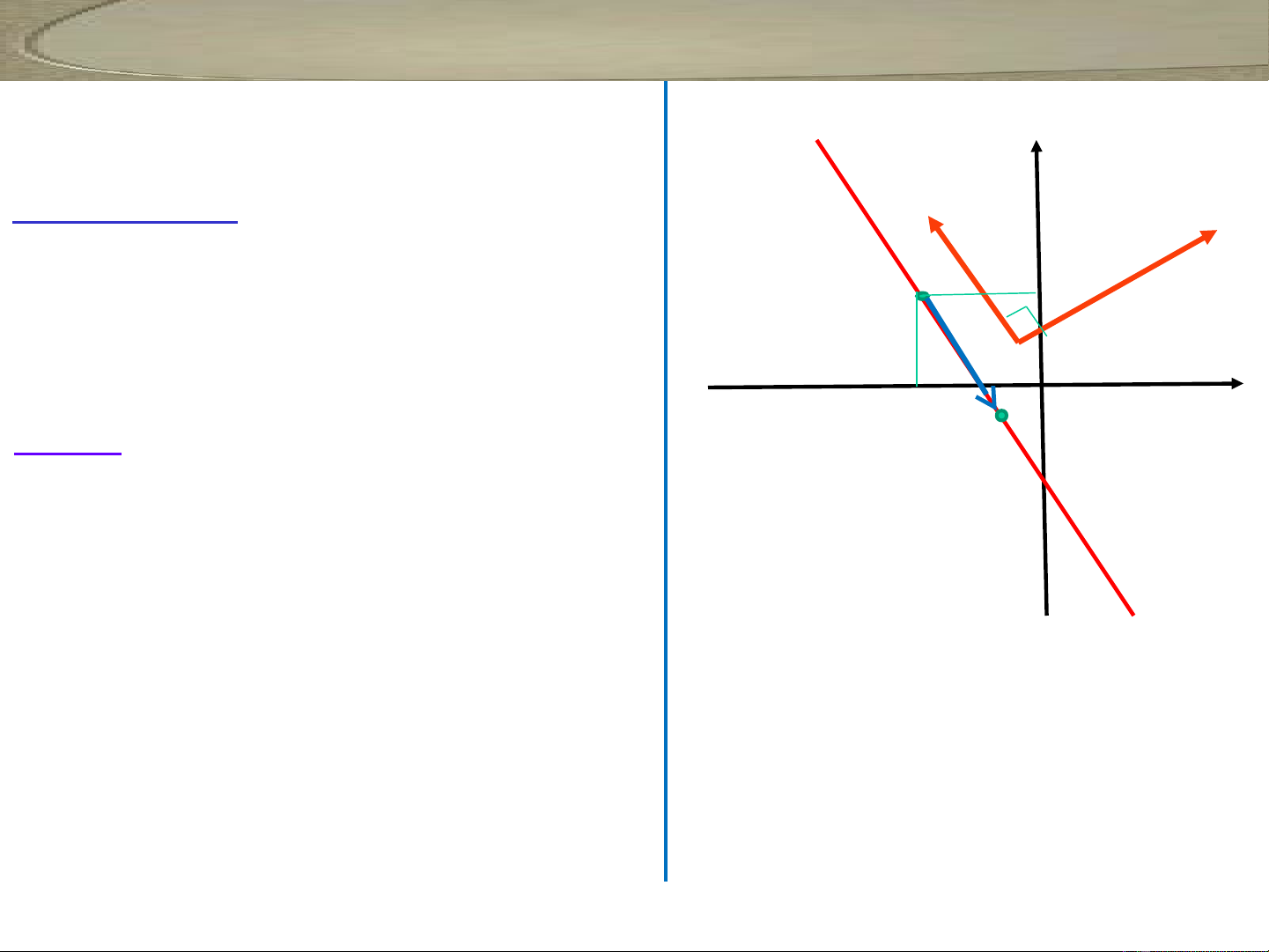
Cho đt d đi qua đi m Mể0(x0;y0)
nh n làm véct pháp ậ ơ
tuy n, tìm đi u ki n c a x, y đ ế ề ệ ủ ể
M(x,y) n m trên đt ằd ?
( ; )n a b
r
Đ nh nghĩa: ịPh ng trìnhươ
ax + by + c = 0 (1) (a2 + b2 0)
đ c g i là ượ ọ ph ng trình t ng ươ ổ
quát c a đ ng th ng.ủ ườ ẳ
Chú ý:
+) Đ ng th ng d có pt (1) thì d có ườ ẳ
VTPT và VTCP là
ho cặ
( ; )n a b
r
( ; )u b a
−
r
( ; )u b a
−
r
+) N u ếd đi qua M0(x0;y0) và có
VTPT thì ph ng trình ươ
c a d là:ủ
( ; )n a b
r
( ) ( )
0 0
0a x x b y y
− + − =
4) Ph ng trình t ng quát c a ươ ổ ủ
đ ng th ngườ ẳ
Bài 1:
Bài 1:
PH NG TRÌNH Đ NG TH NG (T3)ƯƠ ƯỜ Ẳ
PH NG TRÌNH Đ NG TH NG (T3)ƯƠ ƯỜ Ẳ
Đ nh nghĩa: ịPh ng trìnhươ
ax + by + c = 0 (1) (a2 + b2 0)
đ c g i là ượ ọ ph ng trình t ng ươ ổ
quát c a đ ng th ng.ủ ườ ẳ
Ví d 1ụ: L p PTTQ c a đ ng ậ ủ ườ
th ng đi qua đi m và có VTPT:ẳ ể
a) M(-2;3),
b) M(-1;2),
(5; 1)n
−
r
( 2;3)n
−
r
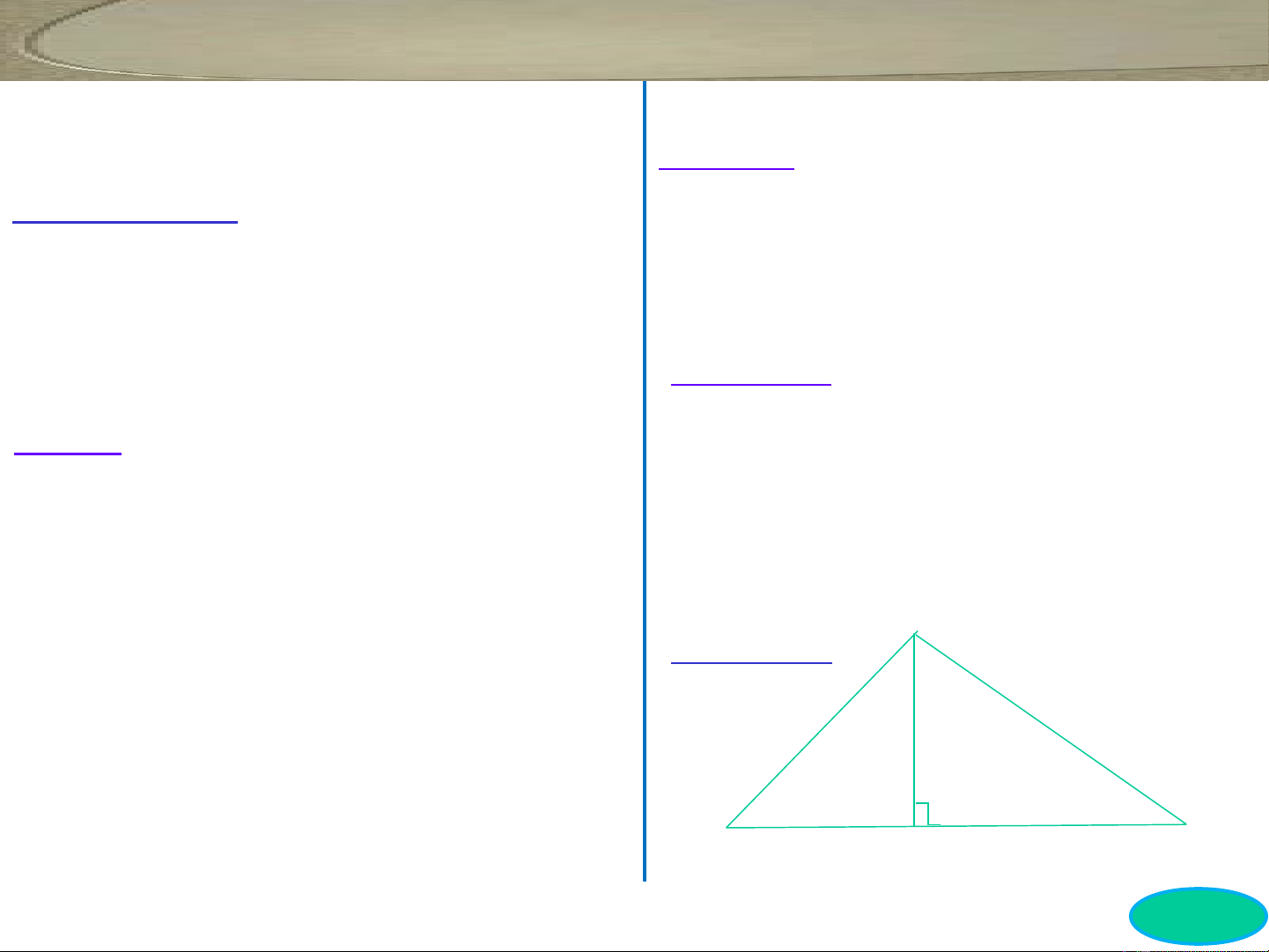
Ví d 2: ụCho tam giác có ba đ nh ỉ
A(-1;-1), B(-1;3), C(2;-4) vi t ế
PTTQ c a :ủ
a)Đ ng cao k t B?ườ ẻ ừ
b)Đ ng th ng AB?ườ ẳ
A
B
C
H
Chú ý:
+) Đ ng th ng d có pt (1) thì d có ườ ẳ
VTPT và VTCP là
ho cặ
( ; )n a b
r
( ; )u b a
−
r
( ; )u b a
−
r
+) N u ếd đi qua M0(x0;y0) và có
VTPT thì ph ng trình ươ
c a d là:ủ
( ; )n a b
r
( ) ( )
0 0
0a x x b y y
− + − =
Ví d 3: ụCho đ ng th ng d ườ ẳ
có PTTQ: 3x + 2y + 5 = 0.
a) Tìm VTCP c a d?ủ
b) Chuy n v PTTS ?ể ề