intTypePromotion=1
zunia.vn Tuyển sinh 2024 dành cho Gen-Z zunia.vn zunia.vn
ADSENSE
 » 
 » 

Bài giảng Bài tập Trường điện từ: Chương 3 - Lê Minh Cường

Chia sẻ: Thị Huyền | Ngày: | Loại File: PDF | Số trang:17

Thêm vào BST
Báo xấu
379
lượt xem 45
download
 
  Download Vui lòng tải xuống để xem tài liệu đầy đủ

Đến với "Bài giảng Bài tập Trường điện từ: Chương 3" của tác giả Lê Minh Cường các bạn sẽ được tham khảo 26 bài tập về cường độ từ trường trong toàn không gian; năng lượng từ trường tích lũy trong ống trụ; điện môi đơn vị dài; cường độ từ trường trong các miền; vecto cảm ứng từ;... Hy vọng tài liệu là nguồn thông tin hữu ích cho quá trình học tập và nghiên cứu của các bạn.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng Bài tập Trường điện từ: Chương 3 - Lê Minh Cường

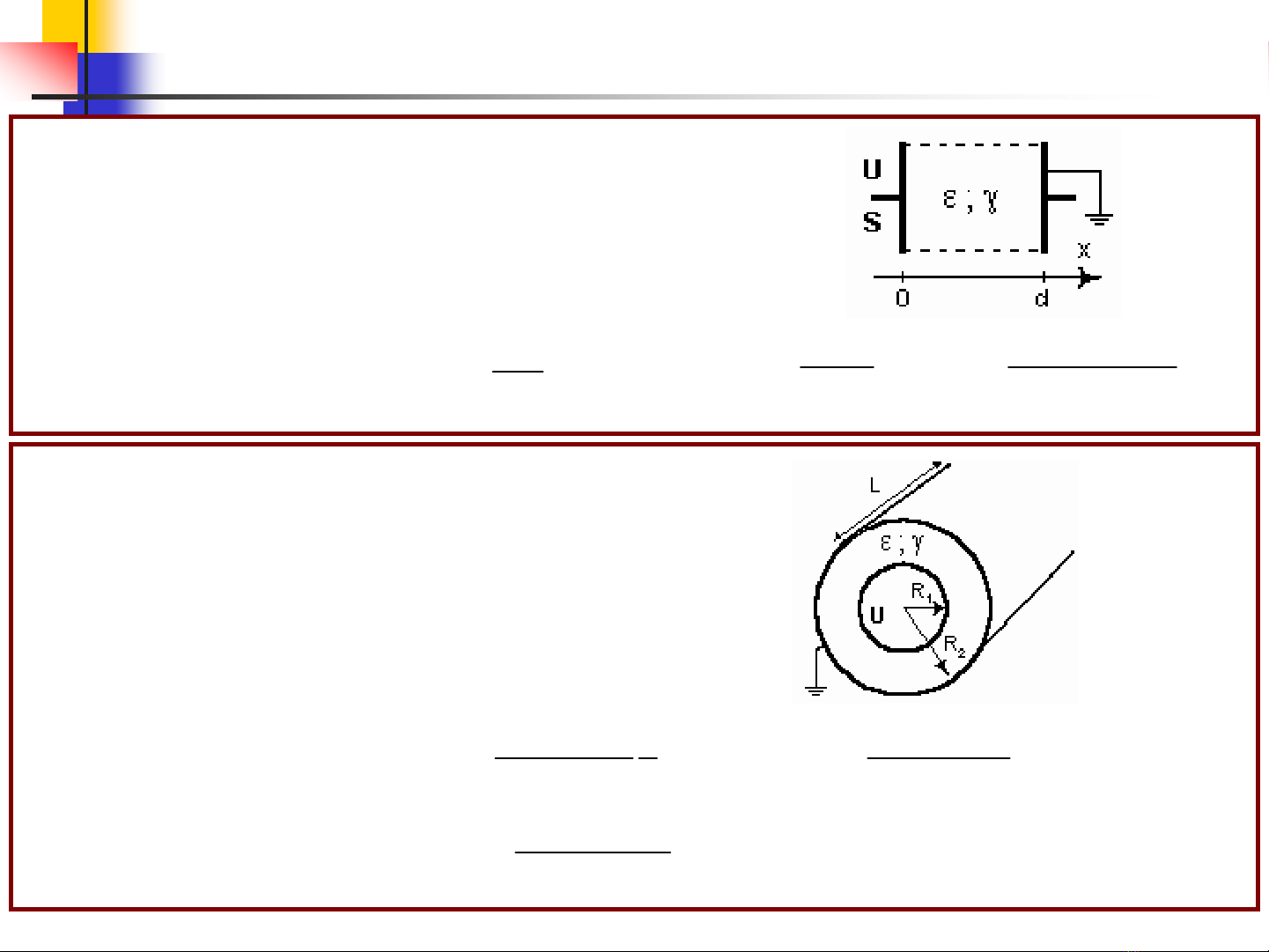
  1. BAØI TẬP CHƯƠNG 3 3.1: Tuï ñieän phaúng , ñieän moâi thöïc , coù : ε = const , → → → γ = 2γ0d./(x + d) , γ0 = const , tìm : a) J , E , P trong ñieän moâi ? b) ρ vaø ρlk trong ñieän moâi thöïc ? →2U → 2ε U 2(ε 0 − ε )U (ÑS: a) E = ( x + d ) x b) i ρ = ; ρ lk = ) 3d 2 3d 2 3d 2 3.2: Tuï ñieän truï , ñieän moâi thöïc , ε, γ = const , tìm : → → → a) J , E , D , ϕ trong ñieän moâi ? b) Doøng roø vaø Rcñ cuûa tuï ? c) Coâng suaát toån hao treân ñôn vò daøi ? d) ρ vaø ρlk trong ñieän moâi thöïc ? → U 1→ ln( R2 /R1 ) (ÑS: a) E = ir b) Rcd = ln(R 2 / R1 ) r 2πγ L 2πγ U 2 c) PJ = d) ρ = 0 ; ρ lk = 0 ) ln(R 2 /R 1 ) Problem_ch3 1
  2. BAØI TẬP CHƯƠNG 3 3.3: Tuï phaúng , dieän tích coát tuï S, khoaûng caùch d. Coát tuï noái ñaát taïi x = 0 , taïi x = d coù theá ñieän U. Giöõa 2 coát tuï laáp ñaày ñieän moâi thöïc coù γ = γ0 , ε = 3ε0d/(x + d) , vôùi γ0 = const. Tìm : a) ρ vaø ρlk trong ñieän moâi thöïc ? b) Coâng suaát toån hao nhieät PJ ? 3ε 0 U U 2 S (ÑS: a) ρ= ; ρ lk = − ρ b) P = γ ) (x + d ) 2 J 0 d 3.4: Tuï phaúng , ñieän moâi thöïc , ε = 4ε0 , γ = γ0.(1 + kx) , vôùi γ0 = 10-10 (S/m); k = 20 (m-1), tuï ñaët döôùi ñieän aùp U = 200 (V), khoaûng caùch d = 0,5 (cm), tìm : a) Theá ñieän trong ñieän moâi thöïc ? b) Maät ñoä ñieän tích töï do ρ trong ñieän moâi thöïc ? 29, 7 (ÑS: a) ϕ = 2098, 4. ln (1 + 20 x ) b) ρ = (µ C / m3 ) ) (1 + 20 x ) 2 Problem_ch3 2
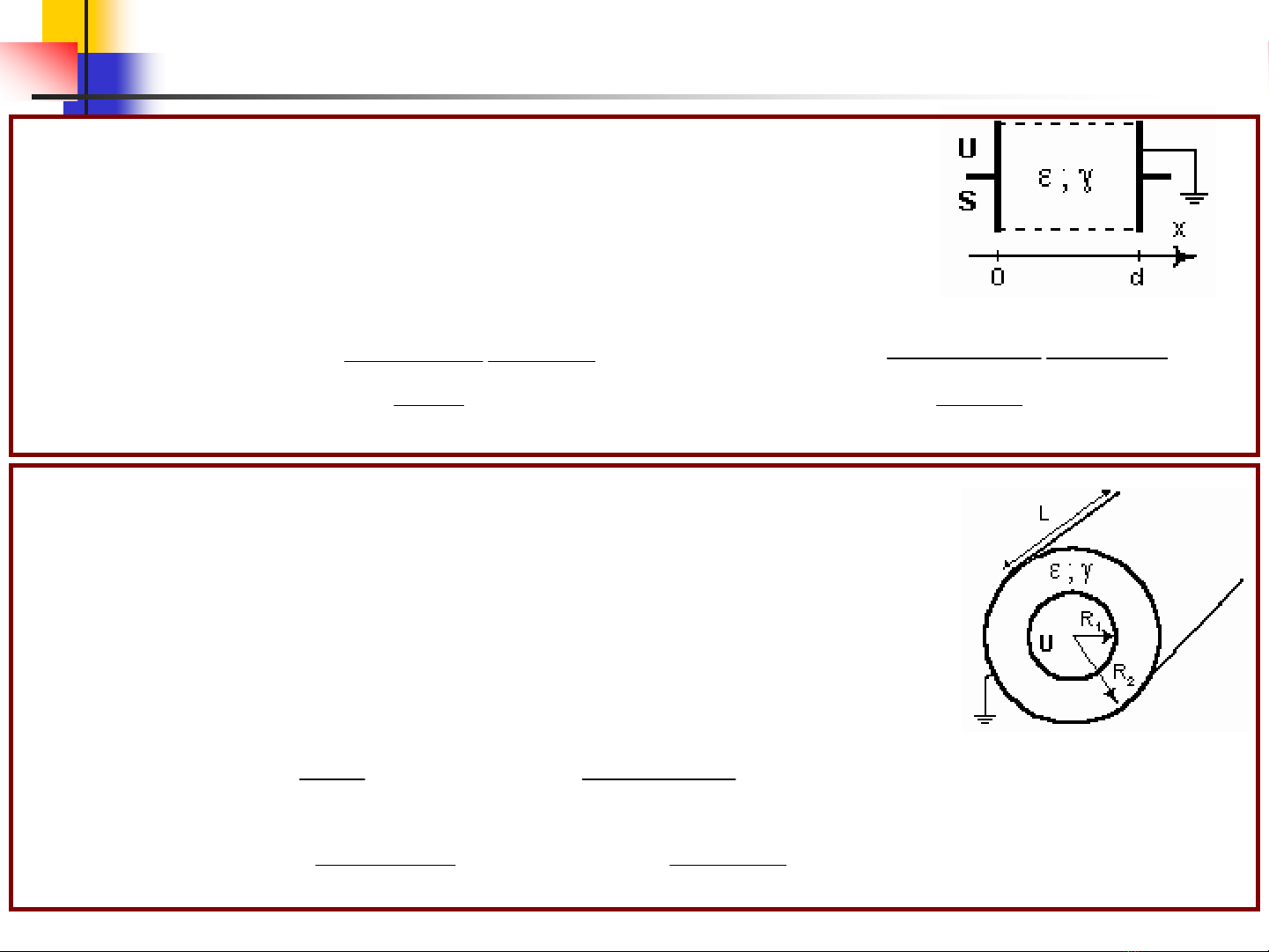
  3. BAØI TẬP CHƯƠNG 3 3.5: Tuï phaúng , dieän tích coát tuï S, khoaûng caùch d, hieäu theá U, ñieän moâi thöïc , ε = ε0.(a + bx) ; γ = γ0.(a + bx) , (γ0, a, b = const) , tìm : a) Vectô cöôøng ñoä tröôøng ñieän ? b) Maät ñoä khoái ñieän tích töï do vaø lieân keát ? → bU 1 → −b2ε 0 U 1 (ÑS: a) E = i x b) ρ = 0 ; ρlk = 2 )  a+bd  ( a + bx )  a + bd  ( a + bx ) ln   ln    a   a  3.6: Caùp ñoàng truïc , baùn kính loõi R1 = 1 cm, voû R2 = 4 cm, chieàu daøi L, hieäu theá U = 1 kV, ñieän moâi thöïc , coù ε = 4ε0 ; γ = k.r , vôùi k = 10-10 (S/cm2) , tìm : → → a) E , D , ρ , ρ trong ñieän moâi ? lk b) Doøng roø I0 treân ñôn vò daøi ? →1333 → → 471,9.10−12 → (ÑS: a) E = 2 i r (V / cm); D = i r (C / cm 2 ) b) ) Iro = 0,84 (µ A/ cm) 2 r r −12 −12 471,9.10 354.10 ρ =− (C / cm3 ) ; ρlk = (C / cm3 ) r3 r3 Problem_ch3 3
  4. BAØI TẬP CHƯƠNG 3 3.7 : Cho phieán daãn coù hình 1/4 vaønh khaên, tieát dieän chöõ nhaät , ñoä daøy laø h, ñoä daãn ñieän : γ = k/r, (k = const) , hieäu theá ñieän giöõa 2 ñieän cöïc 1 vaø 2 laø U . Tìm : a) Cöôøng ñoä doøng ñieän I ? b) Maät ñoä coâng suaát tieâu taùn trung bình theo theå tích ? AÙp duïng : a = 8 mm; b = 10 mm; h = 0,3 mm; k = 5600 S; vaø U = 10 V. 2hkU  1 1  (ÑS: a) I = π  -  = 267, 4 ( A) a b b) p J = 1 ∫ p J dV = 4 2kU 2  1 1  )  −  = 3,15.10 (W / m ) 11 3 V π (b -a ) π  a b  2 2 Problem_ch3 4
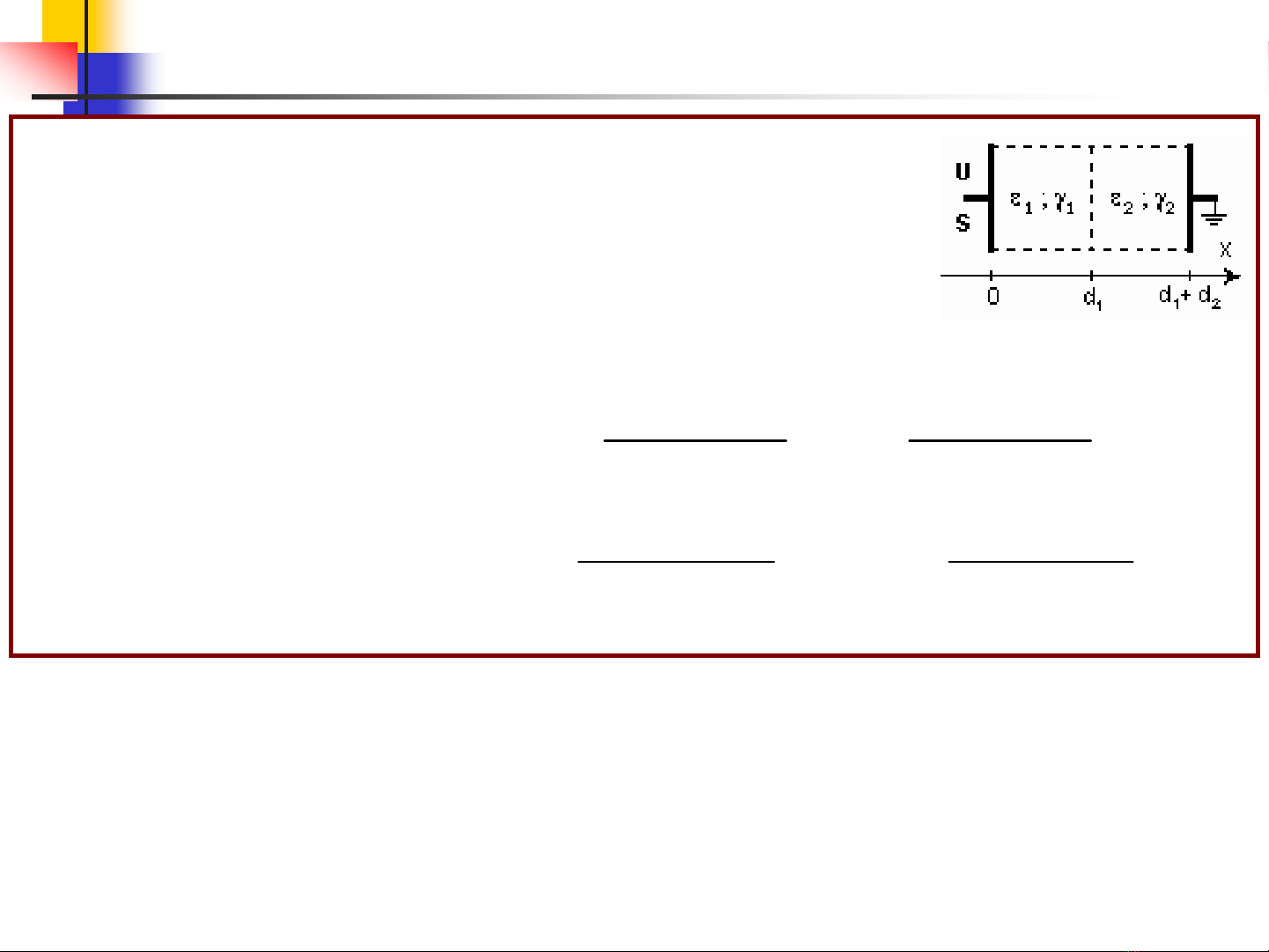
  5. BAØI TẬP CHƯƠNG 3 3.8 : Tuï phaúng , dieän tích coát tuï S, hieäu theá U, laáp ñaày 2 lôùp ñieän moâi thöïc (ε1, γ1) , (ε2, γ2) , vôùi ε1, ε2, γ1, γ2 = const , boû qua hieäu öùng meùp, tìm : a) Hieäu theá ñieän treân moãi lôùp ñieän moâi ? b) Maät ñoä ñieän tích maët töï do treân maët phaân caùch ñmoâi ? c) Ñieän trôû caùch ñieän cuûa tuï ? d1 γ 2 U d 2 γ1 U (ÑS: a) U1 = ; U2 = (d1 γ 2 +d 2 γ1 ) (d1 γ 2 +d 2 γ1 ) (ε 2 γ1 -ε1γ2 )U (d1γ2 +d2 γ1 ) b) σ = c) Rcd = ) (d1γ2 +d2 γ1 ) γ1γ2S Problem_ch3 5
  6. BAØI TẬP CHƯƠNG 3 3.9: Tuï ñieän truï , daøi L, goàm 2 lôùp ñieän moâi thöïc , coù ε1 ,ε2 ,γ1 , γ2 = const , tìm : → → a) J , E trong caùc lôùp ñieän moâi ? b) Theá ñieän trong moãi lôùp ñieän moâi ? c) Hieäu theá ñieän treân moãi lôùp ñieän moâi ? d) Ñieän trôû caùch ñieän cuûa tuï ? → → γ 1γ 2 U 1→ → γ 2U 1→ → γ 1U 1→ (ÑS: a) J 1 = J 2 = i r ; E1 = i r ; E2 = ir  c b r  c b r  c b r  γ 2 ln + γ 1 ln   γ 2 ln + γ 1 ln   γ 2 ln + γ 1 ln   a c  a c  a c γ 1U b b) ϕ 2 = ln  c b r γ  2 ln + γ 1 ln   a c  c b γ  2 ln + γ ln  γ 1U b  a 1 c c) U 2 = ln d) Rcd = )  c b c 2π Lγ 1γ 2 γ  2 ln + γ 1 ln   a c Problem_ch3 6
  7. BAØI TẬP CHƯƠNG 3 3.10: Tuï ñieän truï , baùn kính coát trong R1 vaø coát ngoaøi R2, chieàu daøi L, ñaët döôùi hieäu theá ñieän U, ñieän moâi thöïc , coù γ = γ0 = const , ε = ε0(R2/r) , tìm : ñieän trôû caùch ñieän, maät ñoä coâng suaát tieâu taùn, maät ñoä ñieän tích töï do vaø lieân keát (ρ, ρlk) trong ñieän moâi ? (ÑS: R cd = 1 ln R2 γ U 2 ; p tt = 2 2 0 2πγ 0 L R 1 r ln (R 2 /R 1 ) εR U ρ =− 3 0 2 ; ρlk =−ρ ) r ln(R 2 /R 1 ) Problem_ch3 7
  8. BAØI TẬP CHƯƠNG 3 3.11: Tuï ñieän caàu , baùn kính coát trong a = 1 cm, baùn kính coát ngoaøi b = 5 cm, giöõa 2 coát tuï laø ñieän moâi thöïc coù γ = k/r , vôùi k = 10-4 S. Doøng ñieän roø chaûy qua ñieän moâi coù cöôøng ñoä I = 0,2 A, tìm : a) Phaân boá theá ñieän trong ñieän moâi ? b) Hieäu theá ñieän U giöõa 2 coát tuï ? c) Ñieän daãn roø cuûa tuï ? 5.10−2 (ÑS: a) ϕ = 159ln b) 256,15 V c) 7,81.10-4 S ) r 3.12: Ñieän cöïc noái ñaát hình baùn caàu , baùn kính a. Doøng ñieän chaïy vaøo ñieän cöïc coù I = 105 A. Ñoä daãn ñieän cuûa ñaát γ = 5.10-2 (S/m). Tìm : a) Baùn kính a cuûa baùn caàu ñeå ñieän aùp böôùc (UAB) cöïc ñaïi coù Umax ≤ 50 V (ñoä daøi böôùc chaân AB = 0,8 m) ? b) Tính ñieän trôû noái ñaát öùng vôùi caâu a) ? → I 1→ (ÑS: a) E = i r ⇒ U AB ≤ U max ⇒ a ≥ 1,95 m 2πγ r 2 b) 1, 63 Ω ) Problem_ch3 8
  9. BAØI TẬP CHƯƠNG 3 3.13: Tính vectô caûm öùng töø taïi O bieát µ = µ0 ? → µ0I → (ÑS: B = (2 + π ) i z ) 4π a 3.14: Tính vectô caûm öùng töø taïi O ? ( bieát µ = µ0 ; R = 5 cm I = 10 A ; α = 2π/3 ) (ÑS: a) B = 8π 10−5 i z (T ) → → 3 → b) B = 0 ) Problem_ch3 9
  10. BAØI TẬP CHƯƠNG 3 3.15: Loõi caùp laø truï ñaëc , baùn kính a, mang doøng I phaân boá ñeàu theo tieát dieän , vaø voû truï , baùn kính b , mang doøng –I phaân boá ñeàu theo chu vi voû. Tính vectô caûm öùng töø taïi caùc mieàn ? ( bieát µ = ñoä thaåm töø cuûa loõi ) → µ Ir → µ0 I → (ÑS: B = i φ [r < a] ; i φ [ a < r < b]; 0 [r > b] ) 2π a 2 2π r 3.16: Loõi truï ñaëc , daøi voâ haïn, baùn kính a = 2 mm, mang doøng vôùi vectô maät ñoä khoái : → → J = 6.r. i z (A/m2 ) ( r: baùn kính höôùng truïc) a) Tìm vectô cöôøng ñoä tröôøng töø beân trong vaø ngoaøi loõi ? → b) Tính rot H ôû caû 2 mieàn ? → → 2a 3 → (ÑS: a) H = 2r i φ [r < a ]; 2 i φ [r > a] ) r Problem_ch3 10
  11. BAØI TẬP CHƯƠNG 3 → → 3.17: Doøng ñieän phaân boá khoâng ñeàu vôùi maät ñoä doøng J = J 0 e r-a vôùi J0 = const iz theo thieát dieän troøn baùn kính a cuûa vaät daãn ñaëc hình truï raát daøi vaø chaûy veà theo höôùng ngöôïc laïi treân moät maët truï daãn baùn kính b (b > a) , ñoàng truïc vôùi hình truï daãn ñaëc. Xaùc ñònh phaân boá cuûa cöôøng ñoä tröôøng töø trong töøng mieàn ? J 0e−a → → (ÑS: rb: H=0 ) Problem_ch3 11
  12. BAØI TẬP CHƯƠNG 3 3.18: Moâi tröôøng µ = µ0 vaø vectô maät ñoä 0 0
  13. BAØI TẬP CHƯƠNG 3 3.20*: Caùp ñoàng truïc, baùn kính loõi laø a, baùn kính trong cuûa voû laø c. Giöõa loõi vaø voû laø 2 lôùp töø moâi (coù ñoä daãn ñieän baèng 0) , tieáp giaùp nhau theo maët truï baùn kính b . Ñoä thaåm töø lôùp thöù nhaát (a < r < b) laø µ1 = const , ñoä thaåm töø lôùp thöù hai (b < r < c) laø µ2 = const. Doøng ñieän chaïy trong loõi vaø voû cuøng cöôøng ñoä I nhöng ngöôïc chieàu. a) Tìm vectô caûm öùng töø, theá vectô trong moãi lôùp töø moâi ? (Choïn theá vectô baèng 0 treân beà maët loõi) . b) Tính NL tröôøng töø , ñieän caûm treân ñôn vò daøi cuûa caùp ? (Boû qua phaàn naêng löôïng trong loõi vaø voû) .  µ 1I  µ 1I a B = A = ln (ÑS: a)  B = B i φ → →  1 2π r  1 2π r →   →  A = A i z B = µ 2I  A = µ 2 I ln b − µ 1 I ln b  2 2π r  2 2π r 2π a b)  2 I  b c   W = µ  1 ln + µ ln  4π  m0 2  a b    L = 1  µ ln b + µ ln c   0  1  ) 2π  2 a b  Problem_ch3 13
  14. BAØI TẬP CHƯƠNG 3 3.21: Tìm Φm gôûi qua 1 m chieàu daøi ñöôøng daây ñieän thoaïi do doøng ñieän I = 100 A taïo ra ? (bieát µ = µ0 ) (ÑS: 4,7 (µWb) ) 3.22: Tìm hoã caûm M giöõa 2 daây daãn mang doøng I ngöôïc chieàu vaø khung daây N voøng ? Tìm sññ caûm öùng u(t) neáu I = Imcos(ωt) ? (bieát µ = µ0 ) (ÑS: M = µ0 Nb ln d+a π d-a u (t ) = ω MI m sin(ω t ) ) Problem_ch3 14
  15. BAØI TẬP CHƯƠNG 3 3.23: Caùp ñoàng truïc, baùn kính loõi laø a, baùn kính voû laø b. Giöõa loõi vaø voû laø lôùp ñieän moâi ñoàng nhaát (γ = 0, ε = const, µ = const) . Hieäu theá ñieän giöõa loõi vaø voû laø U, doøng ñieän chaïy trong caùp coù cöôøng ñoä I. Tìm: a) Ñieän dung C0 , ñieän caûm L0 cuûa 1 m caùp ? b) Coâng suaát ñieän töø truyeàn qua tieát dieän (a < r < b) cuûa caùp ñoàng truïc ? 2πε µ (ÑS: a) C0 = ; L0 = ln(b/a) b) P=UI ) ln(b/a) 2π 3.24: Hai maët truï ñoàng truïc , kích thöôùc nhö hình veõ, mang doøng I ngöôïc chieàu. Tìm : a) Naêng löôïng tröôøng töø , ñieän caûm treân ñôn vò daøi ? b) Löïc töø taùc duïng leân ñôn vò daøi maët truï ngoaøi ? 2 (ÑS: a) W = µI b µ b m0 ln ; L 0 = ln 4π a 2π a 2 µI b) Fb = >0 ) 4π b Problem_ch3 15
  16. BAØI TẬP CHƯƠNG 3 3.25*: OÁng truï 2 lôùp kim loaïi : γ1 = 30.106 (S/m) , γ2 = 57.106 (S/m) , ñoàng truïc vôùi : a = 3 mm, b = 6 mm , c = 9 mm . Tìm cöôøng ñoä tröôøng töø trong caùc mieàn ? (HD: Coù J1, J2 = const vaø J1/γ1 = J2/γ2 ) (ÑS: 0 < r < a: H1 = 0  a 2  A a < r < b: H 2 = 28, 45.10  r − 4 ( )  r  m [7, 68 + 53, 75.104 (r 2 − b 2 )] A b < r < c: H 3 = ( ) r m 31,83 A c < r: H 4 = ( ) ) r m Problem_ch3 16
  17. BAØI TẬP CHƯƠNG 3 3.26*: Cho oáng truï vaø maët truï ñoàng truïc daøi voâ haïn, ñieän moâi giöõa oáng truï vaø maët truï coù ñoä thaåm töø µ0 , oáng truï coù ñoä thaåm töø µ0µr. Doøng ñieän khoâng ñoåi cöôøng ñoä I chaïy ngöôïc chieàu treân oáng truï vaø maët truï vaø phaân boá ñeàu . Tìm : a) Cöôøng ñoä tröôøng töø trong toaøn khoâng gian ? b) Naêng löôïng tröôøng töø tích luõy trong oáng truï vaø trong ñieän moâi treân ñôn vò daøi ? c) Ñieän caûm trong vaø ngoaøi treân ñôn vò daøi ?  (ÑS: a)  0 0 < r < R1 & r > R 3 b)   I(r 2 -R 12 ) µ 0I2 R 3 H=  R1 < r < R 2 W 0_ng = ln π 4π 2 2  2 r(R 2 -R 1 ) R2  I  R2 < r < R3  2π r µ0 µr I2  R 24 -R 14 R2  W0_tr =  − R 1 (R 2 -R 1 ) + R 1 ln 2 2 2 4  ) 4π ( R -R2 2 1) 2 2  4 R 1  Problem_ch3 17
ADSENSE

CÓ THỂ BẠN MUỐN DOWNLOAD

THÔNG TIN
TRỢ GIÚP
HỖ TRỢ KHÁCH HÀNG
Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn

Giấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015 Copyright © 2022-2032 TaiLieu.VN. All rights reserved.

 

Đồng bộ tài khoản
9=>0