
1
1
© TS. Lng Hu Tun
!
!!
! "
#
##
# $ %
&
&&
& ' ()
*
**
* +, "- ./ 0 1/ /
2
© TS. Lng Hu Tun
*
**
*+,
+,+,
+, "-
"-"-
"- ./
././
./ 0
00
0 1/
1/1/
1/ /
//
/
2
22
2
34
3434
34 /".
/"./".
/".
2
22
2+".
+".+".
+".
5
55
5
!2
!2!2
!2+".
+".+".
+".
)
))
) /
//
/
#2
#2#2
#21
11
1 ./$
./$./$
./$ 6
66
6 "4
"4"4
"4 /
//
/ /".
/"./".
/". )
))
)
&2
&2&2
&21/
1/1/
1/ /
//
/
2
3
© TS. Lng Hu Tun
*
**
*+,
+,+,
+, "-
"-"-
"- ./
././
./ 0
00
0 1/
1/1/
1/ /
//
/
2
22
2
34
3434
34 /".
/"./".
/".
221 /$ "- 74 8
224 ./$ ) 9/
4
© TS. Lng Hu Tun
22
2222
221
11
1 /$
/$/$
/$ "-
"-"-
"- 74
7474
74 8
88
8
: /$ "- 74 () / $ 8
;<=/> / ? () @< /
A%7 ./ " ./
B/> / () < "/C () C/% )
B/> / < "/ 4 D "//> / /%
/4 ) " ./ "
B/> / () C/% C> "/C () )
B/> / <
+,
+,+,
+, "-
"-"-
"- ./
././
./ " ./
B/> / () C/% C> "/C () )
B/> / C/% C> "/γ E∞γ EF

3
5
© TS. Lng Hu Tun
22
2222
224
44
4 ./$
./$./$
./$
)
))
)
9/
9/9/
9/
4 ./$ ) ;
B 9/ : 74 C/% /> / C ;G;
B 4 ./$ ) H : 8 3 CI /".
A// /". H " 4 ./$ /
9/ J . 74 : K
9/ /> L : />
B 9/ M MKEF=1K≠F
B 9/ N MK≠F=1KEF
6
© TS. Lng Hu Tun
*
**
*+,
+,+,
+, "-
"-"-
"- ./
././
./ 0
00
0 1/
1/1/
1/ /
//
/
2
22
2
34
3434
34 /".
/"./".
/".
2
22
2+".
+".+".
+".
5
55
5
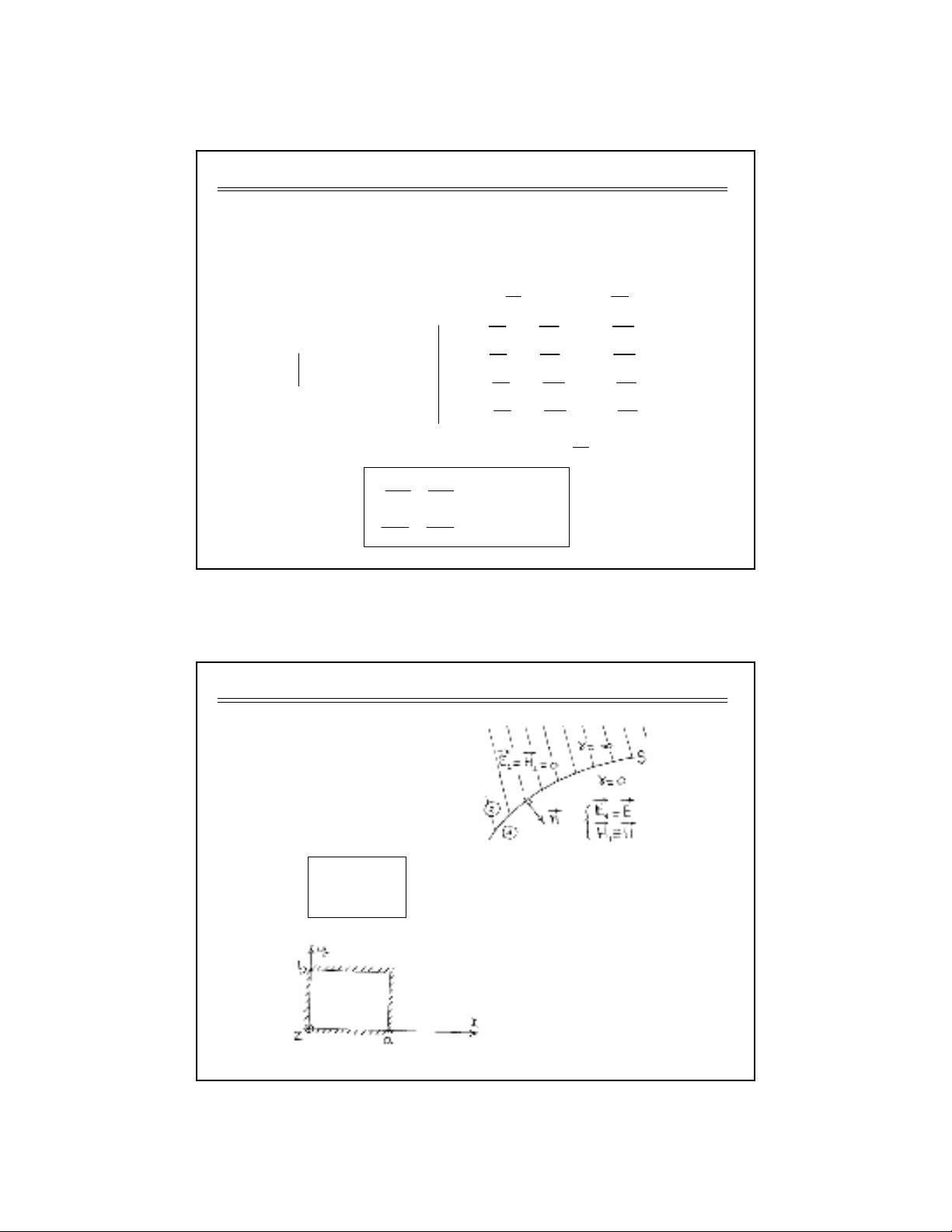
J . /". / $ " =4 " $ :=C/% /> /
?γ
E∞γ
EF@=$ % 4 /
22$ : 4 C %
229/ N
2!29/ M
2#2I $ /".
4
7
© TS. Lng Hu Tun
22
2222
22$
$$
$ :
::
:
C
CC
C %
%%
% ?@
?@?@
?@
$
$$
$ :
::
:
0 0
( , ) , ( , )
kz kz
E E x y e H H x y e
− −
= =
J . 74 : K2
A//". $ " % ./ H 74 / /
k j
β
= ±
rotH j E
ωε
=
rotE j H
ωµ
= −
2
1
( )
z z
c
E H
x
x y
K
E k j
ωµ
∂ ∂
∂ ∂
= − −
2
1
( )
z z
c
E H
y
y x
K
E k j
ωµ
∂ ∂
∂ ∂
= − +
2
1
( )
z z
c
H E
x
x y
K
H k j
ωε
∂ ∂
∂ ∂
= − +
2
1
( )
z z
c
H E
y
y x
K
H k j
ωε
∂ ∂
∂ ∂
= − −
2
2
2 2 2 2
c
v
K k
ω
ω µε β
= + = − +
2 2
2 2
2
0
z z
E E
c z
x y K E
∂ ∂
∂ ∂
+ + =
2 2
2 2
2
0
z z
H H
c z
x y K H
∂ ∂
∂ ∂
+ + =
... , ...
E H
z z
kE kH
∂ ∂
∂ ∂
= = − = = −
8
© TS. Lng Hu Tun
22
2222
22$
$$
$ :
::
:
C
CC
C %
%%
% ?@
?@?@
?@
4
44
4 C
CC
C %
%%
%
1 2
1 2
t t
n n
E E
B B
=
=
0
0
t
n
E
B
=
=
( ,0, ) 0
z
E x z
=

5
9
© TS. Lng Hu Tun
22
2222
229/
9/9/
9/
N?@
N?@N?@
N?@
0 :
z
H
=
2 2
2 2
2
0
z z
E E
c z
x y K E
∂ ∂
∂ ∂
+ + =
( ). ( ). ( . .)
kz
z
E X x Y y e s v
−
=
2 2
2 2
2
0
kz kz kz
d X d Y
c
dx dy
Ye Xe K XYe
− − −
+ + =
2 2
2 2
2
1 1
0
d X d Y
c
X Y
dx dy K
+ + =
2
2
2
2
2
1
2
1
sin( )
sin( )
d X
Xdx
d Y
Ydy
MX A Mx
Y B Ny
N
ϕ
ψ
= −
= +
= +
= −
2 2 2
c
K M N
= +
sin( ) sin( )
kz
z
E C Mx Ny e
ϕ ψ
−
= + +
( 0) 0
( 0) 0
( ) 0
( ) 0
z
z
z
z
E x
E y
E x a
E y b
= =
= =
= =
= =
0
0
Ma m
Nb n
ϕ
ψ
π
π
=
=
=
=
10
© TS. Lng Hu Tun
22
2222
229/
9/9/
9/
N?@
N?@N?@
N?@
sin sin n y
kz
m x
za b
E C e
π
π
−
=
2 2
1( )
z z z
c c
E H E
k
x
x y x
K K
E k j
ωµ
∂ ∂ ∂
−
∂ ∂ ∂
= − − =
2 2
1( )
z z z
c c
E H E
k
y
y x y
K K
E k j
ωµ
∂ ∂ ∂
−
∂ ∂ ∂
= − + =
2 2
1( )
z z z
c c
H E E
j
x
x y y
K K
H k j
ωε
ωε
∂ ∂ ∂
∂ ∂ ∂
= − + =
2 2
1( )
z z z
c c
H E E
j
y
y x x
K K
H k j
ωε
ωε
∂ ∂ ∂
−
∂ ∂ ∂
= − − =



![Tài liệu ôn tập Điện trường [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250709/linhnhil/135x160/31651752026408.jpg)
![Bài giảng Vật lý 1 và thí nghiệm: Chương 13 - Học viện Công nghệ Bưu Chính [Tài liệu chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250529/hatrongkim0609/135x160/17911750834556.jpg)






![Bộ câu hỏi lý thuyết Vật lý đại cương 2 [chuẩn nhất/mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251003/kimphuong1001/135x160/74511759476041.jpg)
![Bài giảng Vật lý đại cương Chương 4 Học viện Kỹ thuật mật mã [Chuẩn SEO]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250925/kimphuong1001/135x160/46461758790667.jpg)













