Bài giảng Bao phủ mạng không dây: Chương 3 - Bài toán Q-coverage và Q-connectivity trong mạng cảm biến không dây

Chia sẻ: _ _ | Ngày: | Loại File: PDF | Số trang:53

Thêm vào BST

Báo xấu

21
lượt xem 5
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bài giảng "Bao phủ mạng không dây: Chương 3 - Bài toán Q-coverage và Q-connectivity trong mạng cảm biến không dây" được biên soạn với các nội dung chính sau: Giới thiệu bài toán Q-coverage và Q-connectivity; Các nghiên cứu liên quan; Mô hình bài toán Q-coverage và Q-connectivity;... Mời các bạn cùng tham khảo bài giảng!

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng Bao phủ mạng không dây: Chương 3 - Bài toán Q-coverage và Q-connectivity trong mạng cảm biến không dây

Nội dung 1 Tổng quan 2 Bài toán K-coverage trong mạng cảm biến không dây 3 Bài toán Q-coverage và Q-connectivity trong mạng cảm biến không dây Giới thiệu bài toán Các nghiên cứu liên quan Mô hình bài toán Giải thuật đề xuất Thực nghiệm 4 Bài toán tối ưu thời gian bao phủ của mạng cảm biến 75 / 152
Bài toán Q-coverage Bài toán tổng quát hơn của bài K-coverage: mỗi mục tiêu có độ quan trọng khác nhau. 76 / 152
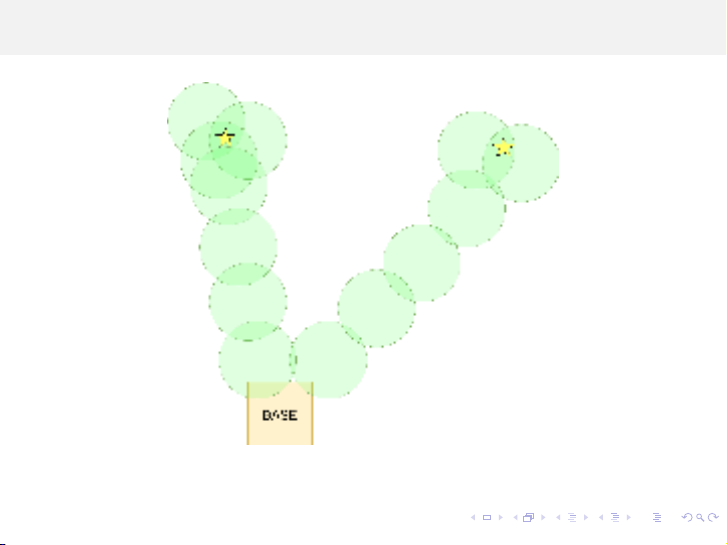
Bài toán Q-coverage Hình 31: Mô hình mạng cảm biến Q-coverage 77 / 152
Bài toán Q-connectivity Trong bài Q-coverage, mục tiêu được theo dõi bởi nhiều cảm biến, nhưng có thể chỉ có 1 đường kết nối đến trạm cơ sở. Nếu một nút bất kỳ trên đường truyền bị chết, kết nối giữa mục tiêu và trạm cơ sở sẽ không còn Để mạng thực sự có khả năng chịu lỗi, cần xây dựng nhiều đường đi hơn từ mục tiêu về trạm cơ sở. Nhận xét: Nếu mạng cảm biến là Q-connectivity, mạng cũng là Q-coverage. 78 / 152
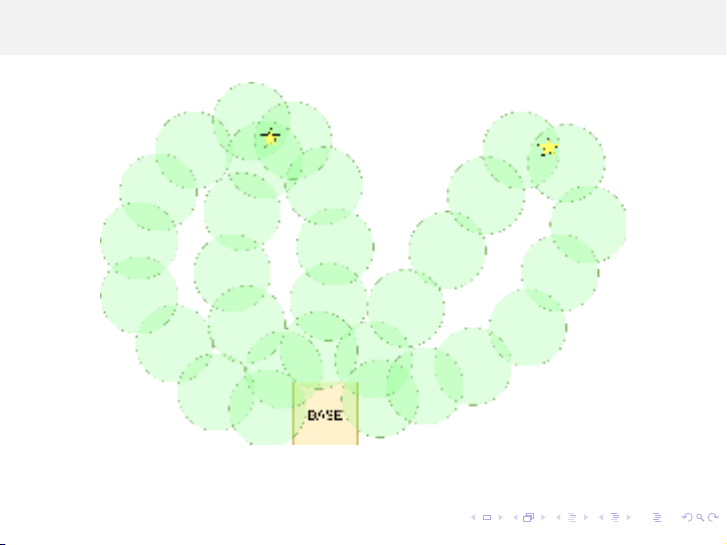
Bài toán Q-connectivity Hình 32: Mô hình mạng cảm biến Q-coverage kết hợp với Q-connectivity 79 / 152
Các nghiên cứu liên quan Trong nghiên cứu4 , tác giả đã trình bày: Phát biểu và mô hình hóa Q-coverage trong mạng cảm biến không dây Đề xuất thuật toán heuristic để giải quyết bài toán lập lịch cho các cảm biến từ tập n cảm biến và m mục tiêu cho trước để tối đa hóa thời gian sống của mạng và thoả mãn Q-coverage. 4 Manju Chaudhary, Arun K. Pujari, "Q-Coverage Problem in Wireless Sensor Networks", In Proceedings of the 10th International Conference on Distributed Computing and Networking, 2009. 80 / 152
Các nghiên cứu liên quan Trong bài báo5 , tác giả mô hình hóa bài toán lập lịch cho các cảm biến để tối đa hóa thời gian sống của mạng và thoả mãn Q-coverage. 5 Alok Singha, André Rossib, Marc Sevauxb, "Matheuristic approaches for Q-coverage problem versions in wireless sensor networks", Engineering Optimization, vol. 45, no. 5, pp. 609-626, Apr 2012. 81 / 152
Các nghiên cứu liên quan Trong nghiên cứu6 , tác giả đã xem xet các vấn đề: Triển khai sensor cho 1, k, q − coverage. Lên lịch bật tắt cho các cụm sensor. Tuy nhiên, phần triển khai còn đơn giản. 6 S. Mini, S. K. Udgata and S. L. Sabat, "Sensor Deployment and Scheduling for Target Coverage Problem in Wireless Sensor Networks", in IEEE Sensors Journal, vol. 14, no. 3, pp. 636-644, March 2014. 82 / 152
Nhận xét Các nghiên cứu kể trên có đặc điểm chung: Giải quyết bài toán lập lịch cho một số cảm biến đã được triển khai từ trước. Chưa quan tâm đến vấn đề kết nối. Đề xuất: Tự triển khai các sensor. Quan tâm đến vấn đề kết nối 83 / 152
Mô hình bài toán Cho miền cần theo dõi có kích thước WxH. B = (Bx , By ) là tọa độ của trạm cơ sở. T = {t1 , t2 , · · · , tNT } là tập mục tiêu cần theo dõi, với ti = (xi , yi ) là vị trí của mục tiêu ti . Q = {q1 , q2 , · · · , qNT } với qi là mức độ quan trọng của mục tiêu ti . Rs là bán kính cảm nhận của các cảm biến. Rc là bán kính truyền của các cảm biến. Yêu cầu: Tìm cách triển khai các cảm biến và nút chuyển tiếp sao cho mỗi mục tiêu ti có tối thiểu qi kết nối phân biệt (không chung bất kỳ nút trong nào) đến trạm cơ sở và tổng số cảm biến và nút chuyển tiếp được sử dụng là nhỏ nhất. 84 / 152
Giải thuật đề xuất Để giải quyết bài toán, ta chia bài toán thành 2 pha: Pha I: Triển khai các cảm biến để tạo thành mạng Q-coverage. Pha II: Từ các cảm biến đã triển khai, xây dựng Q-connectivity từ các mục tiêu về trạm cơ sở. 85 / 152
Giải thuật đề xuất Hình 33: Pha I: Triển khai Q-coverage 86 / 152
Giải thuật đề xuất Hình 34: Pha II: Xây dựng Q-connectivity 87 / 152
Pha I: Triển khai Q-coverage Cho miền cần theo dõi có kích thước WxH. T = {t1 , t2 , · · · , tNT } là tập mục tiêu cần theo dõi, với ti = (xi , yi ) là vị trí của mục tiêu ti . Q = {q1 , q2 , · · · , qNT } với qi là mức độ quan trọng của mục tiêu ti . Rs là bán kính cảm nhận của các cảm biến. Yêu cầu: Tìm cách triển khai các cảm biến sao cho mỗi mục tiêu ti được bao phủ bởi tối thiểu qi cảm biến và số cảm biến được sử dụng là nhỏ nhất. 88 / 152
Giải thuật đề xuất Nhận xét: Nếu có một lời giải tối ưu, ta luôn thu được một lời giải tối ưu khác bằng cách dịch chuyển các cảm biến sao cho có 2 mục tiêu nằm trên giới hạn phủ của cảm biến đó, trừ khi cảm biến bao phủ duy nhất một mục tiêu bị cô lập. Gọi các điểm khả thi Oij là các điểm mà targeti , targetj nằm trên đường tròn tâm Oij , bán kính Rs . Với mỗi cặp targeti và targetj sẽ có thể có 0 hoặc 1 hoặc 2 điểm khả thi. Nếu 1 mục tiêu không thể ghép cặp để tìm điểm khả thi thì ta sẽ tạo một điểm khả thi tại chính điểm đó. Ta chỉ xem xét việc đặt cảm biến tại các điểm khả thi. 89 / 152
Giải thuật đề xuất Hình 35: Tìm các điểm khả thi của 2 mục tiêu 90 / 152
Giải thuật đề xuất Giải thuật đề xuất cho pha I: Tìm các điểm khả thi để đặt cảm biến. Sử dụng mô hình Integer Linear Programming (ILP) để triển khai các cảm biến. Sử dụng thuật toán Angular Sweep Modified để triển khai các cảm biến. 91 / 152
Tìm các điểm khả thi Giải thuật để tìm các điểm khả thi: Với mỗi cặp mục tiêu (i, j), nếu khoảng cách giữa 2 mục tiêu không lớn hơn 2 × R, tìm các điểm khả thi như định nghĩa: tâm của đường tròn bán kính R sao cho targeti và targetj nằm trên đường tròn đó. Nếu một mục tiêu không thể ghép cặp thì tạo một khả thi tại chính điểm đó. Loại bớt các điểm khả thi có tập mục tiêu mà cảm biến đặt tại đó bao phủ là tập con của tập mục tiêu được bao phủ bởi cảm biến đặt tại một điểm khả thi khác. 92 / 152
Mô hình ILP là gì? Là bài toán tối ưu với hàm mục tiêu và ràng buộc tuyến tính. Bài toán ILP dưới dạng chuẩn: Maximize c T x thoả mãn Ax ≤ b (2) và x ≥ 0 Mọi bài toán ILP đều có thể đưa về dạng chuẩn. 93 / 152
Tại sao sử dụng ILP? Có thể mô hình hoá nhiều bài toán. Có nhiều thuật toán giải tổng quát. Có nhiều thư viện tối ưu, có khả năng: Giải tổng quát hoặc xem xét các cấu trúc đặc biệt của bài toán. Song song hoá. Giải chính xác, gần đúng (với sai số cho trước) hoặc dừng sớm (với thời gian chạy tối đa cho trước). 94 / 152