TS. Nguyeãn Thò Baûy - ÑHBK tp HCM -Baøi Giaûng CLC
THEÁ LÖU 1
CHÖÔNG
Doøng chaûy coù theá ⇔∃ϕ/thoaû ñ.k. (1) ⇔0
xyyx =
⎟
⎠
⎞
⎜
⎝
⎛
∂
ϕ∂
∂
∂
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
ϕ∂
∂
∂⇔0
y
u
x
ux
y=
∂
∂
−
∂
∂
⇔rot(u)=0
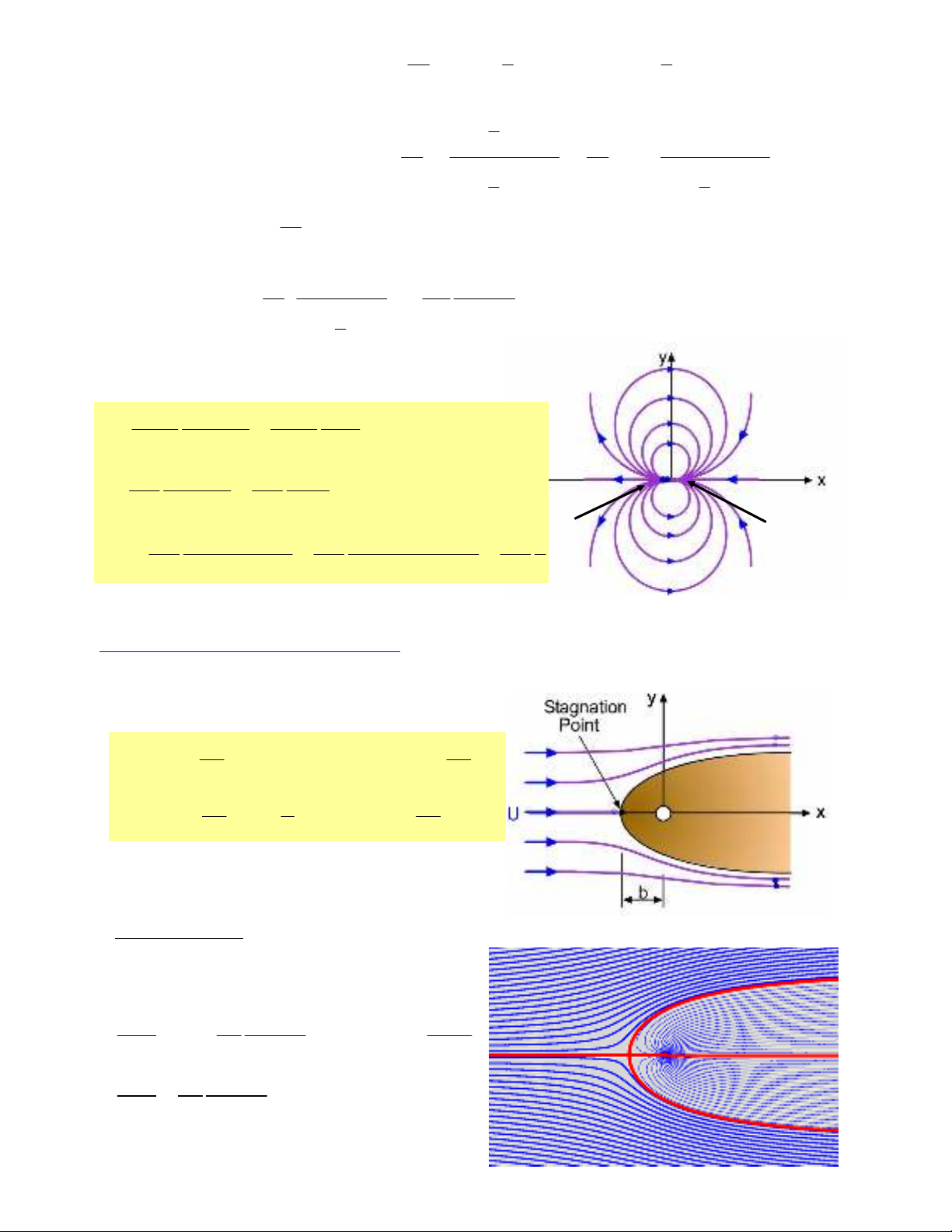
doøng chaûy phaúng, löu chaát lyù töôûng khoâng neùn ñöôïc chuyeån ñoäng oån ñònh
Giôùi haïn:
I. CAÙC KHAÙI NIEÄM CÔ BAÛN
1. Haøm theá vaän toác:
Ta ñònh nghóa haøm ϕsao cho: θ∂
ϕ∂
=
∂
ϕ
∂
=
∂
ϕ
∂
=
∂
ϕ
∂
=θr
1
u;
r
uhay
y
u;
x
uryx
Tröôøng veùctô u laø tröôøng coù theá khi: ∫
B
A
dsu
rchæ phuï thuoäc vaøo hai vò trí A vaø B.
Ta coù:
BA
B
A
B
A
B
A
)1(thoaûtoàntaïi
y
B
A
x
B
A
d
)dy
y
dx
x
(dsu)dyudxu(dsu
ϕ−ϕ=ϕ=
∂
ϕ∂
+
∂
ϕ∂
=+=
∫
∫∫
⇒
∫∫
ϕ
rr
chæ phuï thuoäc vaøo giaù trò haøm theá taïi A vaø B.
Roõ raøng töø chöùng minh treân, ∫
B
A
dsu
r
Vaäy:
(1)
A
B
n
u
un
us
0dyudxu0d yx
=
+
⇔
=
ϕ
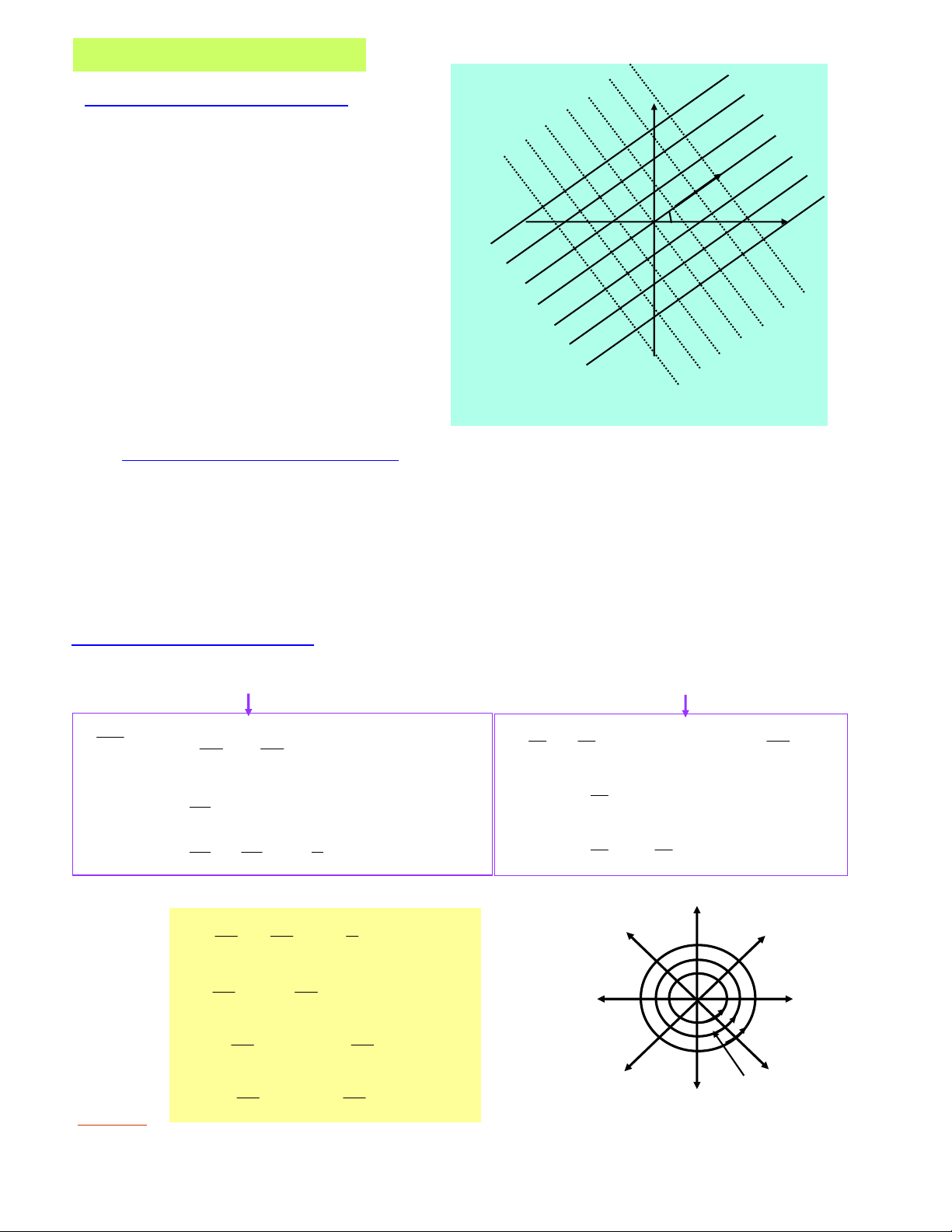
2. Phöông trình ñöôøng ñaúng theá:
3. YÙ nghóa haøm theá vaän toác: ABAB
−
ϕ
=
Γ∫
=Γ
B
A
sAB dsulaølöusoávaäntoác
4. Tính chaát haøm theá:
Töø ptr lieân tuïc, ta coù: 0
yx
0
yyxx
0
y
u
x
u
2
2
2
2
y
x=
∂
ϕ∂
+
∂
ϕ∂
⇔=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
ϕ∂
∂
∂
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
ϕ∂
∂
∂
⇔=
∂
∂
+
∂
∂
⇔Haøm theá thoaû phöông trình Laplace
TS. Nguyeãn Thò Baûy - ÑHBK tp HCM -Baøi Giaûng CLC
THEÁ LÖU 2
5. Haøm doøng:
Khi doøng chaûy löu chaát khoâng neùn ñöôïc toàn taïi, thì caùc thaønh phaàn vaän toác cuûa noù
thoaû ptr lieân tuïc :
r
u;
r
1
uhay
x
u;
y
u/0
y
u
x
uryx
y
x
∂
ψ∂
−=
θ∂
ψ∂
=
∂
ψ∂
−=
∂
ψ∂
=ψ∃⇔=
∂
∂
+
∂
∂
θ
ψgoïi laø haøm doøng. Nhö vaäy ψtoàn taïi trong moïi doøng chaûy,
coøn ϕchæ toàn taïi trong doøng chaûy theá.
6. Haøm doøng trong theá phaúng:
Vì laø doøng chaûy theá neân: 0
yx
0
yyxx
0
y
u
x
u
2
2
2
2
x
y=
∂
ψ∂
+
∂
ψ∂
⇔=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
ψ∂
∂
∂
−
⎟
⎠
⎞
⎜
⎝
⎛
∂
ψ∂
∂
∂
−⇔=
∂
∂
−
∂
∂
Vaäy trong doøng theá thì haøm ψthoaû ptr Laplace.
7. Ñöôøng doøng vaø ptr:
Töø ptr ñöôøng doøng: 0d0dx
x
dy
y
0dxudyuyx =ψ⇔=
∂
ψ
∂
+
∂
ψ
∂
⇔=−
x
y
O
n
nx
ny
dx
dy
ds
α
(-dx=ds.sinα)
Nhö vaäy treân cuøng moät ñöôøng doøng thì giaù trò ψlaø haèng soá.
8. YÙ nghóa haøm doøng:
Ta coù:
∫∫∫
∫∫∫∫
ψ−ψ=ψ=
∂
ψ∂
−
∂
ψ∂
=−=
α+α=+===
B
A
AB
B
A
B
A
yx
B
A
yx
B
A
yyxx
B
A
B
A
nAB
ddx
x
dy
y
dxudyu
dssinudscosudsnudsnudsnudsuq rr
Vaäy: ABAB
qψ−ψ=
9. Söï tröïc giao giöõa hoï caùc ñöôøng doøng vaø ñöôøng ñaúng theá:
0)u(u)u(u
yyxx xyyx =+−=
∂
ψ∂
∂
ϕ∂
+
∂
ψ∂
∂
ϕ∂
Suy ra hoï caùc ñöôøng doøng vaø caùc ñöôøng ñaúng theá tröïc giao vôùi nhau.
10. Coäng theá löu:
...
...
21
21
+ψ+ψ=ψ
+
ϕ
+
ϕ
=
ϕ
11. Bieãu dieãn doøng theá:
vôùi z = x+iy = eiα.
Theá phöùc f(z):
ψ
+
=i)z(
f
Nhö vaäy: dy
d
i
dx
d
iuu
dz
d
f
yx
ψ
+
ϕ
=−=
Ñeå bieåu dieãn doøng chaûy theá, ta coù theå bieãu dieãn rieâng töøng haøm doøng vaø haøm theá, ta
cuõng coù theå keát hôïp haøm doøng vôùi haøm theá thaønh moät haøm theá phöùc nhö sau::
TS. Nguyeãn Thò Baûy - ÑHBK tp HCM -Baøi Giaûng CLC
THEÁ LÖU 3
II. CAÙC VÍ DUÏ VEÀ THEÁ LÖU
x
O
y
ϕ=0
ϕ=1
ϕ=2
ϕ=3
ϕ=-1
ϕ=-2
ϕ=-3
ψ=0
ψ=1
ψ=2
ψ=3
ψ=-3
ψ=-2
ψ=-1
V0
α
1. Chuyeån ñoäng thaúng ñeàu:töø xa voâ
cöïc tôùi, hôïp vôùi phöông ngang moät goùc
α.
ux= V0cosα;u
y= V0sinα
dψ= uxdy - uydx
ψ= V0ycosα-V
0xsinα+ C
Choïn:ψ=0 laø ñöôøng qua goác toaï ñoä
⇒C=0.
Vaäy: ψ= V0ycosα-V
0xsinα
Töông töï: ϕ= V0xcosα+ V0ysinα
Bieãu dieãn baèng haøm theá phöùc:
F(z) = ϕ+iψ=(V
0xcosα+ V0ysinα) + i(V0ycosα-V
0xsinα)
= x(V0cosα-iV
0sinα)+yi(V0cosα-iV
0sinα)
= az
vôùi: a=(V0cosα-iV0sinα) laø soá phöùc; z=x+iy laø bieán phöùc.
2. Ñieåm nguoàn, ñieåm huùt: vôùi löu löôïng q taâm ñaët taïi goác toaï ñoä.
(q>0:ñieåm nguoàn; q<0:ñieåm huùt).
⇒Hoï caùc ñöôøng doøng laø nhöõng ñöôøng thaúng qua O.
)yxln(
4
q
)rln(
2
q
1rkhi0choïn;C)rln(
2
q
dr
r2
q
drudrudruddr
r
d
22
rr
+
π
=
π
=ϕ⇒
==ϕ+
π
=ϕ⇒
π
==θ+=θ
θ∂
ϕ
∂
+
∂
ϕ
∂
=ϕ θ
⎟
⎠
⎞
⎜
⎝
⎛
π
=θ
π
=ψ⇒
=θ=ψ+θ
π
=ψ⇒
θ=θ+−=θ
θ∂
ψ∂
+
∂
ψ∂
=ψ⇒
⎪
⎭
⎪
⎬
⎫
=
πθ
θ
x
y
arctg
2
q
2
q
0khi0choïn;C
2
q
drudrudruddr
r
d
0u r2
q
u
rr
r=
Haøm doøng: Haøm theá vaän toác:
⎪
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎪
⎨
⎧
=
π
=
π
=
+
π
=θ+
π
=
+
π
=
π
=ϕ
⎟
⎠
⎞
⎜
⎝
⎛
π
=θ
π
=ψ
θ
θ
zlnazln
2
q
)reln(
2
q
)elnr(ln
2
q
)ir(ln
2
q
)z(f
)yxln(
4
q
)rln(
2
q
x
y
arctg
2
q
2
q
i
i
22
Keát luaän: O
ϕ
ψ=0
ψ=(q/4)
ψ=q/2
ψ=3q/
4
Ghi chuù:
Tröôøng hôïp ñieåm nguoàn (huùt) coù taâm ñaët taïi moät vò trí khaùc goác toaï ñoä, ví duï ñaët taïi
A(x0; y0) thì trong coâng thöùc tính haøm doøng (hoaëc theá vaän toác), tai vò trí naøo coù caùc bieán x
phaûi thay baèng (x=x0) ; taïi vò trí naøo coù bieán y phaûi thay baèng (y-y0).
TS. Nguyeãn Thò Baûy - ÑHBK tp HCM -Baøi Giaûng CLC
THEÁ LÖU 4
3. Xoaùy töï do:ñaët taïi goác toaï ñoä vaø coù löu soá vaän toác ∫==Γ
C
constdsu
r
⎪
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎪
⎨
⎧
=
π
Γ−
=
π
Γ−
=
θ+
π
Γ
−=−θ
π
Γ
=
+
π
Γ−
=
π
Γ−
=ψ
⎟
⎠
⎞
⎜
⎝
⎛
π
Γ
=θ
π
Γ
=ϕ
⇒
⎪
⎩
⎪
⎨
⎧
=
π
Γ
=
=
θ
θ
zlnazln
2
i
)reln(
2
i
)ir(ln
2
i
)rlni(
2
)z(f
)yxln(
4
)rln(
2
x
y
arctg
22
const
r2
u
0u
i
22
r
O
ψ
ϕ=0
ϕ=Γ/4
ϕ= Γ/2
ϕ=3Γ/4
Γ>0: xoaùy döông
Ghi chuù:
Γ>0: xoaùy döông ngöôïc chieàu kim ñoàng hoà;
Γ<0: xoaùy aâm thuaän chieàu kim ñoàng hoà;
Töông töï, ta coù treân ñaây laø xoaùy ñaët taïi O(0,0).
Muoán bieãu dieãn cho xoaùy coù taâm ñaët taïi ñieåm
baát kyø, ta cuõng thöïc hieän nhö trong phaàn ghi
chuù cuûa ñieåm nguoàn, huùt.
4. Löôõng cöïc: laø caëp ñieåm nguoàn + huùt coù cuønglöulöôïngqñaëtcaùchnhaumoät
ñoaïn εvoââ cuøng nhoû (cho ε→0 vôùi ñieàu kieän εq→m0, laø moment löôõng cöïc).
Ví duï ta xeùt tröôøng hôïp naèm treân truïc hoaønh:
Tìmhaømdoøng:
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
+
ε
−
⎟
⎠
⎞
⎜
⎝
⎛ε
+−
⎟
⎠
⎞
⎜
⎝
⎛ε
−
π
=
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎛
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
ε
−
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
ε
+
+
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
ε
−
−
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
ε
+
π
=
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
ε
−
−
ε
+
π
=θ−θ
π
=ψ+ψ=ψ
2
2
2
hnhn
y
4
x
2
xy
2
xy
arctg
2
q
2
x
y
2
x
y
1
2
x
y
2
x
y
arctg
2
q
2
x
y
arctg
2
x
y
arctg
2
q
)(
2
q
Khi ε→0 töû soá trong daáu arctg tieán tôùi 0 neân ta coù theå vieát:
22
0
2
2
22
2
2yx
y
2
m
y
4
x
y
2
q
y
4
x
2
xy
2
xy
2
q
+
π
−
→
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
+
ε
−
ε−
π
=
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
+
ε
−
⎟
⎠
⎞
⎜
⎝
⎛ε
+−
⎟
⎠
⎞
⎜
⎝
⎛ε
−
π
=ψ
TS. Nguyeãn Thò Baûy - ÑHBK tp HCM -Baøi Giaûng CLC
THEÁ LÖU 5
+q -q
ψ
Tìmhaømtheávaäntoác:
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
+
⎟
⎠
⎞
⎜
⎝
⎛ε
−
ε
+
π
=
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
+
⎟
⎠
⎞
⎜
⎝
⎛ε
−
+
⎟
⎠
⎞
⎜
⎝
⎛ε
+
π
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛+
⎟
⎠
⎞
⎜
⎝
⎛ε
−−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛+
⎟
⎠
⎞
⎜
⎝
⎛ε
+
π
=ϕ+ϕ=ϕ
2
2
2
2
2
2
2
2
2
2
hn
y
2
x
x2
1ln
4
q
y
2
x
y
2
x
ln
4
q
y
2
xlny
2
xln
4
q
Trieån khai ...
2
x
x)x1ln( 2
+−=+ vaø boû qua caùc soá haïng baäc cao voâ cuøng beù, ta coù:
0khi
yx
x
2
m
y
2
x
x2
2
q
22
0
2
2→ε
+
π
→
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛ε
−
ε
π
=ϕ
Vaäy toùm laïi, ñoái vôùi chuyeån ñoäng löôõng cöïc thì:
z
1
2
m
)sini(cosr
sincos
2
m
r
sinicos
2
m
)z(f
r
cos
2
m
yx
x
2
m
r
sin
2
m
yx
y
2
m
0
22
00
0
22
0
0
22
0
π
=
θ+θ
θ+θ
π
=
θ−θ
π
=
θ
π
=
+
π
=ϕ
θ
π
−
=
+
π
−
=ψ
5. Doøng chaûy quanh nöûa coá theå:
Laø choàng nhaäp cuûa chuyeån ñoäng thaúng ñeàu ngang (U0)+ nguoàn taïi goác toaï ñoä (q)
θ
π
+θ=
π
+=ψ
π
+θ=+
π
+=ϕ
2
q
sinru)
x
y
(arctg
2
q
yu
rln
2
q
cosru)yxln(
4
q
xu
00
0
2
02
Ñieåm döøng A:
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=⇔=
+π
=
∂
ϕ∂
π
−=⇔=
+π
+=
∂
ϕ∂
⇔
==⇔=
⇑
0y0
yx
y2
4
q
y
u2
q
x0
yx
x2
4
q
u
x
0u;0u0u
A
22
0
A
22
0
yAxAA
A