Bài
giảng
Hình
học
vi
phân
của
Đường
và
Mặt
Huỳnh
Quang
Vũ
Bản
ngày
14
tháng 10
năm
2022
Bài giảng Hình học Vi phân của
Đường và Mặt
HuỳnhQuangVũBảnngày14tháng10năm2022Địachỉ:KhoaToán-TinhọcTrườngĐạihọcKhoahọcTựnhiênĐạihọcQuốcgiaThànhphốHồChíMinh.Email:hqvu@hcmus.edu.vn.Web:https://sites.google.com/view/hqvu/.TómtắtnộidungĐâylàbàigiảngmônMTH10480HìnhhọcViphân,mộtmônhọctựchọntrongchươngtrìnhđàotạotrìnhđộđạihọcngànhToánhọcởTrườngĐạihọcKhoahọcTựnhiênĐHQG-HCM,gồm15buổihọctrong15tuầntừtháng2tớitháng6năm2022.VìphảihọctrựctuyếndodịchCOVID-19nênlớphọcdùngbảngđiệntử,nhờđónhữngphầnđượcviếtvàvẽrađãlưulạiđược,sauđóphầnlớnđượcHồNguyễnHuyềnThư(sinhviênkhóa2017)đánhmáyởdạngLATEXvàchènhìnhvàotháng9năm2022.Mỗimụcởđâylàghichépcủamộtbuổihọc.Mục lục
1Độcongcủađường32Tínhtoánđộcong62.1Côngthứctínhđộcong........................62.2Dấucủađộcongcủađườngcongphẳng...............83Đườngcongvớiđộcongchotrước93.1Dấucủađộcongcủađườngcongphẳng:côngthứctính......93.2HệphươngtrìnhFrénet........................104Mặtchínhquy135Vídụmặtchínhquy151
2MỤCLỤC6Mặtphẳngtiếpxúc,ánhxạđạohàm206.1Mặtphẳngtiếpxúc..........................206.2Ánhxạđạohàm............................217Độcongcủamặt227.1Mặttrònxoay..............................237.2ÁnhxạGauss..............................248Độcongpháptuyến,độcongchính,tínhtoán278.1Độcongpháptuyến..........................278.2Độcongchính.............................288.3Tínhtoán................................299Vídụvềđộcong3010Đườngtrắcđịa3111Phươngtrìnhcủađườngtrắcđịa3311.1TínhcáchệsốChristoffel.......................3511.2Sựtồntạinghiệmcủahệphươngtrìnhđườngtrắcđịa.......3612TínhnộitạicủađộcongGauss,đẳngcấuhìnhhọc4012.1ĐộcongGausstínhtheomêtrícRiemann..............4012.2Đẳngcấuhìnhhọc...........................4113ĐịnhlýGauss–Bonnet4613.1Độcongtrắcđịa............................4813.2Dạngđịaphương............................4913.3Dạngtoàncục.............................5014Sơlượcmộtsốpháttriểntiếptheo5214.1Tínhchấttoàncụccủađườngtrắcđịa................5214.2Mởrộnglênmặt𝑛-chiềutrongkhônggian(𝑛+1)-chiều.....5214.3Mởrộnglênmặttrừutượng.....................5314.4Mặtphẳnghyperbolic.........................5415Đềtàinhóm5815.1Yêucầu.................................5815.2Danhsáchđềtài............................58
3Về môn học
Mônhọcnàynhằmcungcấpkiếnthứccơbảnvềhìnhhọcviphântrênmặthaichiều.Đâylànhữnghiểubiếtchungbổíchchobấtkìaihọctoán.Mộtsốvấnđềtrongmônhọctươngtácvớicácđềtàitronggiảitíchhàmnhiềubiến,đạisốtuyếntính,phươngtrìnhviphân,phéptínhbiếnphân,tôpô.Mônhọcgiúpngườihọcdễdànghơnkhigặpcáctiếpcậntrừutượngnếuđivàomộtsốlĩnhvựccủagiảitíchtoàncục,giảitíchhìnhhọc,phươngtrìnhđạohàmriêng,phươngtrìnhviphân,tôpô,vàhìnhhọc.PhầncuốicủamônhọchướngtớichongườihọctiếpxúcbanđầuvớihìnhhọcviphânnhiềuchiềutrênđatạpRiemann.NộidungchínhcủamônhọcgồmĐộcongcủađường;Độcongcủamặt;ĐịnhlýGaussvềtínhnộitạicủađộcong;Đườngtrắcđịa;ĐịnhlýGauss–Bonnet;ĐatạpRiemann;Hìnhhọchyperbolic2chiều.Ngườihọccầnnắmvữngphéptínhviphânhàmnhiềubiếnvànhữngkháiniệmbanđầuvềkhônggianmêtríc,sẵnsànglàmnhữnglýluậnvàtínhtoántoánhọc,nếucóhiểubiếtcơbảnvềtôpôsẽthuậnlợihơnchophầnsaucủamônhọc.GiáotrìnhchínhcủamônhọclàcuốnsáchcủadoCarmo[1].1 Độ cong của đường
Giốngnhưtrongtíchphânđường,đểnóivềtínhcongcủađườngtakhởiđầuvớiđườngđi(chuyểnđộng)thayvìconđường(tậpđiểm).Tínhcongcủaconđườngđượcphảnánhthôngquasựthayđổiphươngchuyểnđộngtrênđường(vàtínhthẳngđượcphảnánhquaviệcphươngchuyểnđộngkhôngđổi).Tuynhiêncónhiềuchuyểnđộngtrêncùngmộtconđường,vàsựthayđổiphươngchuyểnđộngcòncóthểphụthuộcvàocáchchuyểnđộng.Vậyđểtínhcongthuầntúyphảnánhthuộctínhcủaconđườngthìtacầnmộtcáchchuẩnhóa.Tachọnchuẩnhóabằngcáchxétcácchuyểnđộngvớitốcđộhằngbằng1.Mộtđườngđi(path)làmộtánhxạtừmộtkhoảngsốthực𝐼vàokhônggianEuclidℝ𝑛:𝛼∶𝐼→ℝ𝑛𝑡↦𝛼(𝑡).
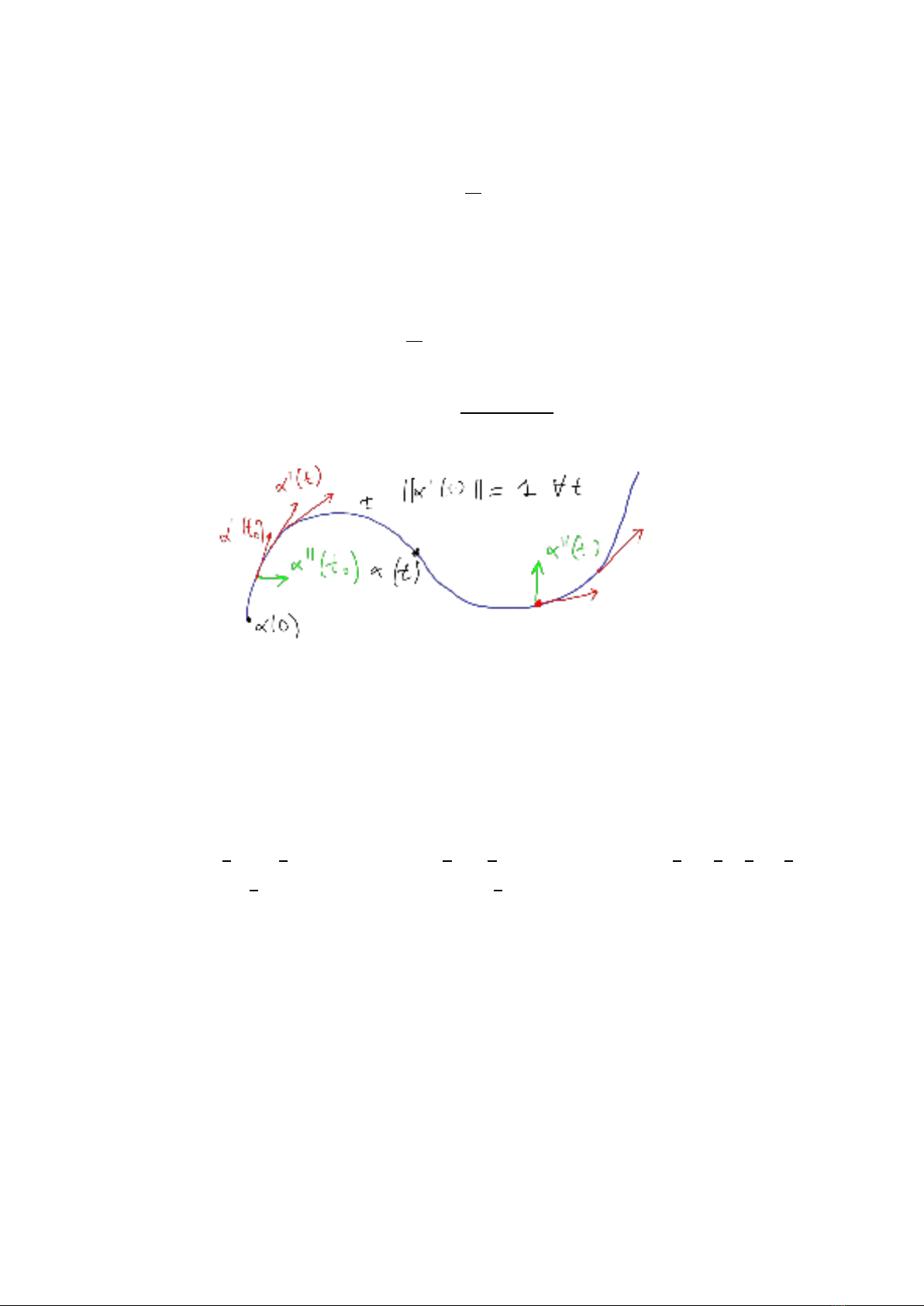
41ĐỘCONGCỦAĐƯỜNGVậntốccủađườngđi𝛼tạithờiđiểm𝑡là𝛼′(𝑡)=(𝑑𝑑𝑡𝛼)(𝑡)chỉhướngcủa𝛼tại𝑡.Tagiảthiết‖𝛼′(𝑡)‖=1,∀𝑡∈𝐼đểvectơ𝛼′(𝑡)thuầntúychỉhướngchuyểnđộng.Sựthayđổicủahướngtheothờigianđượcchobởivéctơgiatốc𝑑𝑑𝑡𝛼′(𝑡)=𝛼″(𝑡).𝛼″(𝑡0)=lim𝑡→𝑡0𝛼′(𝑡)−𝛼′(𝑡0)𝑡−𝑡0.Địnhnghĩa1.1.Vớigiảthiếtđường𝛼thỏa∀𝑡,‖𝛼′(𝑡)‖=1thìđộcongcủavếtcủađường𝛼tạiđiểm𝛼(𝑡)làsốthực𝑘(𝑡)=‖𝛼″(𝑡)‖.Vídụ1.2.Trênđườngthẳngtacóchuyểnđộng𝛼=𝑎+𝑡𝑣,với𝑎và𝑣làhằngvà𝑣làvectơđơnvịtrongℝ𝑛.Khiđó𝛼′(𝑡)=𝑣và𝛼″(𝑡)=0,vậyđộcongluônbằng0.Vídụ1.3.Trênđườngtròntâm0bánkính𝑅trongℝ2xétchuyểnđộng𝛼(𝑡)=(𝑅cos𝑡𝑅,𝑅sin𝑡𝑅).Tacó𝛼′(𝑡)=(−sin𝑡𝑅,cos𝑡𝑅),‖𝛼′(𝑡)‖=1,𝛼″(𝑡)=(−1𝑅cos𝑡𝑅,−1𝑅sin𝑡𝑅),‖𝛼″(𝑡)‖=1𝑅.Vậyđộcongtạimọiđiểmbằng1𝑅.Nhắclại[mônGiảitích3],chiềudàicủađườngđiđượcchobởitíchphântheothờigiancủatốcđộ:𝑠(𝑡)=∫𝑡𝑎‖𝛼′(𝑢)‖𝑑𝑢.Khitốcđộluônbằng1thìchiềudàiquãngđườngđiđược𝑠đúngbằngthờigianđi𝑡.Đườngđiđượcgọilàchínhquy(regular)nếuvậntốcluônkháckhông[1,tr.17].Mệnhđề1.4.Vớimọiđườngđichínhquytồntạiđườngđicócùngvếtmàcótốcđộluônbằng1.