1
Phần 1
HÌNH HỌA
2
Chương 1
Mơ đâu
Cơ sở của biểu diễn
3
1.1 Giới thiệu môn học
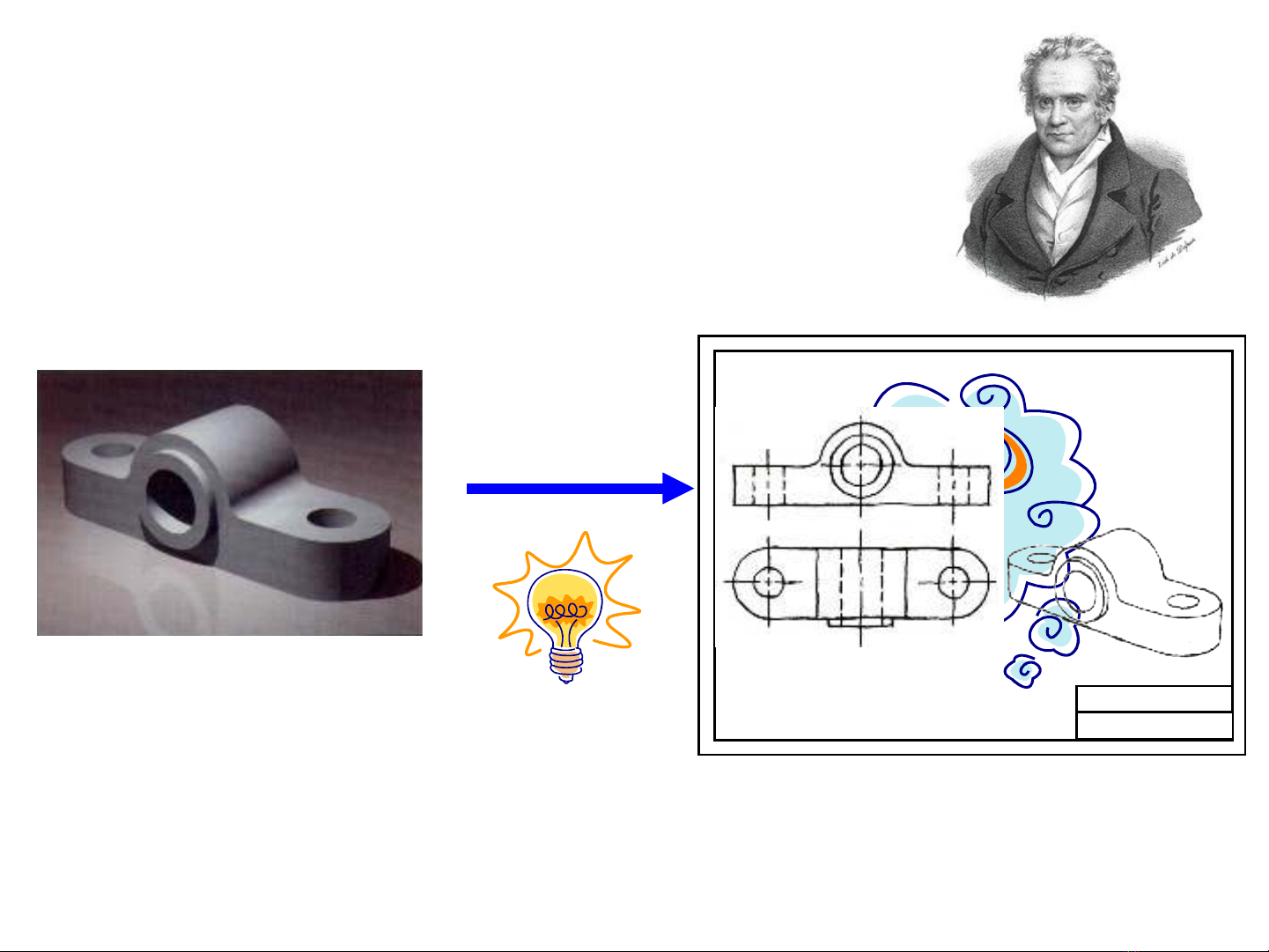
Trong ky thuât, ban ve ky thuât( trên giây) đươc sư dung
trong san xuât va$ trao đôi thông tin giưa cac nha$ thiêt kê.
Ban ve ky thuât la$ môt măt phăng 2 chiê$u co$n hâ$u hêt vât
thê đê$u la$ cac vât thê 3 chiê$u.
Vây la$m sao đê biêu diên cac đôi tương 3 chiê$u lên măt
phăng 2 chiê$u?
Hi$nh hoa
Gaspard Monge
Đối tượng môn học
- Nghiên cứu các phương pháp biểu diễn các hình không gian trên một mặt phẳng
- Nghiên cứu các phương pháp giải các bài toán không gian trên một mặt phẳng
4
1.2 - Phép chiếu xuyên tâm
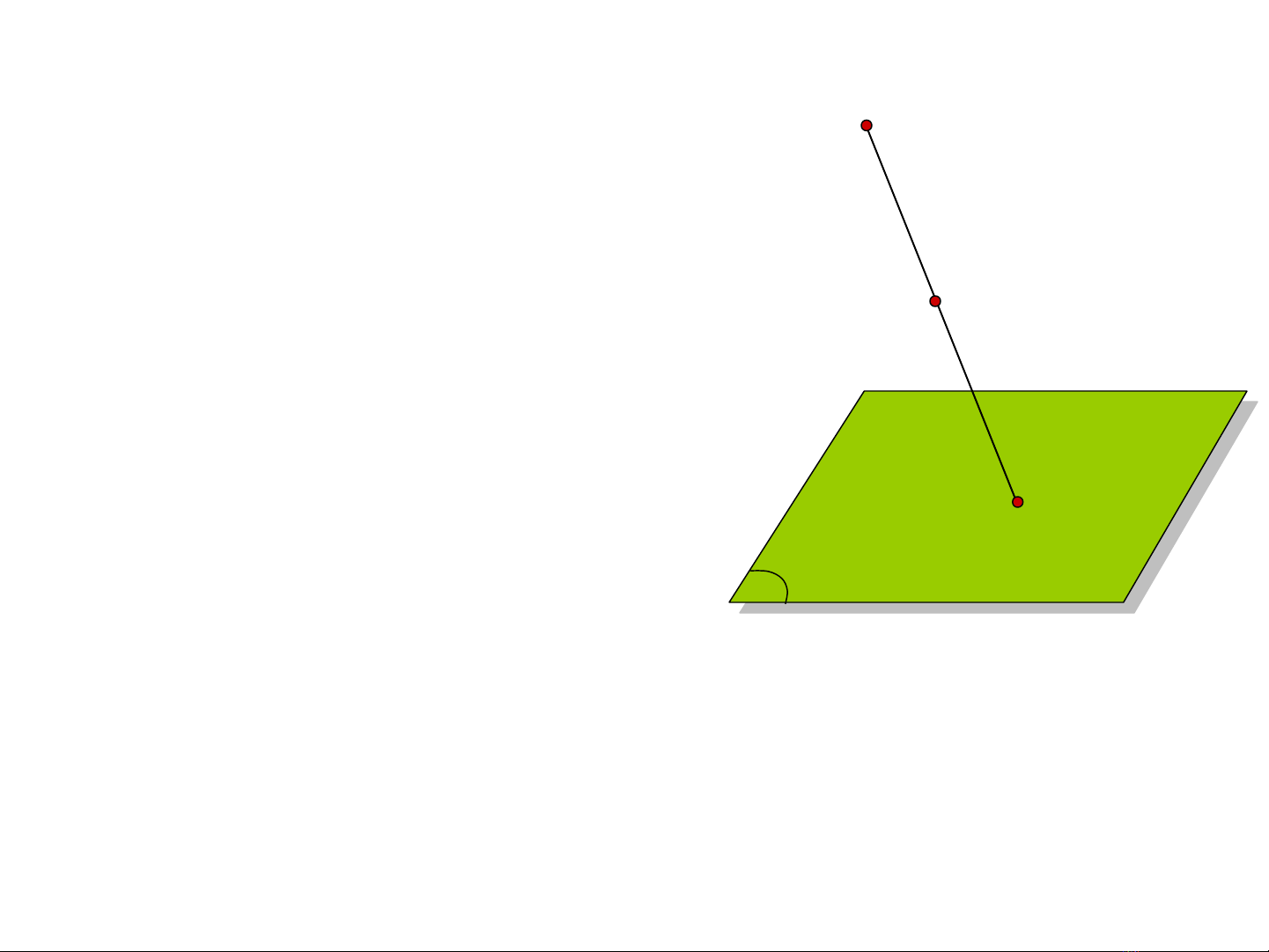
a) Xây dựng phép chiếu
- Cho mặt phẳng Π, một điểm S không thuộc
Π và một điểm A bất kỳ.
- Gọi A’ là giao của đường thẳng SA với mặt
phẳng Π.
*Ta có các định nghĩa sau:
+ Mặt phẳng Π gọi là mặt phẳng hình chiếu
+ Điểm S gọi là tâm chiếu
+ Điểm A’ gọi là hình chiếu xuyên tâm của
điểm A lên mặt phẳng hình chiếu Π
+ Đường thẳng SA gọi là tia chiếu của điểm A
A
A’
Hình 1.1 Xây dựng phép
chiếu xuyên tâm
S
П
5
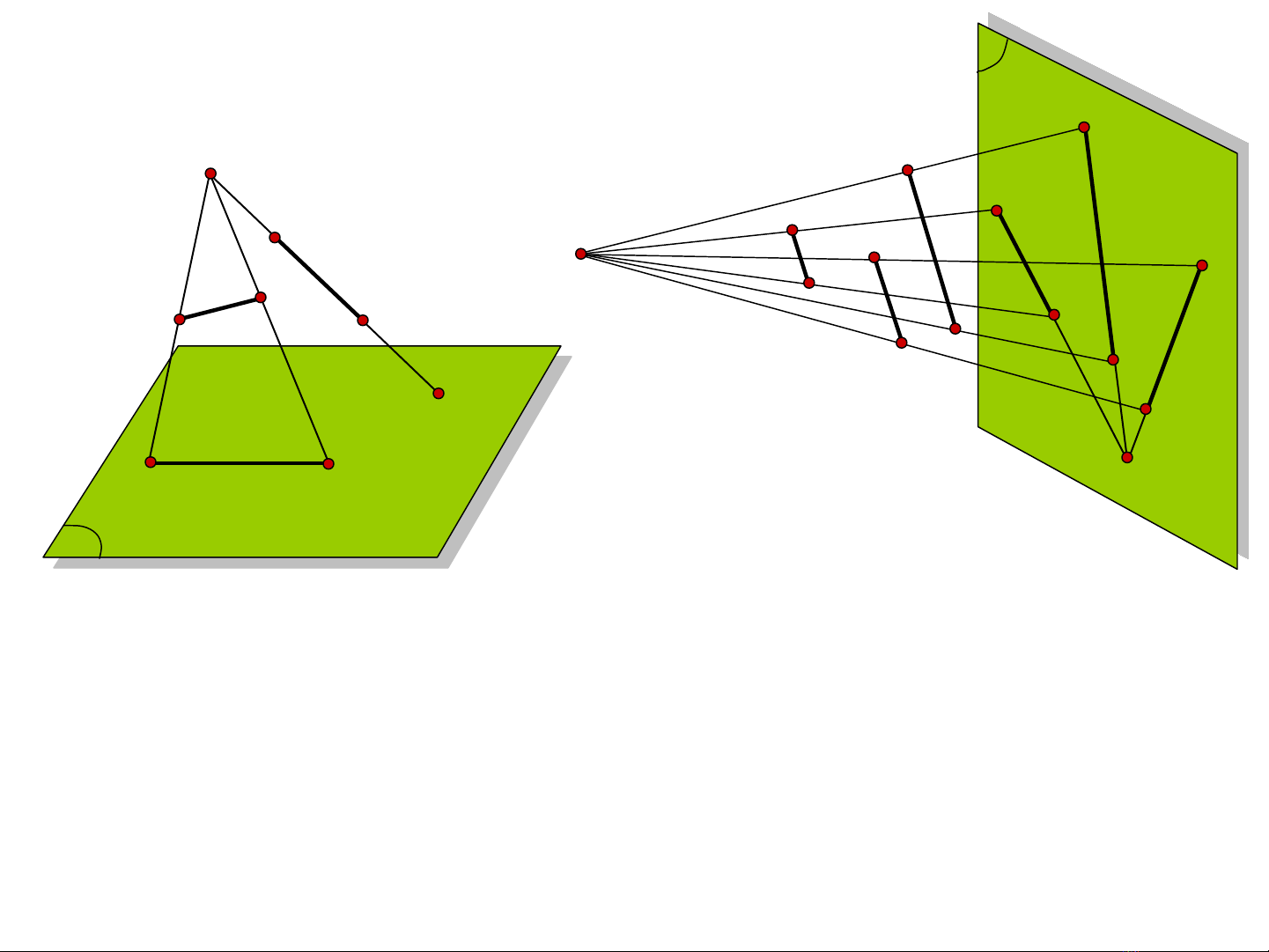
- Nếu AB là đoan thẳng không đi qua tâm chiếu S thì hình chiếu xuyên tâm của nó
là một đoan thẳng A’B’.
- Nếu CD là đường thẳng đi qua tâm chiếu S thì C’=D’.(Hình chiếu suy biến) (Hình
0.2.a)
- Hình chiếu xuyên tâm của các đường thẳng song song nói chung là các đường
đồng quy. (Hình 0.2.b)
A
A’
Hình 1.2a,b Tính chất phép chiếu xuyên tâm
S
B’
B
C
D
C’=D’
b) Tính chất phép chiếu
S
C’
A’
B’
D’
F’
E’
T’
a)
b)
A
B
E
FD
C
П
П