Khóa học LTĐH môn Toán Moon.vn – Thầy ĐẶNG VIỆT HÙNG Facebook: LyHung95
Tham gia trọn vẹn khóa LTĐH môn Toán tại Moon.vn để đạt điểm số cao nhất trong kỳ TSĐH!
1) Véc tơ pháp tuyến, phương trình tổng quát của mặt phẳng
(
)
2 2 2
; ; , 0
= + + >
n A B C A B C có ph
ươ
ng vuông góc v
ớ
i (
P
)
đượ
c g
ọ
i là
véc tơ pháp tuyến
c
ủ
a (
P
).
(
P
)
đ
i qua
đ
i
ể
m
(
)
; ;
M x y z
và có véc t
ơ
pháp tuy
ế
n
(
)
; ;
=
n A B C
thì có ph
ươ
ng trình
đượ
c vi
ế
t d
ạ
ng
(
)
(
)
(
)
(
)
0 0 0
: 0.
P A x x B y y C z z
− + − + − =
(P) có véc t
ơ
pháp tuy
ế
n
(
)
; ;
=
n A B C
thì có ph
ươ
ng trình t
ổ
ng quát
(
)
: 0.
P Ax By Cz D
+ + + =
(P)
đ
i qua ba
đ
i
ể
m phân bi
ệ
t A, B, C thì có véc t
ơ
pháp tuy
ế
n
;
P
n AB AC
=
(P)
đ
i qua
đ
i
ể
m A và
song song
v
ớ
i (Q) thì ta ch
ọ
n cho
=
P Q
n n
(
P
)
đ
i qua
đ
i
ể
m
A
và
vuông góc
v
ớ
i hai m
ặ
t ph
ẳ
ng phân bi
ệ
t (
α
), (
β
) thì
;
α
α β
β
⊥
→ =
⊥
P
P
P
n n
n n n
n n
(P)
đ
i qua
đ
i
ể
m A và song song v
ớ
i hai véc t
ơ
;
a b
thì
;
⊥
→ =
⊥
P
P
P
n a
n a b
n b
(P)
đ
i qua
đ
i
ể
m A, B và vuông góc v
ớ
i (
α
) thì ;
α
α
⊥
→ =
⊥
P
P
P
n AB
n AB n
n n
Ví dụ 1:
[ĐVH].
Viết phương trình mặt phẳng (P) trong các trường hợp sau:
a) qua M(1; 1; 2) và có véc tơ pháp tuyến
(
)
= −
1; 2;1 .
n
b) qua M(2; 0; 1) và song song v
ớ
i (Q): x + 2y + 5z
−
−−
−
1 = 0.
c) qua M(3;
−
−−
−
1; 0) và vuông góc v
ớ
i hai m
ặ
t ph
ẳ
ng (Q): 4x + z
−
−−
−
1 = 0; (R): 2x + 3y
−
−−
−
z
−
−−
−
5 = 0.
H
ướ
ng d
ẫ
n gi
ả
i:
a) (P)
đ
i qua M(1; 1; 2) và có véc t
ơ
pháp tuy
ế
n
(
)
1; 2;1
= −
nnên có ph
ươ
ng trình
(
)
(
)
(
)
(
)
: 1. 1 2. 1 1. 2 0 2 1 0
− − − + − = ⇔ − + − =
P x y z x y z
b) (P) // (Q) nên
// ,
P Q
n n
ch
ọ
n
(
)
(
)
(
)
(
)
(
)
1;2;5 :1. 2 2. 0 5. 1 0
= = → − + − + − =
P Q
n n P x y z
(
)
: 2 5 7 0.
→ + + − =
P x y z
c) (P) qua vuông góc v
ớ
i hai m
ặ
t ph
ẳ
ng (Q): 4x + z
−
1 = 0; (R): 2x + 3y
−
z
−
5 = 0 nên có véc t
ơ
pháp tuy
ế
n
( ) ( ) ( )
4 0 1
; 3;6;12 3 1; 2; 4 1; 2; 4
2 3 1
⊥
→ = = = − = − − −
⇒
= − −
−
⊥
P Q
P Q R P
P R
n n n n n n
n n
Khi
đ
ó (P) có ph
ươ
ng trình
(
)
(
)
1. 3 2. 1 4 0 2 4 5 0
− − + − = ⇔ − − − =
x y z x y z
Ví d
ụ
2:
[
Đ
VH].
Cho A(–1; 2; 3), B(2; –4; 3), C(4; 5; 6).
a)
Vi
ế
t ph
ươ
ng trình m
ặ
t ph
ẳ
ng
đ
i qua A và nh
ậ
n vect
ơ
(
)
1; 1;5
−
n làm vect
ơ
pháp tuy
ế
n
b)
Vi
ế
t ph
ươ
ng trình m
ặ
t ph
ẳ
ng
đ
i qua A bi
ế
t r
ằ
ng hai véct
ơ
có giá song song ho
ặ
t n
ằ
m trong m
ặ
t ph
ẳ
ng
đ
ó là
(
)
(
)
1;2; 1 , 2; 1;3
− −
a b
c) Vi
ế
t ph
ươ
ng trình m
ặ
t ph
ẳ
ng qua C và vuông góc v
ớ
i
đườ
ng th
ẳ
ng AB.
d)
Vi
ế
t ph
ươ
ng trình m
ặ
t ph
ẳ
ng trung tr
ự
c c
ủ
a
đ
o
ạ
n AC.
e)
Vi
ế
t ph
ươ
ng trình (ABC).
Ví d
ụ
3:
[
Đ
VH].
Cho A(–1; 2; 1), B(1; –4; 3), C(–4; –1; –2).
a)
Vi
ế
t ph
ươ
ng trình m
ặ
t ph
ẳ
ng
đ
i qua I(2; 1; 1) và song song v
ớ
i (ABC).
b)
Vi
ế
t ph
ươ
ng trình m
ặ
t ph
ẳ
ng qua A và song song v
ớ
i (P): 2x – y – 3z – 2 = 0.
03. PHƯƠNG TRÌNH MẶT PHẲNG
Thầy Đặng Việt Hùng
Trang 1
Khóa học LTĐH môn Toán Moon.vn – Thầy ĐẶNG VIỆT HÙNG Facebook: LyHung95
Tham gia trọn vẹn khóa LTĐH môn Toán tại Moon.vn để đạt điểm số cao nhất trong kỳ TSĐH!
c) Viết phương trình mặt phẳng qua hai điểm A, B và vuông góc với (Q): 2x – y + 2z – 2 = 0.
d) Viết phương trình mặt phẳng qua A, song song với Oy và vuông góc với (R): 3x – y – 3z – 1 = 0.
e) Viết phương trình mặt phẳng qua C song song với (Oyz).
Ví dụ 4: [ĐVH].
Viết phương trình mặt phẳng (α) đi qua hai điểm A, B và vuông góc với mặt phẳng (β) cho trước,
với:
a)
( )
3 1 1 2 1 4
2 3 1 0
− −
− + − =
β
( ; ; ), ( ; ; )
:
A B
x y z
b)
( )
2 1 3 4 2 1
2 3 2 5 0
− − −
+ − + =
β
( ; ; ), ( ; ; )
:
A B
x y z
c)
( )
2 1 3 4 7 9
3 4 8 5 0
− − −
+ − − =
β
( ; ; ), ( ; ; )
:
A B
x y z
d)
( )
3 1 2 3 1 2
2 2 2 5 0
− − −
− − + =
β
( ; ; ), ( ; ; )
:
A B
x y z
Ví dụ 5:
[ĐVH].
Vi
ế
t ph
ươ
ng trình m
ặ
t ph
ẳ
ng (α)
đ
i qua
đ
i
ể
m
M
và giao tuy
ế
n c
ủ
a hai m
ặ
t ph
ẳ
ng (
P
), (
Q
) cho tr
ướ
c,
v
ớ
i:
a)
(
)
(
)
(
)
1 2 3 2 3 5 0 3 2 5 1 0
− − + − = − + − =
; ; , : ,M P x y z Q : x y z
b)
(
)
(
)
(
)
2 1 1 4 0 3 1 0
− − + − = − + − =
; ; , : ,M P x y z Q : x y z
c)
(
)
(
)
(
)
3 4 1 19 6 4 27 0 42 8 3 11 0
− − + = − + + =
; ; , : ,M P x y z Q : x y z
d)
(
)
(
)
(
)
0 0 1 5 3 2 5 0 2 1 0
− + − = − − − =
; ; , : , :M P x y z Q x y z
Ví dụ 6:
[ĐVH].
Vi
ế
t ph
ươ
ng trình m
ặ
t ph
ẳ
ng (α) qua giao tuy
ế
n c
ủ
a hai m
ặ
t ph
ẳ
ng (
P
), (
Q
),
đồ
ng th
ờ
i song song
v
ớ
i m
ặ
t ph
ẳ
ng (
R
) cho tr
ướ
c, v
ớ
i:
a)
2 4 0 3 0 2 0
P y z Q x y z R x y z
( ): , ( ): , ( ):
+ − = + − − = + + − =
b)
4 2 5 0 4 5 0 2 19 0
P x y z Q y z R x y
( ): , ( ): , ( ):
− + − = + − = − + =
c)
3 2 0 4 5 0 2 7 0
P x y z Q x y R x z
( ): , ( ): , ( ):
− + − = + − = − + =
Ví dụ 7:
[ĐVH].
Vi
ế
t ph
ươ
ng trình m
ặ
t ph
ẳ
ng (α) qua giao tuy
ế
n c
ủ
a hai m
ặ
t ph
ẳ
ng (
P
), (
Q
),
đồ
ng th
ờ
i vuông góc
v
ớ
i m
ặ
t ph
ẳ
ng (
R
) cho tr
ướ
c, v
ớ
i:
a)
2 3 4 0 2 3 5 0 2 3 2 0
P x y Q y z R x y z
( ): , ( ): , ( ):
+ − = − − = + − − =
b)
2 4 0 3 0 2 0
P y z Q x y z R x y z
( ): , ( ): , ( ) :
+ − = + − + = + + − =
c)
2 4 0 2 5 0 2 3 6 0
P x y z Q x y z R x y z
( ): , ( ): , ( ):
+ − − = + + + = − − + =
d)
3 2 0 4 5 0 2 7 0
P x y z Q x y R x z
( ): , ( ): , ( ):
− + − = + − = − + =
2) Một số dạng phương trình mặt phẳng đặc biệt
Mặt phẳng (xOy):
véc t
ơ
pháp tuy
ế
n là
Oz
và
đ
i qua
g
ố
c t
ạ
o
độ
nên có ph
ươ
ng trình là
z
= 0.
Đặ
c bi
ệ
t, m
ặ
t ph
ẳ
ng song song v
ớ
i (
Oxy
) có ph
ươ
ng trình
là
z
−
a
= 0.
Mặt phẳng (yOz):
véc t
ơ
pháp tuy
ế
n là
Ox
và
đ
i qua
g
ố
c t
ạ
o
độ
nên có ph
ươ
ng trình là
x
= 0.
Đặ
c bi
ệ
t, m
ặ
t ph
ẳ
ng song song v
ớ
i (
Oyz
) có ph
ươ
ng trình
là
x
−
a
= 0.
Mặt phẳng (xOz):
véc t
ơ
pháp tuy
ế
n là
Oy
và
đ
i qua
g
ố
c t
ạ
o
độ
nên có ph
ươ
ng trình là
y
= 0.
Đặ
c bi
ệ
t, m
ặ
t ph
ẳ
ng song song v
ớ
i (
Oxz
) có ph
ươ
ng trình
là
y
−
a
= 0.
Mặt phẳng trung trực:
Cho hai
đ
i
ể
m
A, B
. Khi
đ
ó m
ặ
t ph
ẳ
ng trung tr
ự
c c
ủ
a
AB
đ
i qua trung
đ
i
ể
m
I
c
ủ
a
AB
và nh
ậ
n
AB
làm véc t
ơ
pháp
Trang 2
Khóa học LTĐH môn Toán Moon.vn – Thầy ĐẶNG VIỆT HÙNG Facebook: LyHung95
Tham gia trọn vẹn khóa LTĐH môn Toán tại Moon.vn để đạt điểm số cao nhất trong kỳ TSĐH!
tuyến.
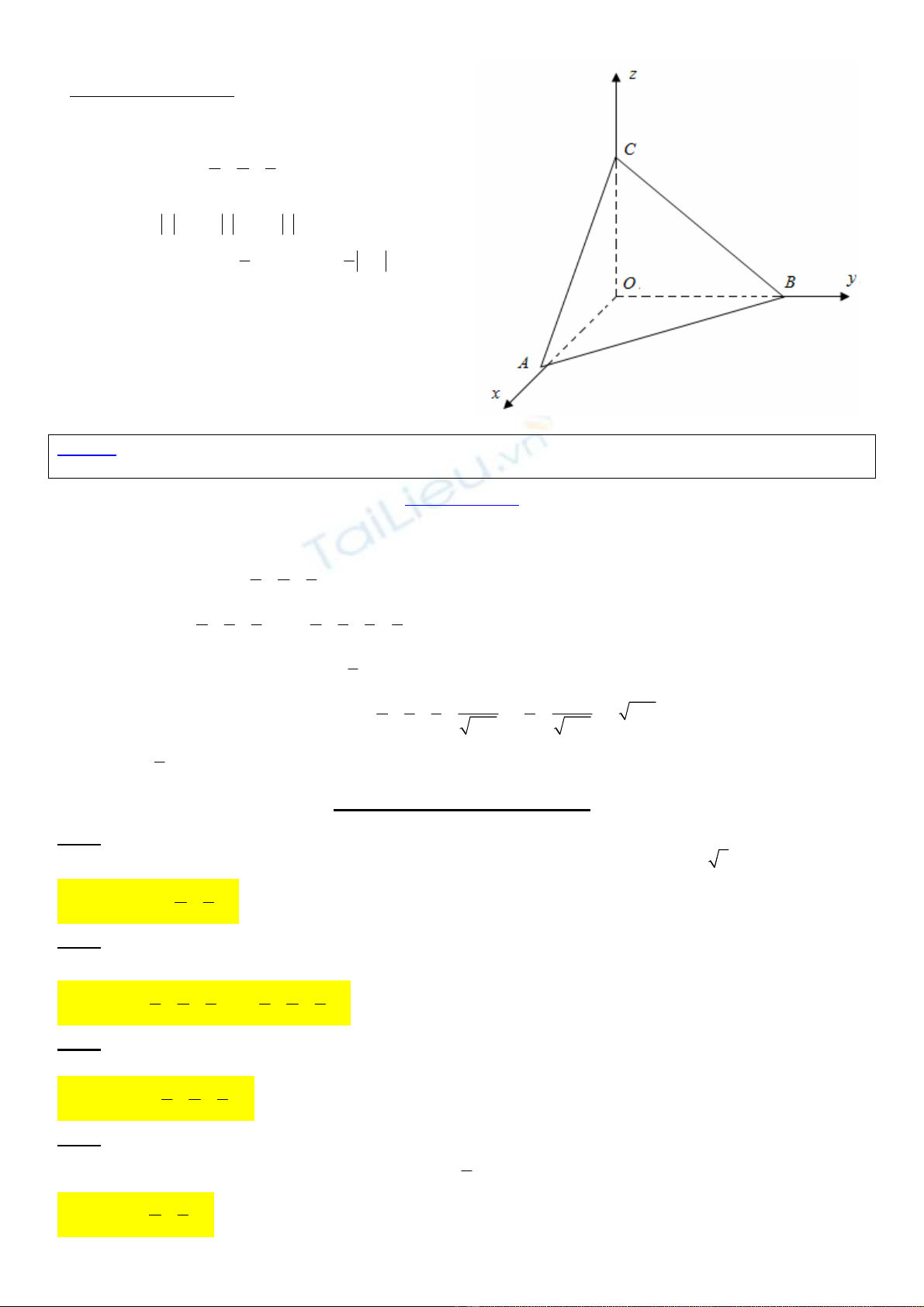
Phương trình mặt chắn:
Nếu mặt phẳng (P) cắt ba trục tọa độ lần lượt tại các
điểm
(
)
(
)
(
)
;0;0 , 0; ;0 , 0;0;
A a B b C c
thì (
P) có ph
ươ
ng
trình
đ
o
ạ
n ch
ắ
n:
( )
: 1
+ + =
x y z
P
a b c
.
Một số đặc điểm của mặt chắn:
+ Độ dài ; ;
= = =
OA a OB b OC c
+ Thế tích tứ diện 1 1
. .
6 6
= =
OABC
V OAOB OC abc
+ Chân đường cao hạ từ O xuống (ABC) trùng với trực
tâm H của tam giác ABC.
Ví dụ 1: [ĐVH].
Viết phương trình mặt phẳng đi qua M(2; 2; 2) cắt các tia Ox, Oy,Oz tại các điểm A, B, C sao
cho thể tích tứ diện OABC nhỏ nhất.
Hướng dẫn giải:
• Giả sử mặt phẳng cần lập cắt các tia Ox, Oy, Oz tại A(a; 0; 0), B(0; b; 0), C(0; 0; c). Do mặt phẳng cắt các tia nên
Ta có a, b, c > 0
Phương trình mặt chắn
( )
: 1.
+ + =
x y z
P
a b c
• Do
( )
2 2 2 1 1 1 1
1
2
∈ → + + = ⇔ + + =
M P
a b c a b c
Ta có
1
; ;
6
= = = → =
OABC
OA a OB b OC c V abc
• Do a, b, c là ba số dương nên theo Côsi ta có
3
3 3
1 1 1 3 1 3
6 216
2
+ + ≥ ⇔ ≥ ⇔ ≥ ⇔ ≥abc abc
a b c abc abc
min
1
.216 36 36 6
6
→ ≥ =
⇒
= ⇔ = = =
OABC
V V a b c , t
ừ
đ
ó ta
đượ
c ph
ươ
ng trình (P): x + y + z – 6 = 0
BÀI TẬP LUYỆN TẬP:
Bài 1:
[ĐVH].
Cho
đ
i
ể
m A(1; 0; 0) và m
ặ
t ph
ẳ
ng (P): y – z + 1 = 0. Vi
ế
t ph
ươ
ng trình m
ặ
t ph
ẳ
ng
đ
i qua A, vuông góc
v
ớ
i (P) và c
ắ
t các tr
ụ
c Oy, Oz l
ầ
n l
ượ
c t
ạ
i các
đ
i
ể
m B, C sao cho di
ệ
n tích tam giác ABC b
ằ
ng
6.
Đ
/s:
( )
: 1
2 2
y z
ABC x
± ± =
Bài 2:
[ĐVH].
Cho
đ
i
ể
m A(2; 0; 0) và
đ
i
ể
m M(2; 3; 2). Vi
ế
t ph
ươ
ng trình m
ặ
t ph
ẳ
ng (
α
)
đ
i qua A, M sao cho (
α
) c
ắ
t
các tr
ụ
c Oy, Oz l
ầ
n l
ượ
c t
ạ
i các
đ
i
ể
m B, C sao cho
2
OABC
V
=
, v
ớ
i O là g
ố
c t
ọ
a
độ
.
Đ
/s:
( )
: 1; 1
2 3 2 2 3 2
x y z x y z
ABC
+ − = − + =
Bài 3:
[ĐVH].
Cho
đ
i
ể
m A(–2; 0; 0) và m
ặ
t ph
ẳ
ng (P): x + 2z + 3 = 0. Vi
ế
t ph
ươ
ng trình m
ặ
t ph
ẳ
ng
đ
i qua A, vuông
góc v
ớ
i (P) và c
ắ
t các tr
ụ
c Oy, Oz l
ầ
n l
ượ
c t
ạ
i các
đ
i
ể
m B, C sao cho
4
OABC
V
=
Đ
/s:
( )
: 1
2 3 4
x y z
ABC
− + + =
Bài 4:
[ĐVH].
Cho
đ
i
ể
m B(0; 3; 0) và
đ
i
ể
m M(1; -3; 2). Vi
ế
t ph
ươ
ng trình m
ặ
t ph
ẳ
ng (
α
)
đ
i qua B, M sao cho (
α
) c
ắ
t
các tr
ụ
c Ox, Oz l
ầ
n l
ượ
c t
ạ
i các
đ
i
ể
m A, C sao cho
7
2
ABC
S
=
, v
ớ
i O là g
ố
c t
ọ
a
độ
.
Đ
/s:
( )
α
: 1
3 2
y z
x
+ + =
Trang 3
Khóa học LTĐH môn Toán Moon.vn – Thầy ĐẶNG VIỆT HÙNG Facebook: LyHung95
Tham gia trọn vẹn khóa LTĐH môn Toán tại Moon.vn để đạt điểm số cao nhất trong kỳ TSĐH!
Bài 5: [ĐVH]. Viết pt mp đi qua M(2; 1; 4) và cắt các trục Ox, Oy, Oz tại các điểm A, B, C sao cho OA = OB = OC.
Bài 6: [ĐVH]. Viết phương trình mặt phẳng đi qua M(2; 2; 2) cắt các tia Ox, Oy,Oz tại các điểm A, B, C sao cho thể
tích tứ diện OABC nhỏ nhất.
Bài 7: [ĐVH]. Viết phương trình mặt phẳng đi qua M(1; 1; 1) cắt các tia Ox, Oy,Oz lần lược tại các điểm A, B, C sao
cho tam giác ABC cân tại A, đồng thời M là trọng tâm tam giác ABC.
Trang 4