PHAÀN 1: COÂNG TAÙC ÑAÁT
CHÖÔNG 2: TÍNH KHOÁI LÖÔÏNG COÂNG TAÙC ÑAÁT
MUÏC LUÏC
Chöông 2: Tính khoái löôïng coâng taùc ñaát
2.1. Tính khoái löôïng hoá moùng
2.3. Tính khoái löôïng san baèng maët ñaát
2.2. Tính khoái löôïng coâng trình ñaát chaïy daøi
2.4. Xaùc ñònh höôùng vaø khoaûng caùch vaän chuyeån khi san neàn
2.1.Tính khoái löôïng hoá moùng
2.1.Tính khoái löôïng hoá moùng
Kích thöôùc hoá moùng :
c
a
b
d
H
❑Hoá ñaøo coù kích thöôùc maët baèng vaø chieàu saâu lôùn: kích thöôùc ñaùy hoá moùng lôùn hôn
ñaùy moùng khoaûng 2.0m
❑Neáu laø raõnh moùng thì chieàu roäng
raõnh ñaøo lôùn hôn chieàu roäng moùng
nhaø 0.3 –0.5m
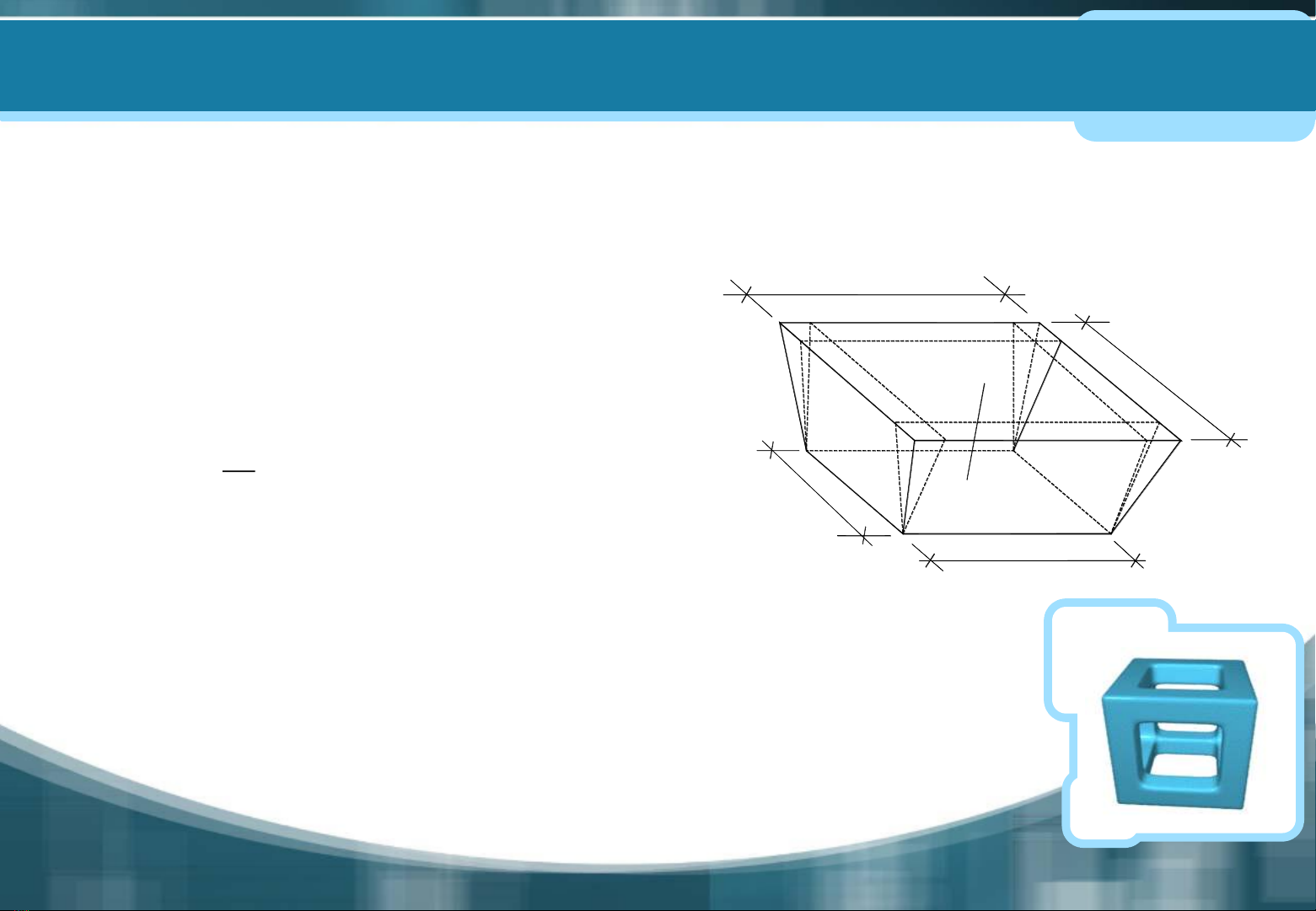
Theå tích hoá moùng :
( )( )
6
H
V ab c a d b dc= + + + +


Trong ñoù:
a,b: chieàu daøi vaø chieàu roäng maët ñaùy;
c,d: chieàu daøi vaø chieàu roäng maët treân;
H: chieàu saâu hoá moùng
2.2.Tính khoái löôïng coâng trình ñaát chaïy daøi