BÀI GIẢNG CƠ HỌC KẾT CẤU
CHƯƠNG 7
7.1 KHÁI NIỆM
Chương 7: Phương pháp chuyển vị 2
1. Ý tưởng phương pháp chuyển vị
Nếu biết chuyển vị đầu thanh đường đàn hồi y
M=-EIy” Q = -EIy”’ N.
7.1 KHÁI NIỆM
Chương 7: Phương pháp chuyển vị 3
Có 2 dạng liên kết giữa các thanh
Nút cứng (liên kết hàn): Chuyển vị (thẳng, xoay) của
nút chính là chuyển vị các đầu thanh qui tụ vào nút.
Nút khớp (liên kết khớp): Chỉ xét chuyển vị thẳng vì
các đầu thanh qui tụ vào nút có thể xoay tự do quanh
khớp. Góc xoay các đầu thanh không ảnh hưởng đến
nội lực trong thanh.
Nút cứng Nút khớp
Vì các đầu thanh qui tụ vào nút nên có thể lấy chuyển nút
(thẳng & xoay) làm ẩn số.
7.1 KHÁI NIỆM
Chương 7: Phương pháp chuyển vị 4
2. Các giả thiết
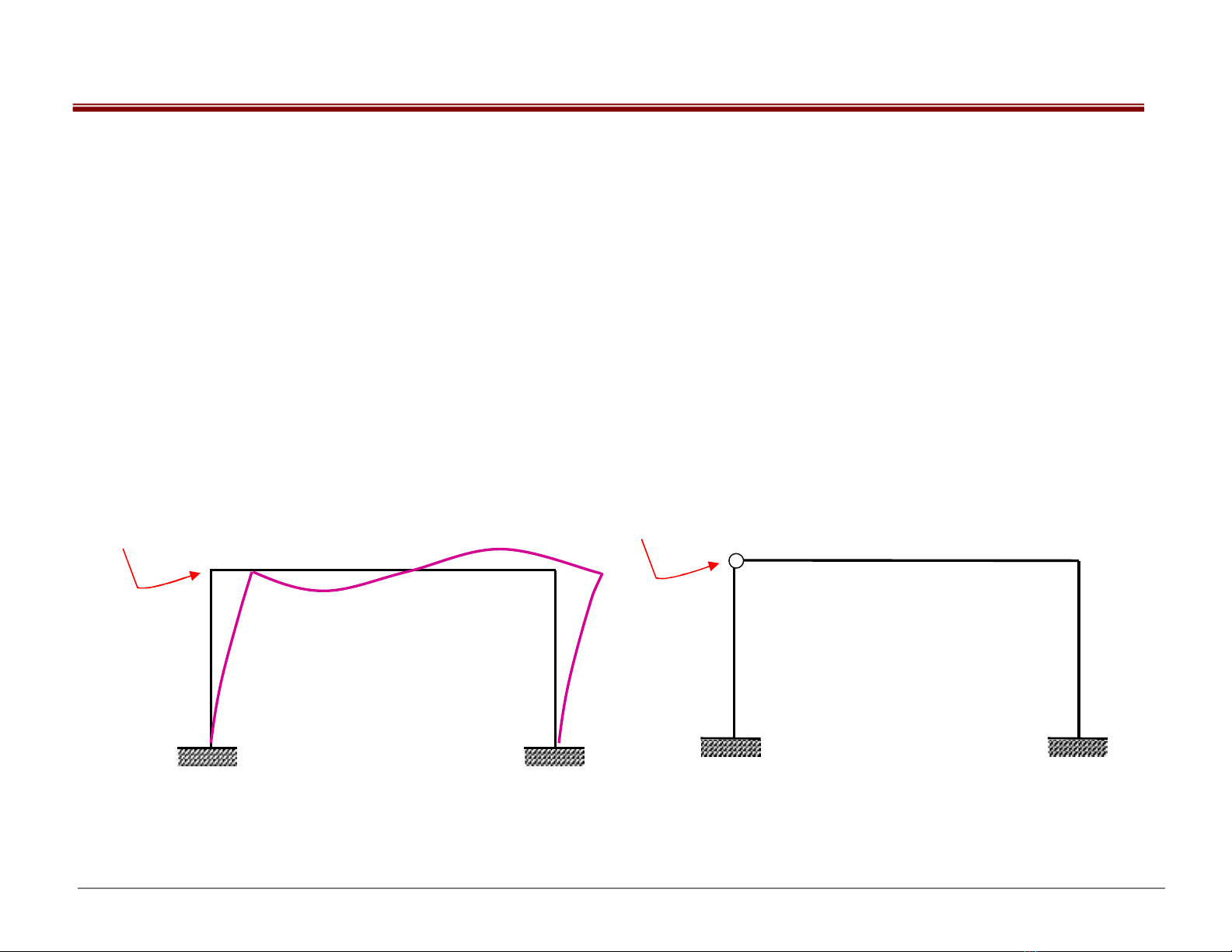
1) Nút tuyệt đối cứng: góc xoay của các đầu thanh qui tụ
vào nút cứng là như nhau và là góc xoay của nút.
A B
L
A’
B’
L
3) Bỏ qua ảnh hưởng của lực dọc, lực cắt khi tính chuyển vị.
4) Vật liệu đàn hồi tuyến tính
5) Chuyển vị và biến dạng bé.
6) Áp dụng được nguyên lý cộng tác dụng.
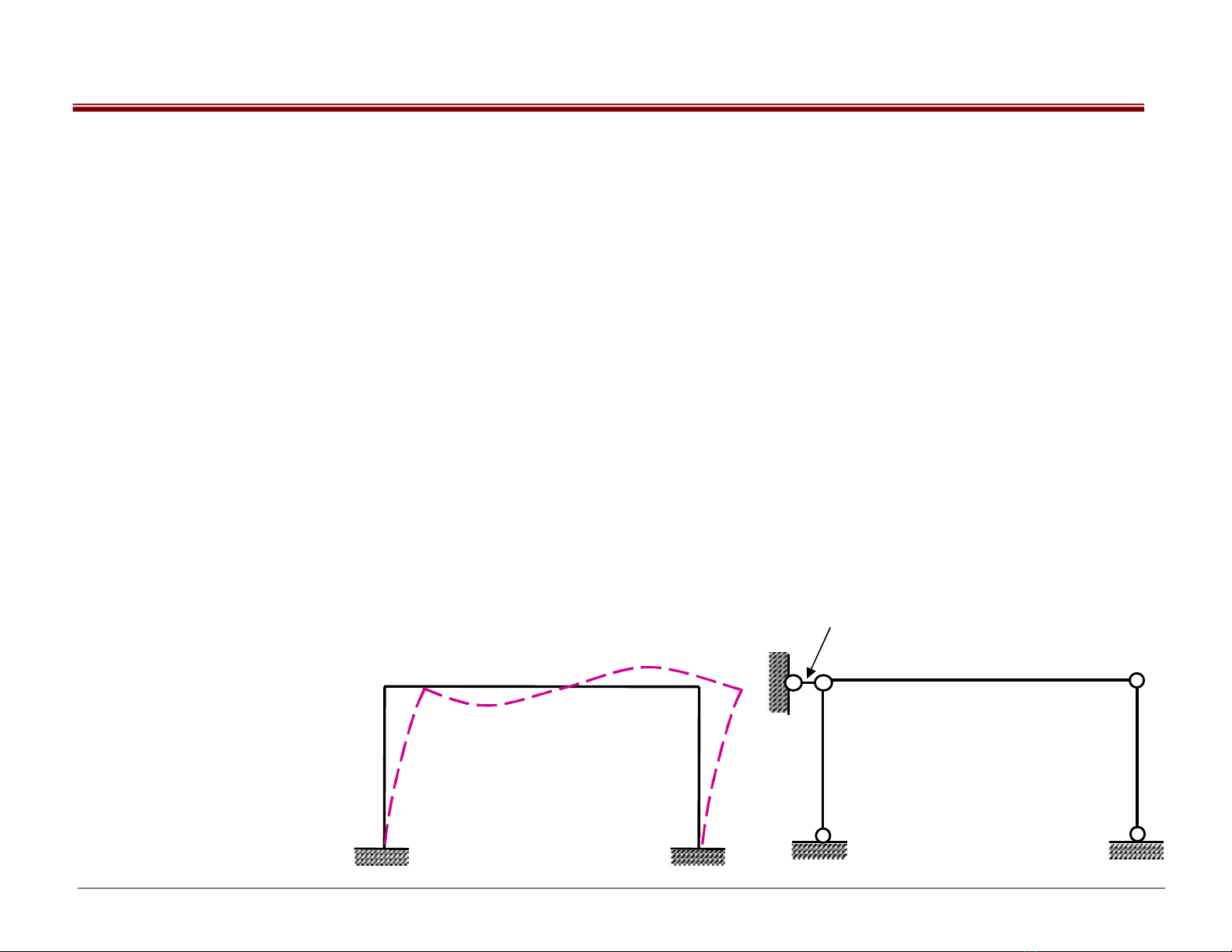
2) Chiều dài theo phương ban
đầu không đổi (bỏ qua N ,
trừ khi tính đến nhiệt độ)
7.2 NÔI DUNG PHƯƠNG PHÁP CHUYỂN VỊ
Chương 7: Phương pháp chuyển vị 5
1. Xác định ẩn số: Ẩn số của pp chuyển vị là chuyển
vị xoay và thẳng của tất cả các nút trong kết cấu.
Số ẩn số n theo pp chuyển vị là: n = n1 + n2
n1= số góc xoay của các nút cứng = số nút cứng.
n2= số chuyển vị thẳng độc lập của các nút
= số bậc tự do hệ khớp
= số liên kết thanh (liên kết phụ) đặt thêm để hệ
thay khớp bất biến hình, đủ liên kết. Liên kết phụ