Options, Futures, and Other Derivatives, 6th Edition, Copyright © John C. Hull 2005 13.1
Mô hình Black-Scholes-
Merton
Ch ng 13ươ
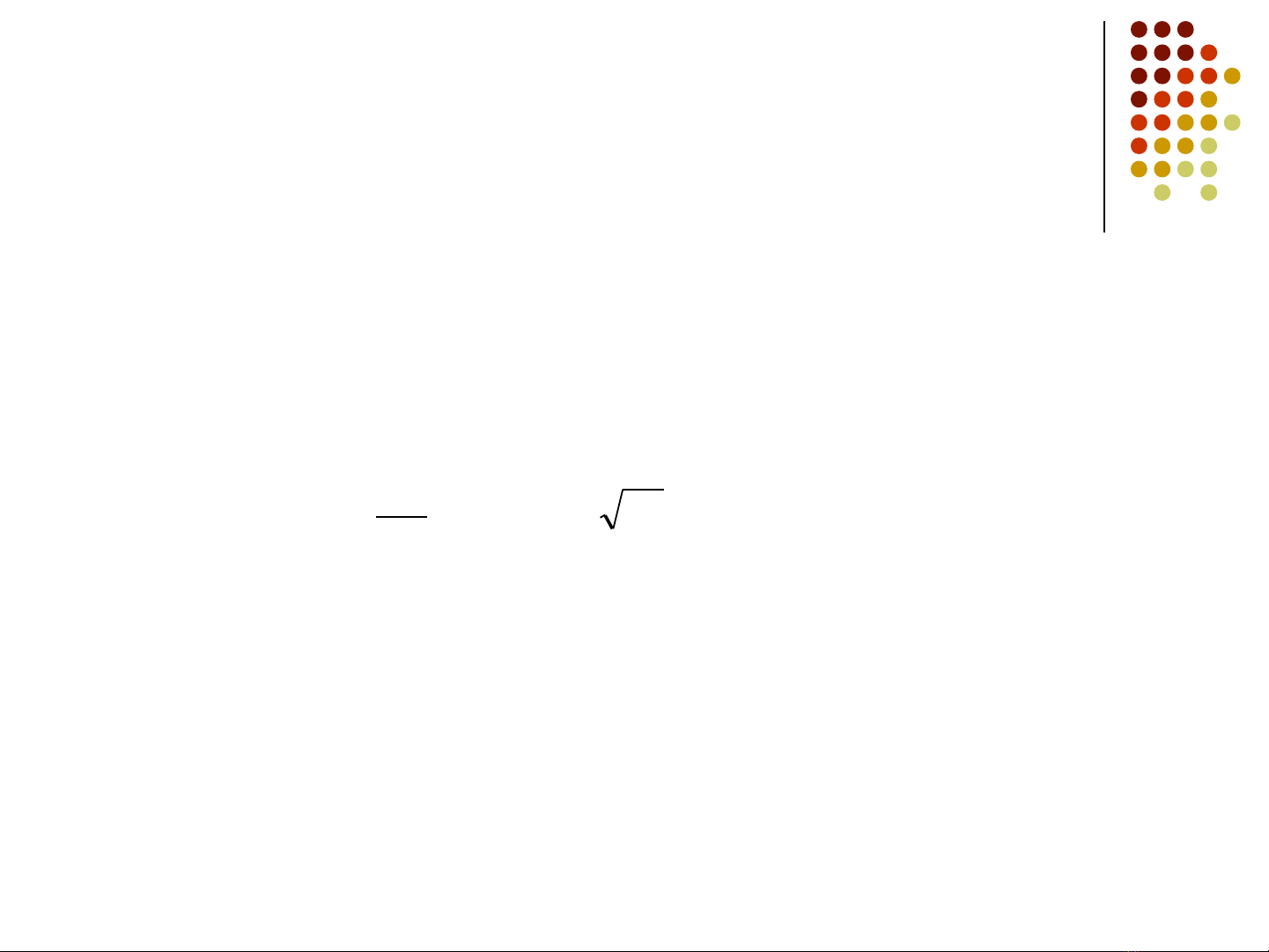
Options, Futures, and Other Derivatives, 6th Edition,
Copyright © John C. Hull 2005
13.2
Gi đ nh giá c phi uả ị ổ ế
Xem xét m t c phi u có giá là ộ ổ ế S
Trong m t th i gian ng n ộ ờ ắ ∆t, l i nhu n c a ợ ậ ủ
c phi u đ c phân ph i chu n: ổ ế ượ ố ẩ
v i ớµ là l i nhu n kỳ v ng và ợ ậ ọ σ là đ bi n ộ ế
đ ng (đ r i ro - volatility)ộ ộ ủ
( )
tt
S
S∆∆≈
∆
σµφ
,
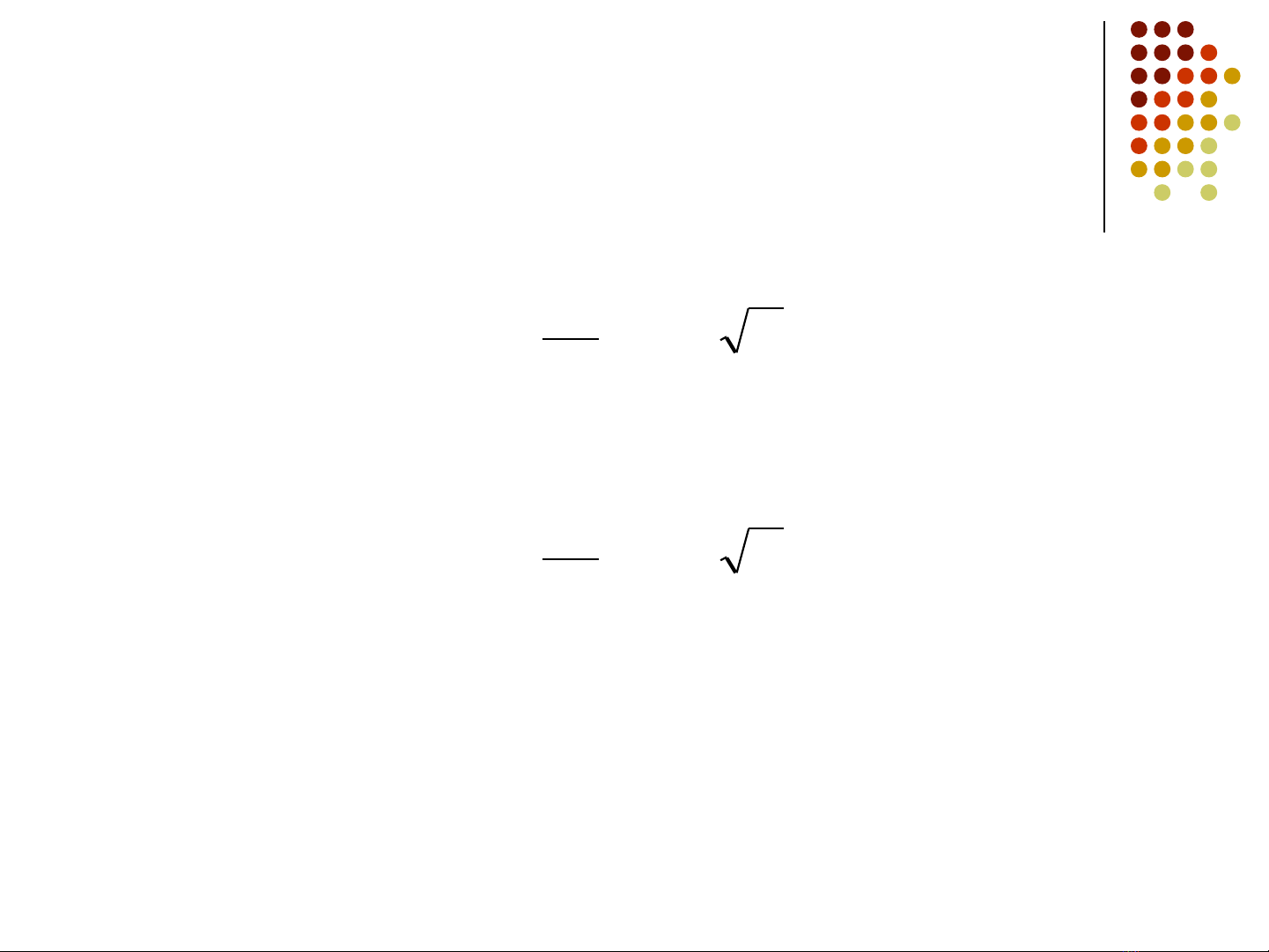
Options, Futures, and Other Derivatives, 6th Edition,
Copyright © John C. Hull 2005
13.3
Thu c tính c a Logarit chu n ộ ủ ẩ
(Các ph ng trình 13.2 và 13.3, trang 282)ươ
T gi đ nh trên, ta có:ừ ả ị
Vì logarit c a ủST là logarit chu n (log c s ẩ ơ ố
10 - ND) nên ST có phân ph i logarit ố
chu n. ẩ
ln ln ,
ln ln ,
S S T T
S S T T
T
T
− ≈ −
≈ + −
0
2
0
2
2
2
φ µ σσ
φ µ σσ
or
Options, Futures, and Other Derivatives, 6th Edition,
Copyright © John C. Hull 2005
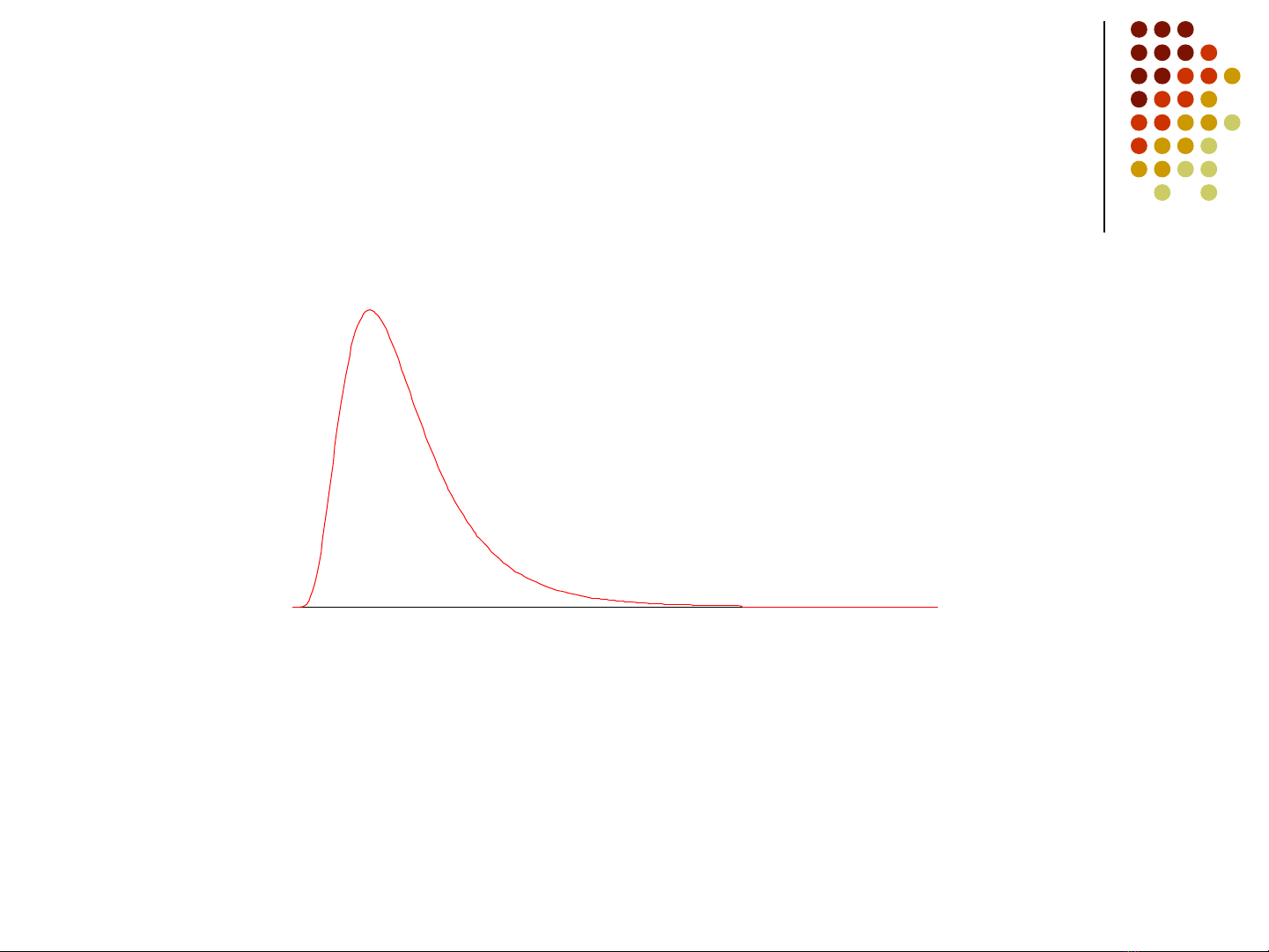
Phân ph i Log chu nố ẩ
E S S e
S S e e
T
T
T
T T
( )
( ) ( )
=
= −
0
0
22
2
1
var
µ
µ σ

Options, Futures, and Other Derivatives, 6th Edition,
Copyright © John C. Hull 2005
13.5
Su t sinh l i g p lãi liên t c, ấ ợ ộ ụ x
(Các ph ng trình 13.6 và 13.7, trang 283)ươ
,
2
ln
1
=
2
0
0
−≈
=
T
x
S
S
T
x
eSS
T
xT
T
σσ
µφ
ho cặ
ho cặ


























