Cho hàm ba biến w=f(x;y;z)xác định trong miền đóng, bị
chặn Ω⊆R3.
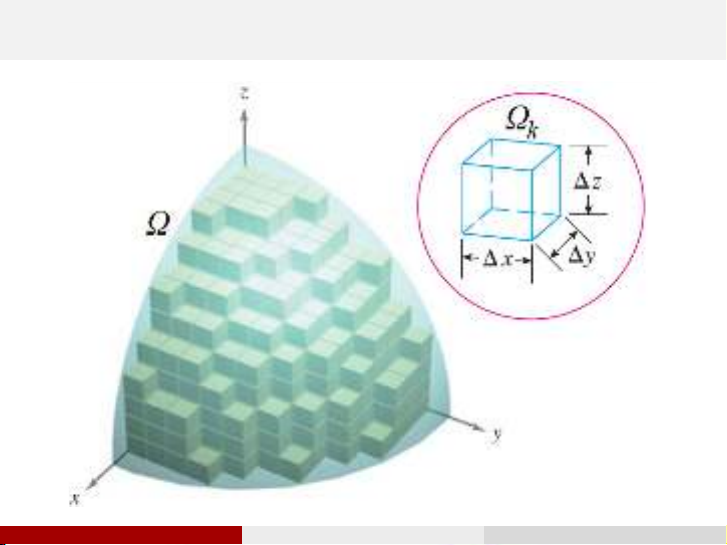
Chia miền Ωthành nmiền nhỏ Ω1,Ω2,. . .,Ωnkhông
giẫm nhau, có diện tích tương ứng là
∆v1,∆v2,...,∆vn.
Trong mỗi miền Ωk, lấy một điểm bất kỳ Mk(xk;yk;zk).
Lập tổng tích phân: Sn=
n
X
k=1
f(xk, yk;zk).∆vk.
Snphụ thuộc vào cách chia Ωvà cách lấy Mk.
BM Toán-Cơ-Tin học (Khoa KHCB) Chương 2. TÍCH PHÂN BỘI BA 28/9/2020 4 / 25
Đặt d(Ωk)là đường kính của Ωk.
Nếu giới hạn
S= lim
n→+∞
( max
1≤k≤nd(Ωk)→0)
Sn= lim
n→+∞
( max
1≤k≤nd(Ωk)→0) "n
X
k=1
f(xk;yk;zk).∆vk#
tồn tại hữu hạn, không phụ thuộc vào cách chia miền Ω,
không phụ thuộc vào cách lấy Mkthì ta nói fkhả tích
trên Ω, và tích phân bội ba của ftrên Ωcó giá trị S, ký
hiệu ZZZ
Ω
f(x;y;z)dv=S.
trong đó dvlà yếu tố thể tích. Ta cũng có thể viết
dv=dxdydz.
BM Toán-Cơ-Tin học (Khoa KHCB) Chương 2. TÍCH PHÂN BỘI BA 28/9/2020 5 / 25
