1
Chương 5. GIỚI HẠN VÀ LIÊN TỤC CỦA HÀM MỘT BIẾN
NỘI DUNG CHƯƠNG 5: GIỚI HẠN VÀ LIÊN
TỤC CỦA HÀM MỘT BIẾN
5.1. Giới hạn
5.2. Hàm số liên tục
Toán Cao Cấp - ThS. Lê Trường Giang
2
Chương 5. GIỚI HẠN VÀ LIÊN TỤC CỦA HÀM MỘT BIẾN
Giải tích toán học lấy giới hạn làm phương pháp
để nghiên cứu hàm số. Người ta phân biệt giới hạn của
dãy với giới hạn của hàm. Các khái niệm này chỉ được
hoàn chỉnh vào thế kỉ 19, dù rằng các nhà bác học cổ Hi
Lạp cũng đã nghĩ tới chúng. Chỉ cần biết rằng
Archimède (thế kỉ 3 trước công nguyên) đã tính được
diện tích của chỏm hình parabol, bằng một quá trình mà
ngày nay chúng ta gọi là chuyển đến giới hạn. Một lớp
các hàm quan trọng nghiên cứu trong giải tích toán học
là các hàm số liên tục.
Toán Cao Cấp - ThS. Lê Trường Giang
3
Chương 5. GIỚI HẠN VÀ LIÊN TỤC CỦA HÀM MỘT BIẾN
5.1. GIỚI HẠN
5.1.1. Giới hạn của dãy số
1) Cấp số cộng và cấp số nhân
a) Cấp số cộng
+ Định nghĩa: dãy được gọi là một cấp số cộng với
công sai d nếu thỏa:
+ Định lý:
Toán Cao Cấp - ThS. Lê Trường Giang
4
n
x
n n 1
x x d

n1
n 1 2 n 1 n
x x n 1 d
n
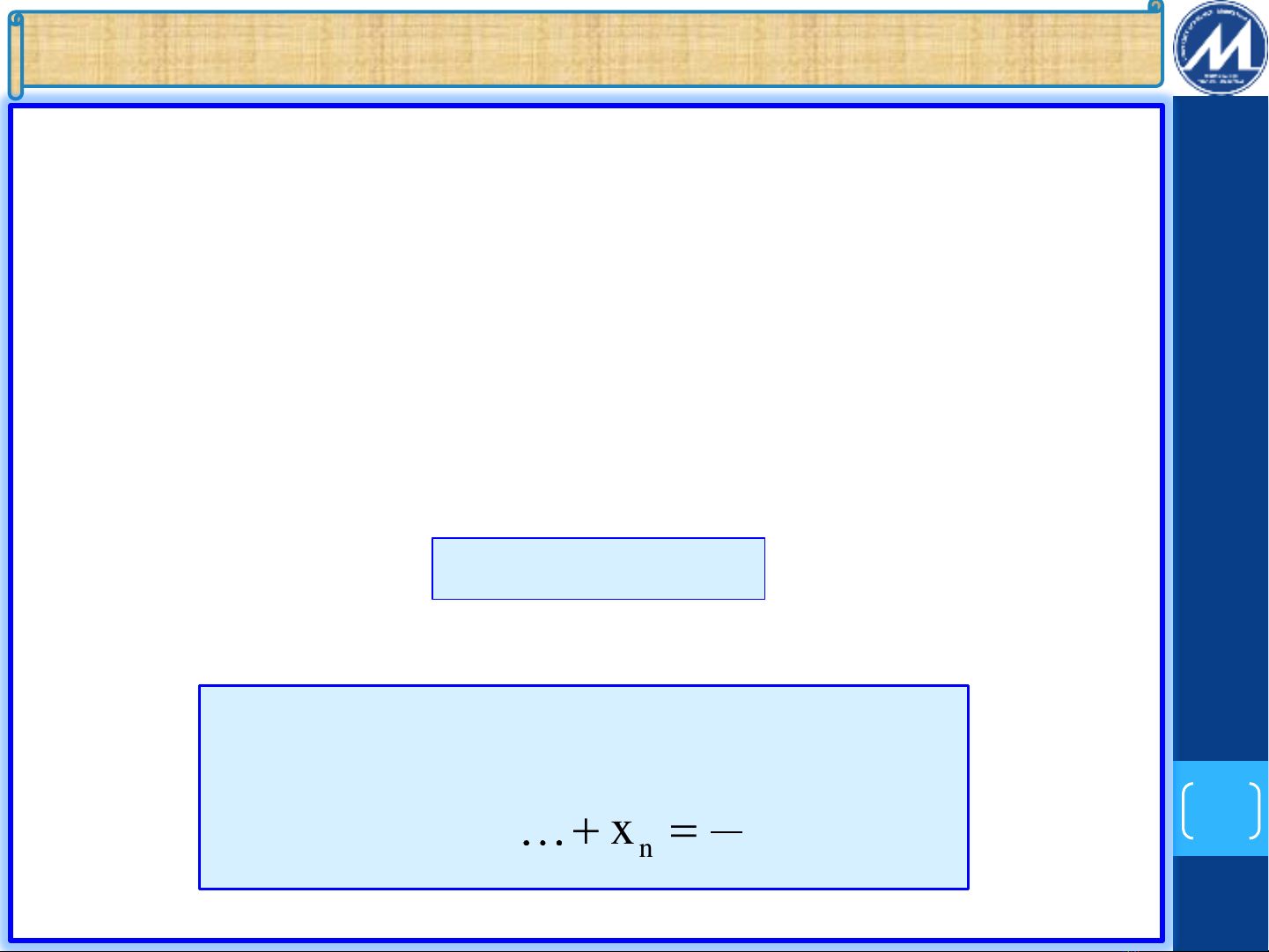
S x x x x x
2
Chương 5. GIỚI HẠN VÀ LIÊN TỤC CỦA HÀM MỘT BIẾN
b) Cấp số nhân
+ Định nghĩa: dãy được gọi là một cấp số nhân với
công bội q nếu thỏa:
+ Định lý:
Toán Cao Cấp - ThS. Lê Trường Giang
5
n
x
n n 1
x qx
n1
n1
n
n 1 2 n 1
x x q
1q
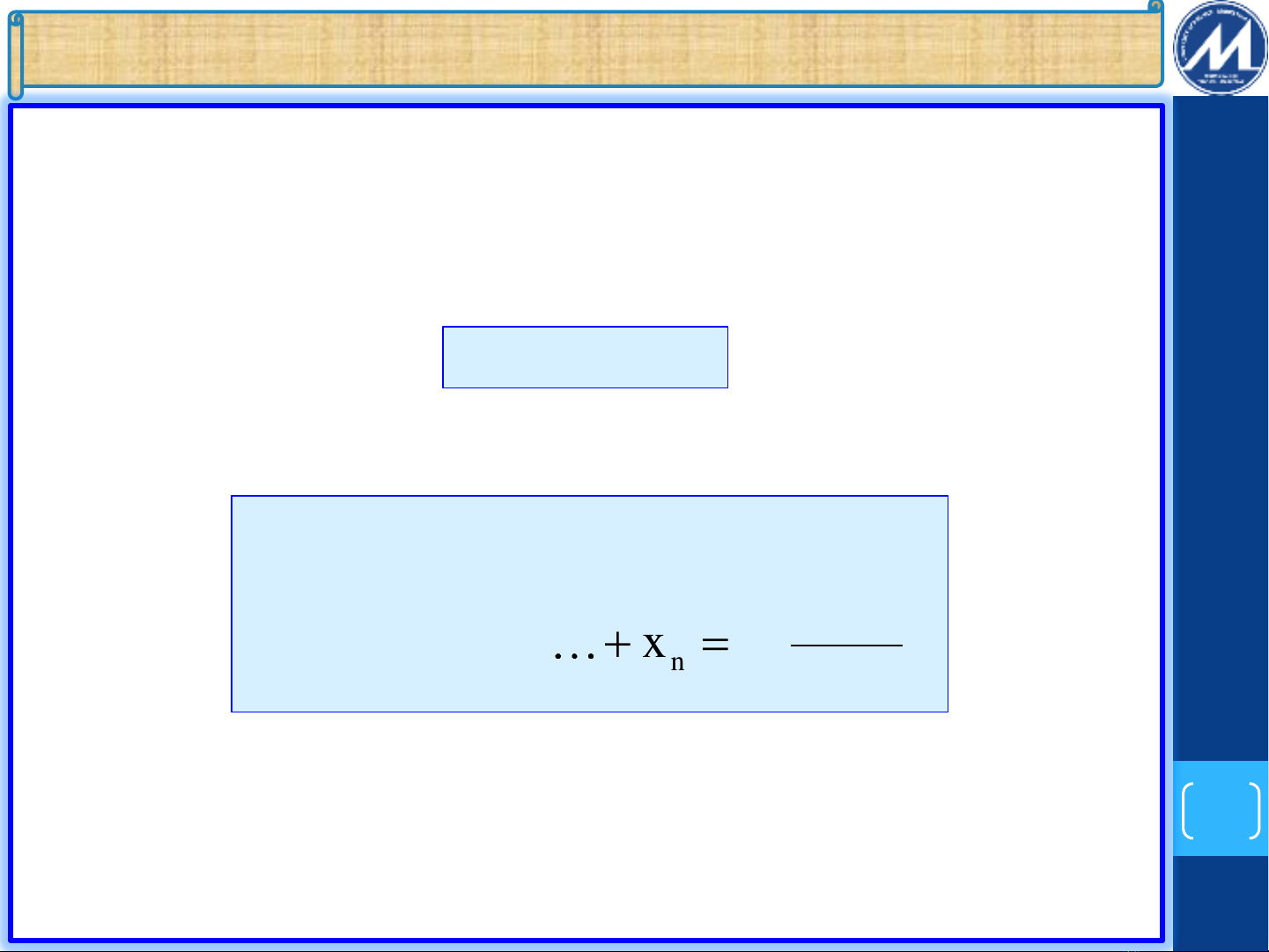
S x x x x 1q