
Chương
Chương 2 T
2 Tí
ích phân Fourier & bi
ch phân Fourier & bi
n ñ
n ñ
i Fourier
i Fourier
Bài ging Toán KThut 2012
2.1 Tích phân Fourier
2.2 Phép bin ñi Fourier
2.3 ng dng ca tích phân Fourier và bin ñi Fourier
2.4 Các hàm bt thưng và bin ñi Fourier ca chúng
1

Hàm tun hoàn
2
2.1 T
2.1 Tí
ích phân Fourier
ch phân Fourier
Hàm chxác ñnh
trên khong kín
Chui Fourier
Hàm không tun hoàn
Chui Fourier
Tích phân Fourier
Bài ging Toán KThut 2012
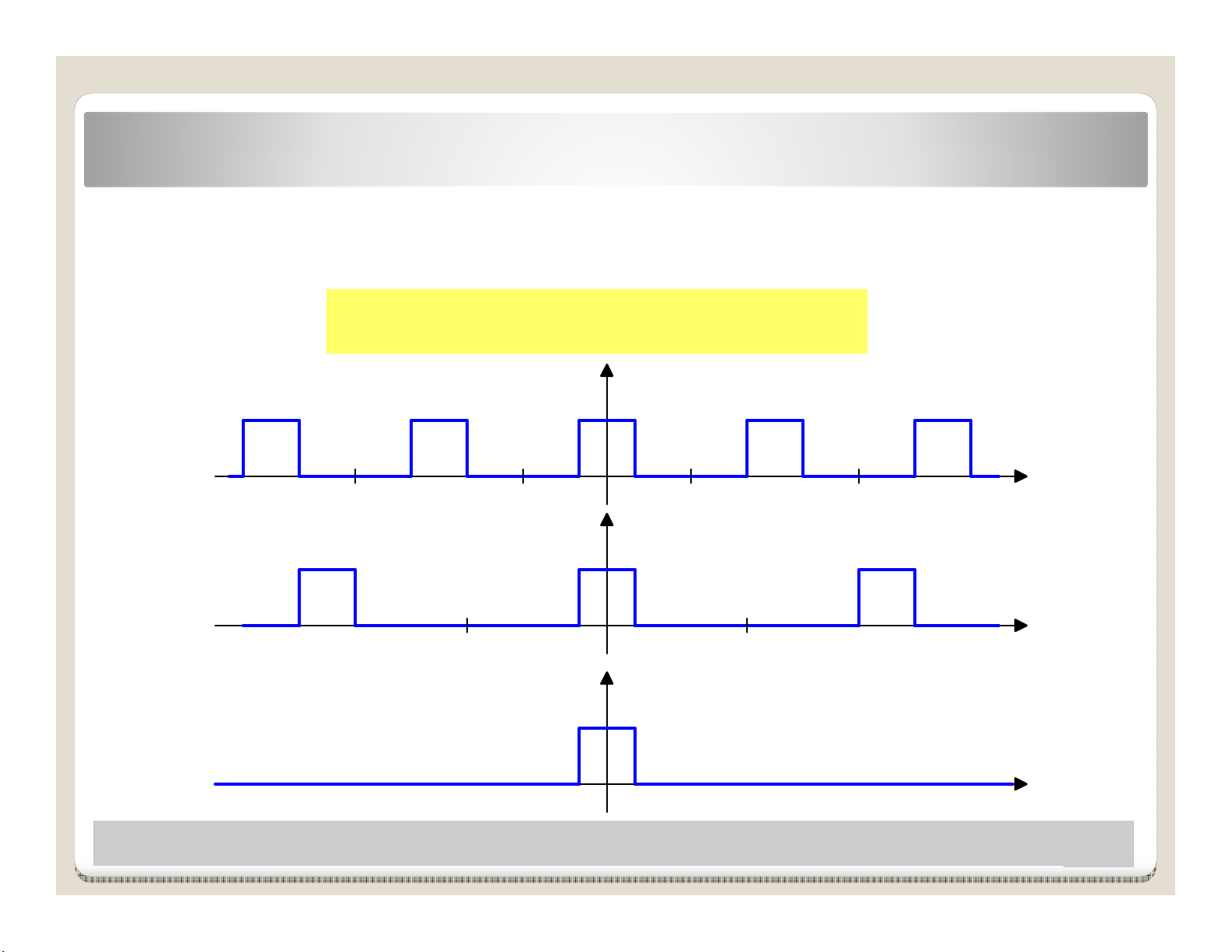
Bài ging Toán KThut 2012 3
Khác bit gia hàm tun hoàn và không tun hoàn ?
Chu kỳT hu hn và vô hn
2.1.1 T
2.1.1 Tí
ích phân Fourier
ch phân Fourier
→ ∞
→ ∞
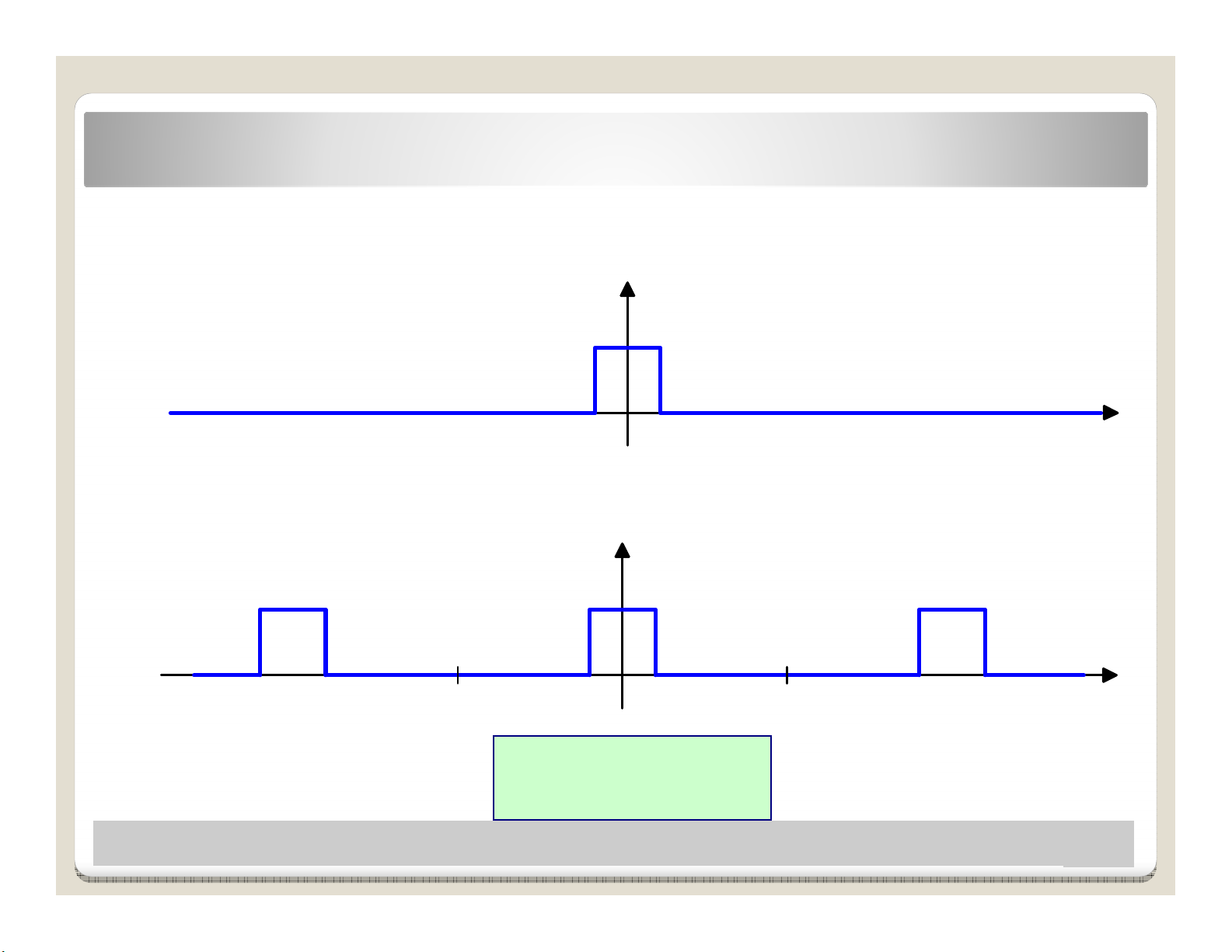
Cn tìm khai trin Fourier cho f(t) trong khong (-∞,+∞)
4
2.1.1 T
2.1.1 Tí
ích phân Fourier
ch phân Fourier
Ta sbt ñu tfΤ(t)
→ ∞
Dthy rng →∞
=
Bài ging Toán KThut 2012
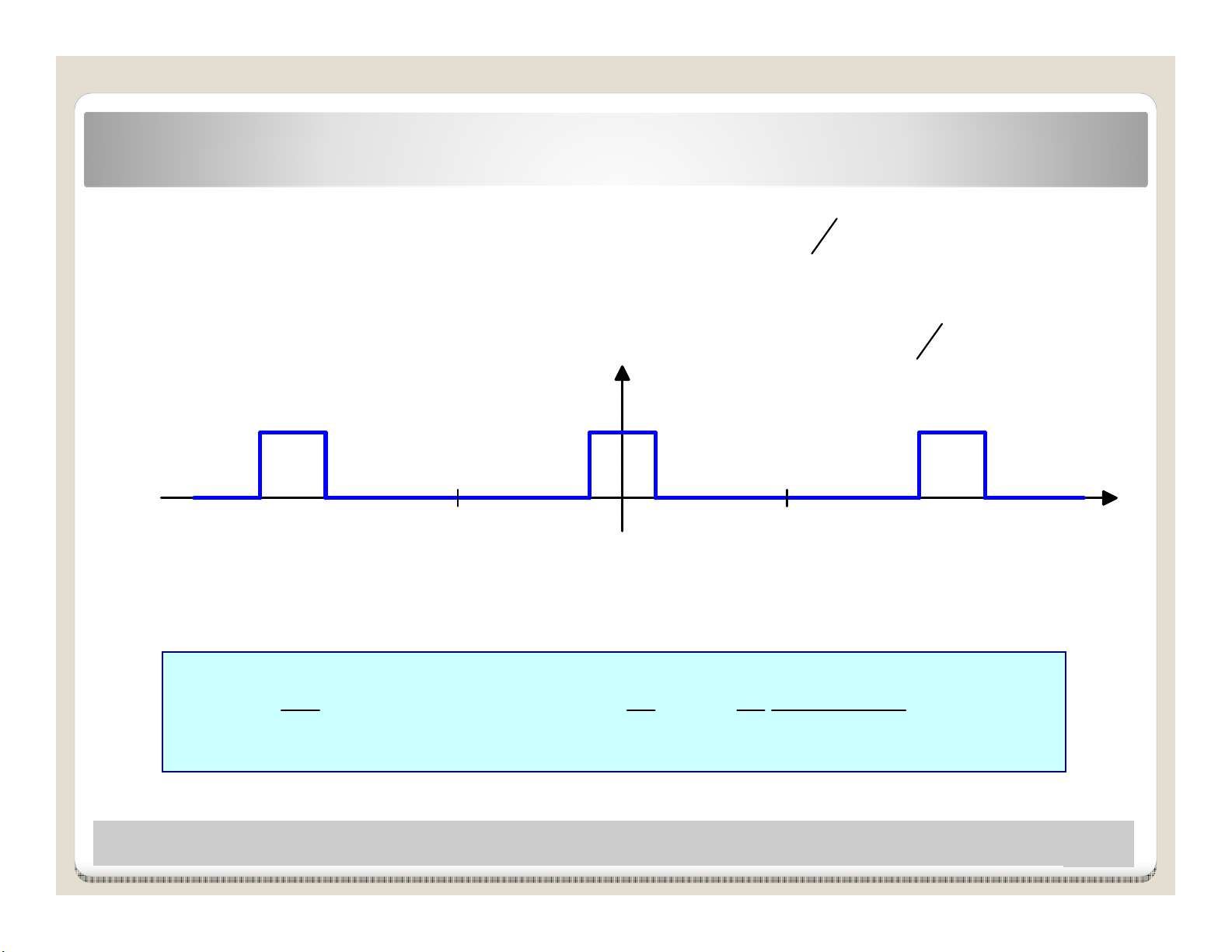
Hàm tun hoàn fT(t)
có ñnh nghĩa trong
1 chu kỳlà
5
2.1.1 T
2.1.1 Tí
ích phân Fourier
ch phân Fourier
− < < −
= − < <
< <
fT(t) có khai trin Fourier là :
ω
ω ω
ω
+∞ +∞
= =
= + = +
∑ ∑
Bài ging Toán KThut 2012


























