Baìi táûp Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
BAÌI TÁÛP CHÆÅNG 1 :
CHUYÃØN ÂÄÜNG CUÍA VÁÛT RÀÕN
BAÌI TÁÛP AÏP DUÛNG :
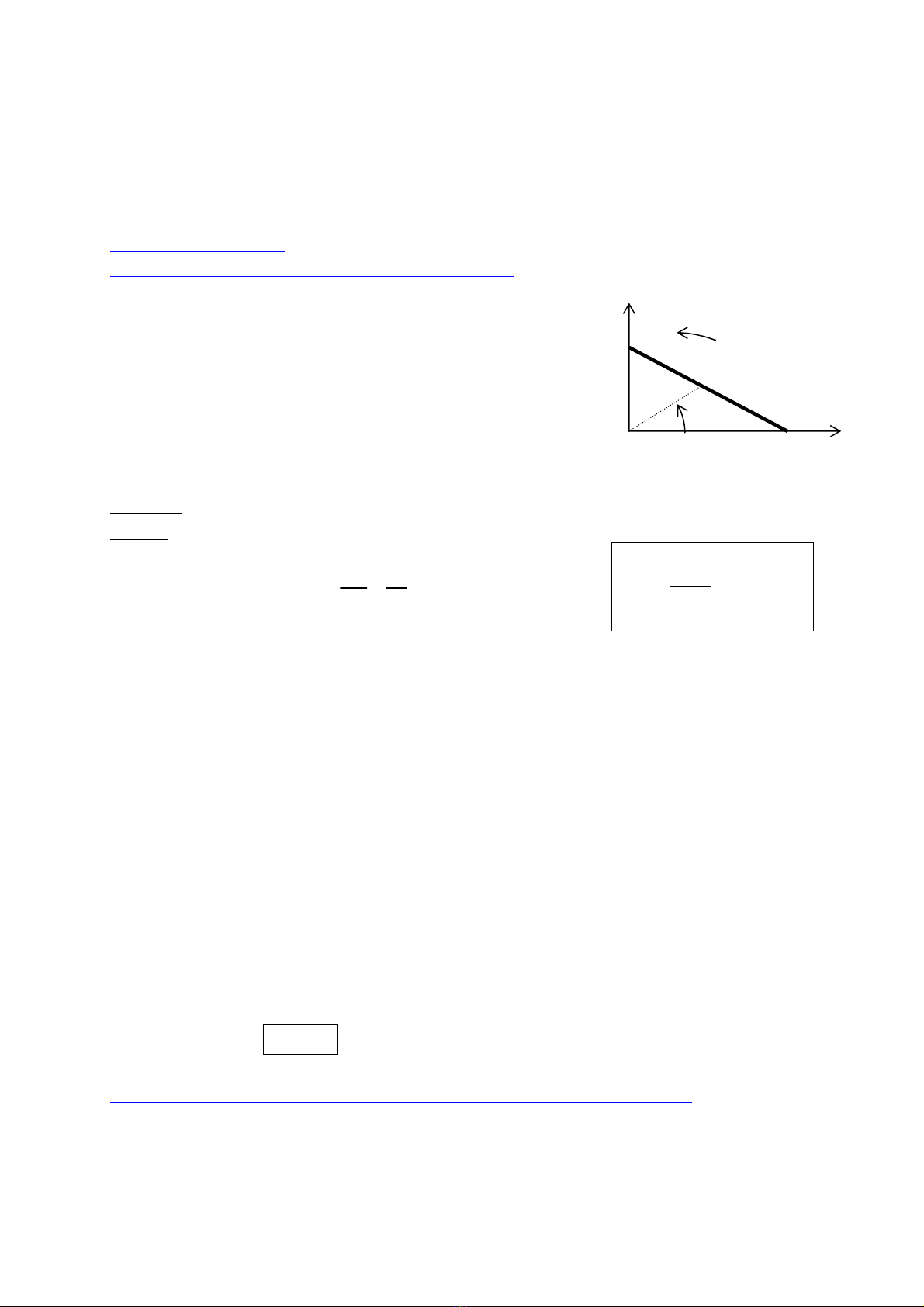
@ AÏp duûng 1 (Trang 29) : Chuyãøn âäüng cuía thanh
Mäüt thanh AB âäöng cháút chiãöu daìi 2b, khäúi tám G nàòm taûi âiãøm
giæîa cuía thanh. Thanh tæûa trãn màût âáút nàòm ngang vaì gäúi trãn
bæïc tæåìng thàóng âæïng. Vë trê cuía thanh âæåüc xaïc âënh båíi goïc
, thay âäøi khi thanh træåüt taûi A vaì B. (, )Ox OG
α
=JJK JJJK
x
A
G
B
O
y
z
α
:
⊕
1) Xaïc âënh træûc tiãúp caïc thaình pháön cuía váûn täúc v( )G
K
cuía âiãøm
G theo α vaì theo âaûo haìm cuía α.
2) Suy ra veïctå quay
Ω
K
cuía thanh.
Baìi giaíi :
Cáu 1 :
Tam giaïc OAB vuäng : 2
22
AB b
OG ⇒
b===
cos
sin
0
b
OG b
α
α
⎧
⎪
=⎨
⎪
⎩
JJJG ⇒
sin
v( ) cos
0
b
dOG
Gb
dt
α
α
α
α
−
⎧
⎪
==
⎨
⎪
⎩
JJJG
G
(1)
Cáu 2 :
(Caïch tçm : Viãút biãøu thæïc cuía váûn täúc v( )G
G
theo hai caïch khaïc nhau - âaûo haìm træûc tiãúp vaì
bàòng quan hãû váûn täúc hai âiãøm thuäüc cuìng váût ràõn cáön tim vectå quay - vaì so saïnh)
Thanh AB chuyãøn âäüng song phàóng våïi vectå quay z
e
=Ω
G
G
.
Hai âiãøm A vaì G cuìng thuäüc thanh AB : v( ) v( )GA A=+Ω×G
J
JJG
G
G
G
Trong âoï : laì vectå quay cuía thanh AB.
z
eΩ=Ω
GG
Ta coï : 2cos z
OA b e
α
=
JJJGG ⇒
2sin
v( ) 0
0
x
be
A
α
α
−
⎧
⎪
=⎨
⎪
⎩
G
G
0
0
⎧
⎪
Ω=⎨
⎪Ω
⎩
Gcos
sin
0
b
AG b
α
α
−
⎧
⎪
=⎨
⎪
⎩
JJJG ⇒
2sin sin
v( ) cos
0
bb
Gb
α
αα
α
−−Ω
⎧
⎪
=−Ω
⎨
⎪
⎩
G
(2)
So saïnh (1) vaì (2) : z
e
α
Ω=−
GG
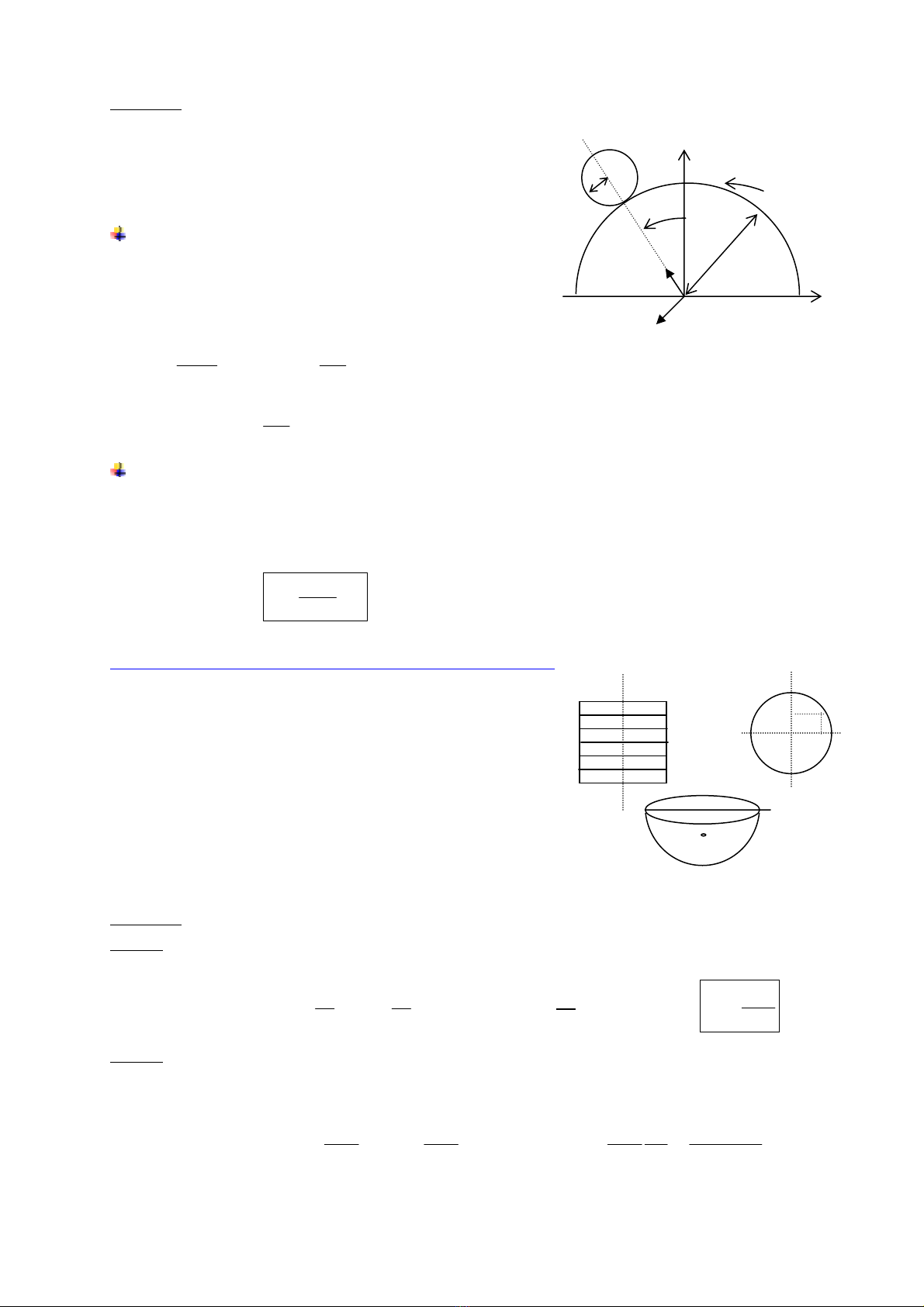
@ AÏp duûng 2 (Trang 30) : Chuyãøn âäüng cuía baïnh xe trãn gêa âåî hçnh truû
Baïnh xe tám C, baïn kênh b làn khäng træåüt trãn giaï âåî hçnh truû tám O, baïn kênh a, cäú âënh
trong hãû quy chiãúu R. Táút caí âãöu nàòm trong màût phàóng thàóng âæïng.
Xaïc âënh veïctå quay Ω
K
cuía baïnh xe theo goïc (, )Oy OC
ϕ
=
J
JK JJKJ .
11
Baìi táûp Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
Baìi giaíi :
(Caïch giaíi : Viãút biãøu thæïc cuía váûn täúc v( )C
G
theo hai
caïch khaïc nhau - âaûo haìm træûc tiãúp vaì bàòng quan hãû váûn
täúc hai âiãøm thuäüc cuìng váût ràõn cáön tim vectå quay - vaì so
saïnh)
y
a
O
C
I
r
e
G
e
ϕ
G
⊕
ϕ
b
Xeït hãû toüa âäü'( , , )
rz
R
eee
ϕ
GGG(hãû toüa âäü R’ quay cuìng våïi
âoaûn OC quanh truûc Oz cuía hãû R(O, x, y, z) våïi vectå
quay bàòng z
e
ϕ
G
). x
Ta coï : OC ⇒
()
r
a b e=+
JJJG G
/
/
v( ) ( ) r
R
R
dOC de
Cab
dt dt
⎛⎞ ⎛⎞
==+
⎜⎟ ⎜⎟
⎝⎠
⎝⎠
JJJG G
G
⇒
/'
v( ) ( ) ( ) 0
r
zr
R
de
Cab ee ab e
dt
ϕ
ϕϕ
⎡⎤
⎛⎞
⎡
⎤
=+ + × =+ +
⎜⎟
⎢⎥
⎣
⎦
⎝⎠
⎣⎦
G
GGGG

v( ) ( )Cabe
⇒
ϕ
ϕ
=
+
G
G
(1)
Goüi IR laì âiãøm cuía baïnh xe truìng våïi âiãøm tiãúp xuïc I. Hai âiãøm C vaì IR thuäüc baïnh xe nãn :
JJ
v( ) v( )
R
CI I=+Ω×C
G
G
GG
Trong âoï : laì vectå quay baïnh xe.
z
eΩ=Ω
GG
Baïnh xe làn khäng træåüt trãn màût âáút nãn : v( ) 0
R
I
=
G
⇒ v( )CICbe
ϕ
=Ω× =Ω
J
JG
G
G
G (2)
So saïnh (1) vaì (2) : z
abe
b
ϕ
+
Ω=
GG
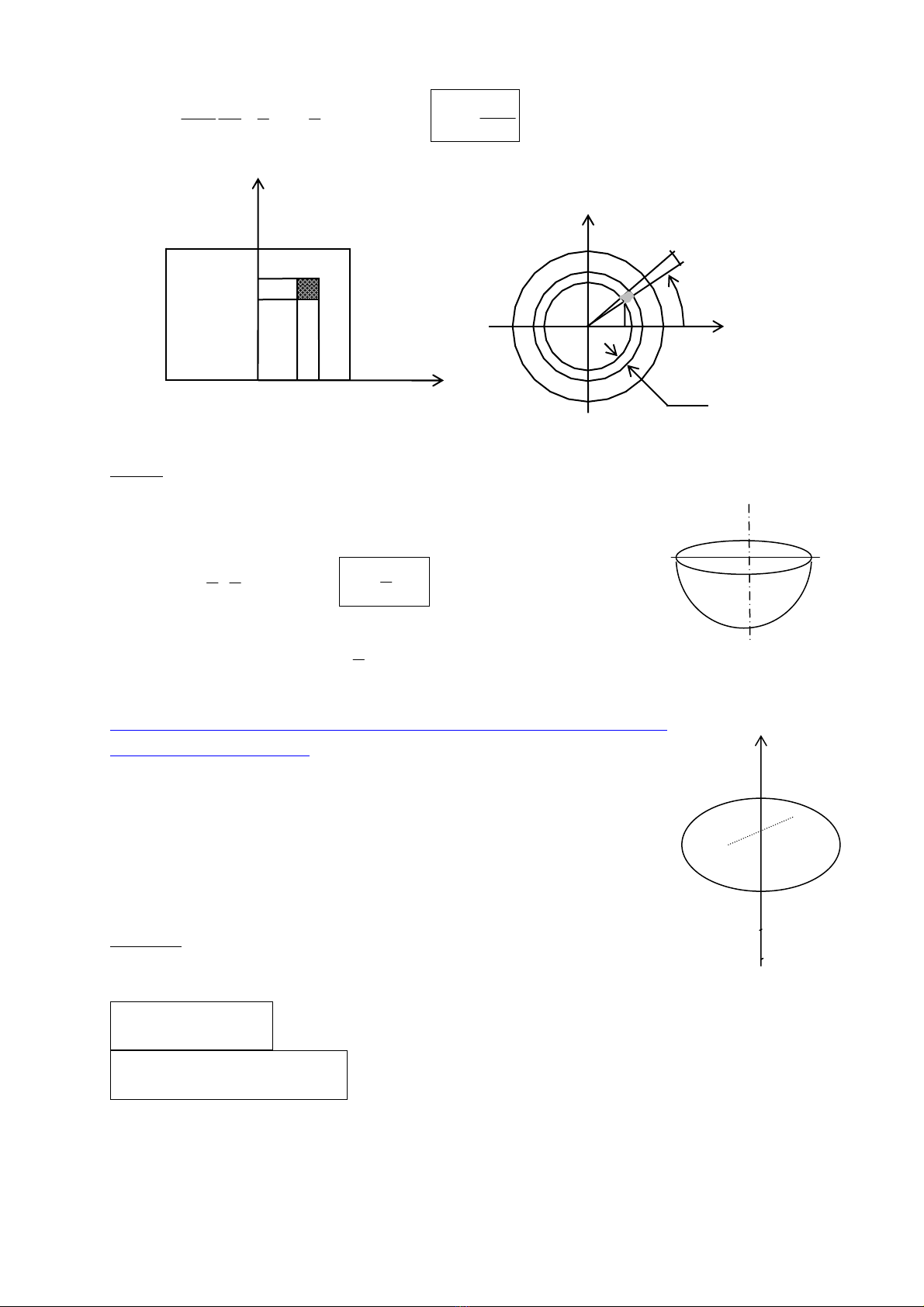
@ AÏp duûng 3 (Trang 34) : Tênh toaïn momen quaïn tênh :
∆
2
∆
1
G H2
H1
∆
A
∆
G
Tênh momen quaïn tênh cuía caïc váût ràõn sau âáy, coï khäúi
læåüng m phán bäú âãöu bãn trong váût ràõn :
1) Momen quaïn tênh âäúi våïi truûc âäúi xæïng ∆ cuía mäüt táúm
phàóng hçnh vuäng caûnh b, bãö daìy khäng âaïng kãø.
2) Momen quaïn tênh âäúi våïi mäüt âæåìng kênh cuía mäüt âéa
troìn baïn kênh R.
3) Momen quaïn tênh âäúi våïi mäüt âæåìng kênh nàòm trong màût
phàóng giåïi haûn baïn cáöu cuía mäüt baïn cáöu baïn kênh R.
Baìi giaíi :
Cáu 1:
Xeït phán täú váût ràõn nàòm taûi toüa âäü x, y coï diãûn têch bàòng dx.dy :
Ta coï : 222
22
() () ()SS S
mm
J r dm dxdy dxdy
xx
bb
∆== =
∫∫ ∫∫ ∫∫ ⇒
/2
2
2
/2 0
bb
b
m
Jdx
x
b
∆
−
=dy
⇒
2
12
mb
J∆=
∫
∫
Cáu 2:
Xeït phán täú váût ràõn coï vë trê xaïc âënh båíi baïn kênh r vaì goïc ϕ, giåïi haûn båíi hçnh vaình khàn (r,
r+dr) vaì chàõn goïc dϕ. Ta coï :
22
4
22 32
22 2
() () 0 0 0
1cos2
( cos ) cos .
42
R
AB
SS
mm mR
J x dm r rd dr r dr d d
RR R
ππ
ϕ
ϕ
ϕϕϕ
ππ π
+
== = =
∫∫ ∫∫ ∫ ∫ ∫
ϕ
12
Baìi táûp Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
⇒
2
4
2
0
11
.sin2
42 2
AB
mR
JR
π
ϕϕ
π
⎡⎤
⎛⎞
=+
⎜⎟
⎢⎥
⎝⎠
⎣⎦
⇒
2
4
AB
mR
J=
-b/2 b/2
b
dy
d
x
y
x
O
y
y
r
A
O
x
B
ϕ
d
ϕ
d
r
x
x
Phán täú dS, khäúi læåüng dm
Cáu 3:
G
Momen quaïn tênh cuía baïn cáöu âäúi våïi mäüt âæåìng kênh ∆ bàòng 1/2
momen quaïn tênh cuía khäúi cáöu âáöy âuí, khäúi læåüng 2m âäúi våïi mäüt
âæåìng kênh ∆ :
(
∆)
2
12
(2 )
25
J
mR
∆
⎡⎤
=⎢⎥
⎣⎦
⇒ 2
2
5
Jm
∆=R
(Ghi chuï : Momen quaïn tênh cuía khäúi cáöu âáöy âuí, khäúi læåüng M âäúi
våïi mäüt âæåìng kênh bàòng : 2
2
5
J
MR
∆=)
@ AÏp duûng 4 (Trang 35) : Træåìng håüp momen âäüng læåüng vaì veïctå
quay song song våïi nhau
(
∆)
z
M ’ M
O
A
Mäüt váût ràõn S quay xung quanh mäüt truûc ∆ song song våïi truûc Oz vaì cäú
âënh trong hãû quy chiãúu R (O; x,y,z) âang xeït, våïi váûn täúc goïc laì
Ω
K
.
Chæïng minh ràòng momen âäüng læåüng
A
L
J
JK cuía váût ràõn S âäúi våïi âiãøm
A cäú âënh trãn ∆ song song våïi nãúu nhæ : Ω
K
∆ laì truûc âäúi xæïng cuía S.
2) S laì mäüt váût ràõn phàóng trong màût phàóng qua A vaì vuäng goïc våïi ∆
Baìi giaíi :
Momen âäüng læåüng âäúi våïi âiãøm A gäöm hai thaình pháön (Xem chæïng
minh åí pháön lyï thuyãút) :
2
//
()
.
A
S
.
L
HM dm=Ω∫∫∫
GG song song våïi vectå quay .
Ω
G
()
.(( .) )
Az
S
L
AM e HM dm
⊥=−Ω∫∫∫ JJJJG JJJJG
GG
vuäng goïc våïi veïctå quay .
Ω
G
Cáön chæïng minh ràòng 0
A
L⊥=
G
.
1) ∆ laì truûc âäúi xæïng cuía váût ràõn (S) :
ÆÏng våïi mäùi âiãøm M thuäüc (S), coï thãø tçm tháúy mäüt âiãøm M’ âäúi xæïng våïi M qua ∆.
Ta coï : '
H
MHM=−
JJJJ JJJG JJG
. vaì .'
zz
A
Me AM e=−
JJJJG JJJJJG
GG ) ⇒ (.) '( '.
zz
H
MAMe HM AMe=−
J
JJJG JJJJG JJJJ JJJJJG JG
G
G
13
Baìi táûp Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
⇒ ⇒ 0
A
L⊥=
G
//
A
Az
LL J Je
∆∆
==Ω=Ω
GG G G
2) (S) laì váût ràõn phàóng trong màût phàóng qua A vaì vuäng goïc våïi
∆
:
Våïi moüi âiãøm M thuäüc váût ràõn (S), ta coï : .
z
AM e 0
=
J
JJJG
G
båíi vç z
A
Me
⊥
J
JJJG
G
⇒ 0
A
L⊥=
G
@ BAÌI TÁÛP COÏ GIAÍI (Trang 41) : Con làõc keïp
Mäüt con làõc keïp gäöm hai thanh OA vaì AB giäúng nhau, âäöng
cháút, khäúi læåüng m, chiãöu daìi 2b vaì âæåüc näúi nhau bàòng khåïp
quay taûi A. Hai thanh cuìng chuyãøn âäüng trong màût phàóng thàóng
âæïng (Oxy) vaì goïc nghiãng cuía noï âæåüc xaïc âënh bàòng caïc goïc α
vaì β so våïi truûc (Ox) thàóng âæïng hæåïng xuäúng.
y
B
A
β
α
G1
G2
O
Tênh momen âäüng læåüng âäúi våïi âiãøm O vaì âäüng nàng cuía con
làõc keïp. Nhàõc laûi ràòng momen quaïn tênh cuía mäüt thanh coï chiãöu
daìi 2b âäúi våïi trung âiãøm : x
Baìi giaíi :
Momen âäüng læåüng âäúi våïi âiãøm O :
OA quay quanh truûc Oz cäú âënh, (S) váût ràõn phàóng nàòm trong màût phàóng qua O vaì vuäng
goïc våïi truûc Oz, ta coï :
1
() ()
OOz
LOA J OAe=Ω
GG
z
Våïi : 1
α
Ω= vaì
222
14
() () 33
Oz Gz
J OA J OA mb mb mb mb=+=+=
2
⇒ 2
4
()
3
Oz
L
OA mb e
α
=
G
G
(Ghi chuï : træåìng håüp váût ràõn phàóng quay quang truûc () vuäng goïc våïi màût phàóng cuía váût
ràõn : G)
() ()
OO
LOA L OA
⊥
=G
Vaì : 2
1
() ()
2
KOz
EOA J OA
α
= ⇒ 22
2
()
3
K
EOA mb
α
=
Âënh lyï Koenig cho ta :
*
222 222
1
() () () () ()
2
OG Gzz
L
AB OG mv G L AB OG mv G J AB e
β
=× + =× +
JJJJG JJJJG
GG
GGG
2* 2
22
111
() v() () v() ()
222
KK G
EAB m G EAB m G J AB2
2z
β
=+=+
Våïi : 2
2cos cos
2sin sin
0
bb
OG b b
α
β
α
β
+
⎧
⎪
=+
⎨
⎪
⎩
JJJJG ⇒ v( 2
2sin sin
) 2 cos cos
0
bb
Gb b
α
αββ
α
αβ β
⎧−−
⎪
=+
⎨
⎪
⎩
G
2
2
1
() 3
Gz
JABJ mb==
⇒ 22
1
() (4 )2( )cos( )
3
O z
L
AB mb mb e
αβ αβ αβ β
⎡⎤
=+++−+
⎢⎥
⎣⎦
G
G


(Læu yï : cos( ) cos .cos . sin .sin
α
βαβα
−= +
β
)
O
)
Suy ra :
()()(
OO
L conlackep L OA L OB=+
GGG
14
Baìi táûp Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
⇒ 216 4
( ) 2( ) cos( )
33
O z
L
conlackep mb e
αβαβ αβ
⎡⎤
=+++−
⎢⎥
⎣⎦
G
G


Ta coï : 222222
2
v( ) 4 4 cos( )Gb b b
α
βαβα
=++ −


β
⇒ 22 22 2 2
2
11
() 4 4 cos( ) ()
22
KGz
EAB mb b b J AB
α
βαβαβ
⎡⎤
=++ −+
⎣⎦


β
⇒ 222 2
11
() 4 4cos( )
26
K
EAB mb mb2
α
βαβαβ β
⎡⎤
=++−+
⎣⎦


)
K
Toïm laûi :
()()(
KK
E conlackep E OA E AB
=
+
⇒ 22 2
82
() 2)cos(
33
K
E conlackep mb )
α
βαβ αβ
⎡⎤
=++ −
⎢⎥
⎣⎦


BAÌI TÁÛP COÏ HÆÅÏNG DÁÙN :
@ Baìi 1 (Trang 42) : Momen quaïn tênh cuía mäüt baïn cáöu
Momen quaïn tênh cuía mäüt baïn cáöu âäúi våïi âæåìng kênh ∆ cuía noï
bàòng : 2
2.
5
J
mR=. Haîy tênh momen quaïn tênh J ’ cuía baïn cáöu âäúi
våïi truûc ∆‘ âi qua âènh S vaì song song våïi ∆. Khoaíng caïch tæì khäúi
tám G âãún tám C cuía quaí cáöu bàòng 3
8
CG R=.
Baìi giaíi :
Âënh lyï Huyghens :
222
)'() ()(
G
J
JmSG JmCG mSG
∆∆
⎡⎤
=+ =− +
⎣⎦ 22
35
'()(
88
)
J
Jm R m R=− + ⇒ 2
13
'20
Jm=R
Baìi 2 (Trang 42) :Momen âäüng læåüng cuía mäüt con làõc @
öng Mäüt con làõc OABC hçnh chæî T (tiãút diãûn khäng âaïng kãø), âä
cháút, mäüt âáöu âæåüc treo åí âáöu O vaì coï thãø dao âäüng xung quanh
trong màût phàóng thàóng âæïng mäüt truûc ∆ nàòm ngang. Xaïc âënh
momen âäüng læåüng âäúi våïi âiãøm O theo váûn täúc goïc
θ
cuía con làõc.
Biãút : OA = 2AB = 2AC = b, OA vaì OB coï cuìng khä læåüng. Nhàõc
laûi ràòng momen quaïn tênh cuía mäüt thanh coï chiãöu daìi b âäúi våïi
trung âiãøm cuía noï laì :
úi
2
1.
12
Jmb=
Baìi giaíi :
OABC laì v
GGáût ràõn phàóng nàòm trong màût phàóng qua O vaì vuäng goïc våïi truûc quay A :
Oz
LJe
∆
=Ω våïi : z
e
θ
Ω= G
⇒ Oz
LJe
θ
∆
=
G
G
22 22
() ( mb
J⎡
⎢
)212 212
mb mb mb
JJOA BC
∆∆ ∆
⎡⎤
=+=+++
⎢⎥ ⎥
⎣⎦⎣⎦
⇒
⎤2
17
12
mb
J∆=
Toïm laûi :
2
17
12
Oz
mb
L
e
θ
=
GG
@ Baìi 3 (Trang 42) : Âäüng nàng cuía mäüt chiãúc âu :
O
B
C
A
∆
θ
z
e
G
∆
’
∆
G
∆
G
S
C
15