Baìi táûp Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
BAÌI TÁÛP CHÆÅNG 2
TIÃÚP XUÏC GIÆÎA HAI VÁÛT RÀÕN-ÂËNH LUÁÛT VÃÖ MA SAÏT
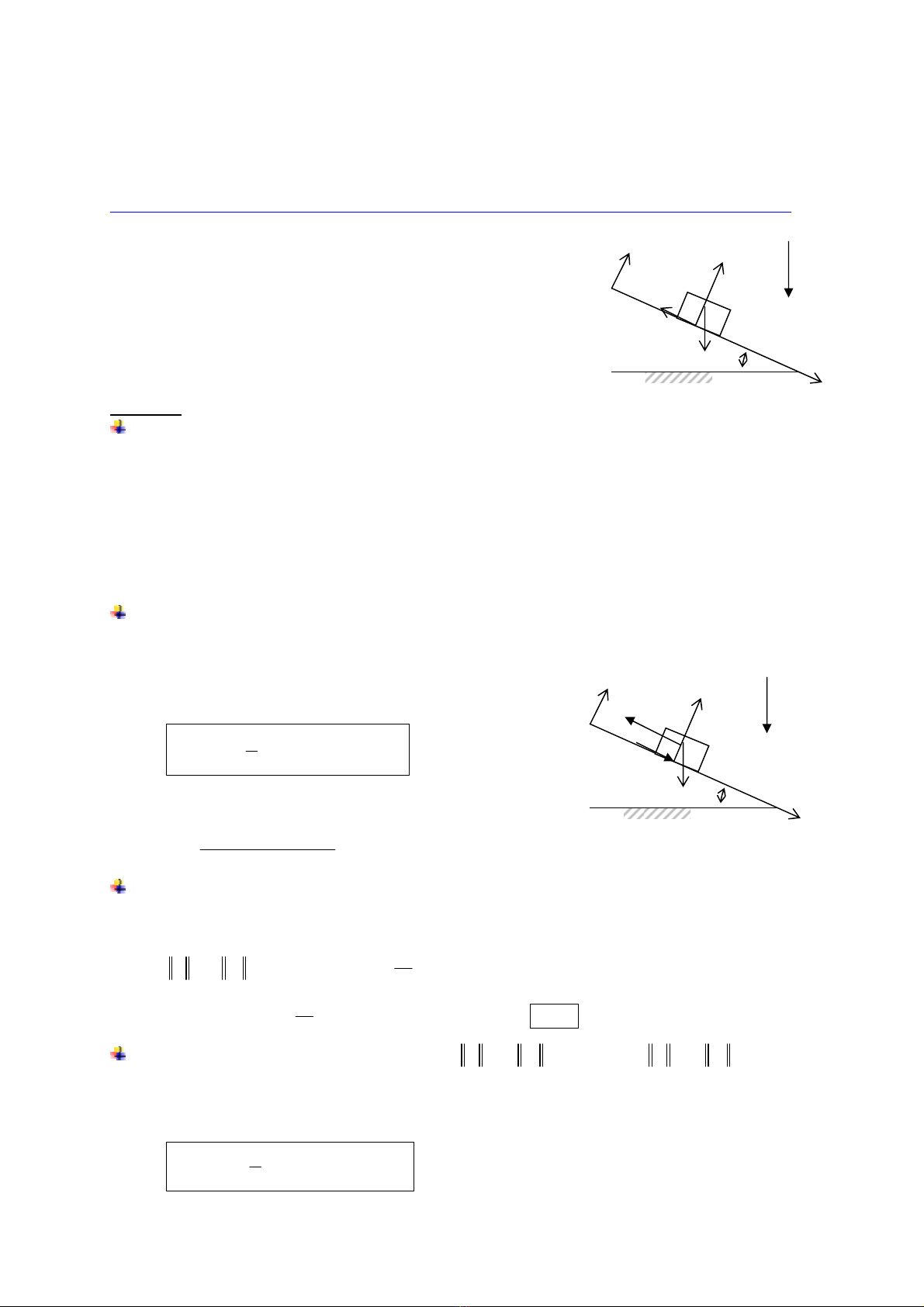
@ AÏp duûng 1: (Trang 98) Chuyãøn âäüng cuía hçnh láûp phæång trãn màût phàóng nghiãng:
Mäüt hçnh láûp phæång khäúi læåüng m âæåüc háút lãn våïi váûn täúc
ban âáöu v0 (v0 > 0), doüc theo âæåìng däúc chênh cuía mäüt màût
phàóng nghiãng mäüt goïc α so våïi màût phàóng ngang. g
N
T
mg
α
C
x
y
O
Xaïc âënh chuyãøn âäüng cuía hçnh láûp phæång naìy (chuyãøn
âäüng tënh tiãún doüc theo âæåìng däúc chênh (Ox) cuía màût phàóng
nghiãng) theo caïc giaï trë khaïc nhau cuía v0. Cho biãút hãû säú ma
saït træåüt giæîa khäúi vuäng vaì màût phàóng nghiãng laì f.
Bài giải :
Ngoại lực tác dụng lên vật rắn bao gồm : Trọng lượng mg
, Tác động cơ lên khối vuông
tại chỗ tiếp xúc : . xy
R
Te Ne=+
 
với T và N là giá trị đại số : N > 0. (Vật rắn chuyển động tịnh
tiến, nên ma sát lăn và ma sát xoay không xuất hiện).
Áp dụng định lý về động lượng ( ( ) ei
i
PmaG F==
∑

) ⇒ ()ma G mg T N
=
++

Chiếu lên Ox và Oy:
sin (1)
0cos
mx mg T
mg N
α
α
=+
⎧
⎨=− +
⎩

(2)
Lúc đầu, khối vuông đi lên trên mặt phẳng nghiêng, T
hướng xuống dưới : T > 0 và T =
f.N
Từ (2) suy ra : N = mgcosα ⇒ .cosTfNmgf
α
==
g
N
T
mg
C
α
0
v
x
y
O
Thay vào (1) ta có : (sin cos )xg f
α
α
=+

⇒ 0(sin cos )vgft
ν
αα
=− + +
⇒ 2
0
1(sin cos )
2
x
tg f t
ν
αα
=− + +
(Ghi chú : Điều kiện ban đầu: t = 0 ⇒0
0;xx
ν
=
=−
)
Vận tốc khối vuông bằng 0 tại thời điểm t0 với :
)cos(sin
0
0
αα
ν
fg
t+
=
Tại t = t0, khối vuông dừng lại và có xu hướng chuyển động đi xuống trên mặt phẳng
nghiêng nên hướng lên trên : T < 0. Kể từ thời điểm t = tT0, khối vuông vẫn đứng yên, nếu
như:
NfT ≤ hay TfN
−
≤ ⇒ T
f
N
−
≤
Từ (1) và (2) suy ra : Ttg
N
α
−= ⇒ tg f tg
α
ϕ
≤
= ⇒
ϕ
α
≤
Ngược lại, nếu
α
ϕ
> hay tg f
> thì : TfN= (bởi vì nếu TfN<, ta sẽ suy
ngược lại rằng
α
ϕ
< , điều này trái với giả thiết) Tf
⇒.cosNfmg
α
=
−=−
Từ (1) suy ra gia tốc của khối của khối vuông :
)cos(sin
α
α
fgx −=
⇒ 2
0)cos(sin
2
1
)( tfgtxx
αα
−+= : Khối vuông chuyển động đi xuống nhanh dần đều.
22
Baìi táûp Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
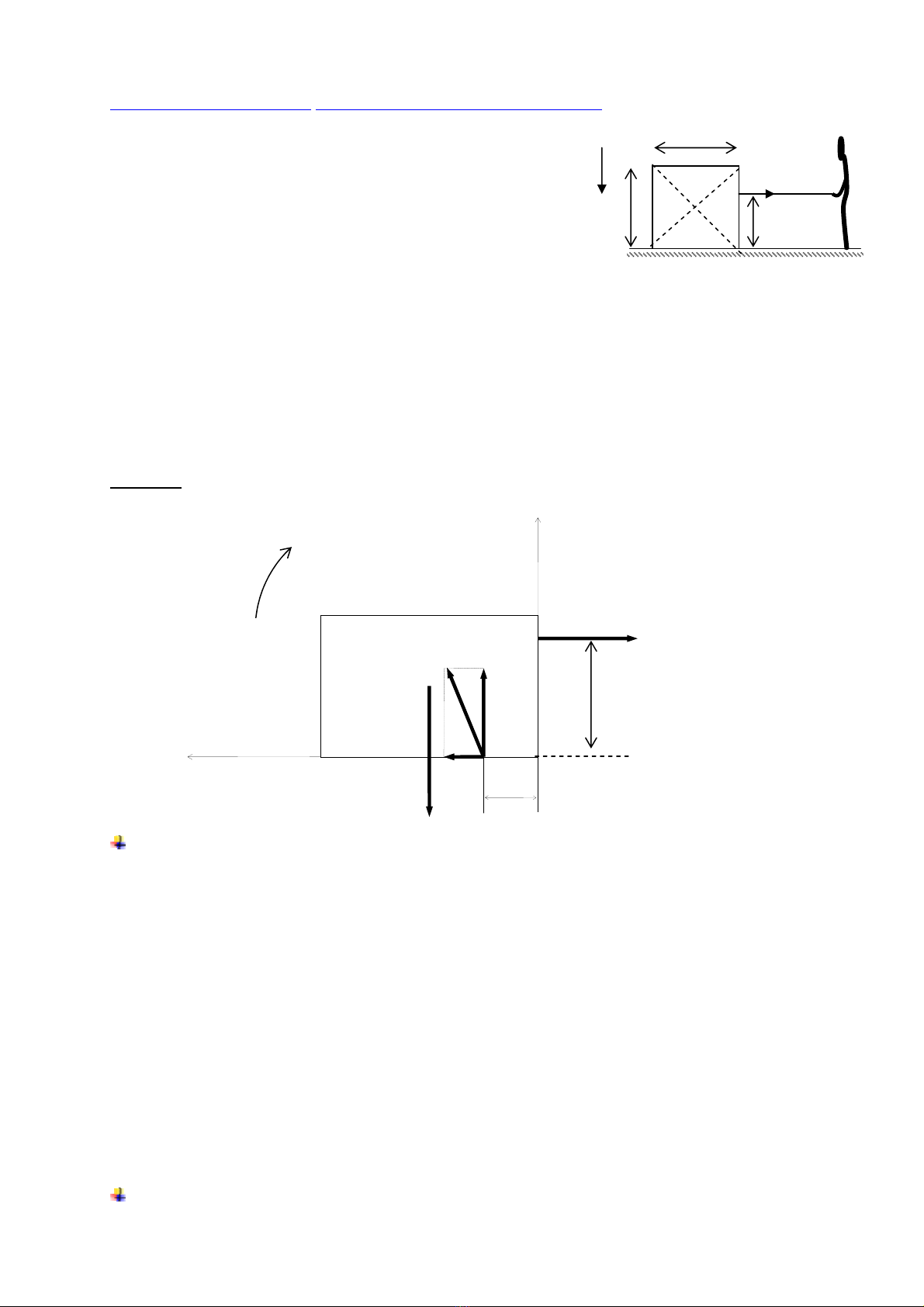
@ AÏp duûng 2: (Trang 99) Cán bàòng cuía váût ràõn trãn màût âáút :
Mäüt váût ràõn âäöng cháút, coï daûng hçnh khäúi chæî nháût, caïc caûnh
laì 2a vaì 2b, khäúi læåüng m, khäúi tám G, nàòm yãn trãn màût âáút
nàòm ngang. Mäüt ngæåìi muäún dëch chuyãøn váût ràõn bàòng caïch
keïo mäüt såüi dáy (buäüc taûi mäüt âiãøm H trãn váût ràõn vaì nàòm
trong màût phàóng trung bçnh âi qua khäúi tám G sao cho OH =
h) taïc duûng lãn váût ràõn mäüt læûc F nàòm ngang. Hãû säú ma saït
træåüt giæîa màût âáút vaì váût ràõn laì f.
H
2a
h
G
2b
F
O
g
Ngæåìi keïo khäng keïo âuí maûnh vaì váût ràõn váùn âæïng yãn.
Chæïng minh ràòng caïc taïc âäüng cå tiãúp xuïc giæîa váût ràõn vaì màût âáút suy biãún thaình mäüt læûc R
taïc duûng lãn âiãøm mäüt I (thuäüc màût phàóng trung bçnh cuía váût ràõn) nàòm trãn màût phàóng tiãúp xuïc
giæîa màût âáút vaì váût ràõn).
Cæåìng âäü cuía læûc F phaíi thoía maîn nhæîng âiãöu kiãûn naìo âãø váût ràõn thæûc sæû âæïng yãn trãn màût
âáút ?
Bài giải :
⊕
F
mg
N
T
I
H
2
a
R
2b h
O
x
x
y
Vì bề mặt tiếp xúc giữa mặt đất và vật rắn là lớn Không thể bỏ qua ma sát lăn và xoay.
Tác động cơ tại chỗ tiếp xúc giữa vật ắn và mặt đất khi thu gọn về điểm tiếp xúc I nào đó
thuộc mặt phẳng trung bình bao gồm :
⇒
r
.xy
R
Te Ne=+
và ,I tiepxuc
M
(N > 0, T > 0)
Ngoại lực tác dụng lên khối vuông bao gồm : Trọng lượng mg
, lực kéo , tác động cơ tại
điểm tiếp xúc I :
F
.xy
R
Te Ne=+
 
và .
,I tiepxuc
M
Khi vật rắn cân bằng, ta có :
+ Tổng các ngoại lực tác dụng lên vật rắn bằng 0 :
0NTmgF++ + =

(1) ⇒Nmg
TF
=
⎧
⎨=
⎩
Trong đó : T
fN≤⇒FfNfmg≤=
+ Momen các ngoại lực tác động lên khối vuông đối với điểm I bằng 0 :
 

,
()
I tiepxuc
IG mg IH F II T N M×+×+×++ =0
0⇒ (2)
,
()
zItiepxuc
amg hF xN e M−++ + =
Để hệ lực suy biến thành một lực
,
(, )
I tiepxuc
RM

R
thì phải có : ,0
I tiepxuc
M=
23
Baìi táûp Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
Với và , từ (2) suy ra : ()Nmg=,0
I tiepxuc
M=
0xamghF
−
+=
⇒ h
mg
F
ax −=
⇒ Tác động cơ tại chỗ tiếp xúc, khi thu gọn về điểm tiếp xúc I có tọa độ h
mg
F
ax −= sẽ suy
biến thành một lực là
R
.
Để I có tọa độ h
mg
F
ax −= thuộc bề mặt tiếp xúc thì phải có : ax 20 ≤
≤
. Bất đẳng thức
trên thỏa mãn khi 0
F
ah
mg
−≥ hay mga
Fh
≤
Tóm lại : Với h
mga
F≤, tác động cơ tiếp xúc từ mặt đất lên vật rắn suy biến thành một lực
đặt tại điểm I có tọa độ
RNT=+

h
mg
F
ax −= và thuộc bề mặt tiếp xúc.
(Ghi chú :
+ Trường hợp giới hạn : T = fN ⇒ F = fN = fmg ⇒
f
mg
x
ah
mg
=− ⇒
x
afh=− ⇒ điểm I
nằm tại có tọa độ x0 : 0
x
afh=− . Trường hợp TfN
≤
thì FfNfmg
≤
=⇒ 0
x
x≥⇒ điểm
I nằm trong khoảng I0A.
⊕
F
mg
N
T
QI0
H
2b
2
a
R
G
P
h
O
x
0
x
y
+ Gọi P là giao điểm của và F

mg
: Ta
có : 000
.
I
QOQQI ax fh
(3)
(4)
(1)
mga
Fh
=
F
fmg=
(2)
fmg
2b
h
F
tgh
ϕ
=−=− ==
⇒0
(,)tg PI PQ tg
ϕ
=
  ⇒0
(,)PI PQ
ϕ
=
  .
Mặt khác, trong trường hợp giới hạn
(, ) FfN
tg R N f tg
NN
ϕ
== ==
 ⇒
R
 nằm
trên phương PIo hay nói khác đi
R
 đi qua
điểm P).
Để khối vuông thực sự đứng yên trên
mặt đất, phải có điều kiện :
+ Khối vuông không trượt so với mặt đất :
FT fN fmg=≤ = ⇒fmgF ≤ (3)
+ Khối vuông không lật quanh cạnh qua O,
nghĩa là nó còn cân bằng và liên kết của nó
24
Baìi táûp Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
với mặt đất vẫn tồn tại (tức là áp lực N vẫn tồn tại : hay
0N≥()0
O
MN≥
).
Suy ra :
()( ) ()
()0
ext
Oi z O
i
O
MF Fhmgae MN
MN
⎧=− + =
⎪
⎨
⎪≥
⎩
∑

0
⇒ 0Fh mga−≤
⇒h
mga
F≤ (4)
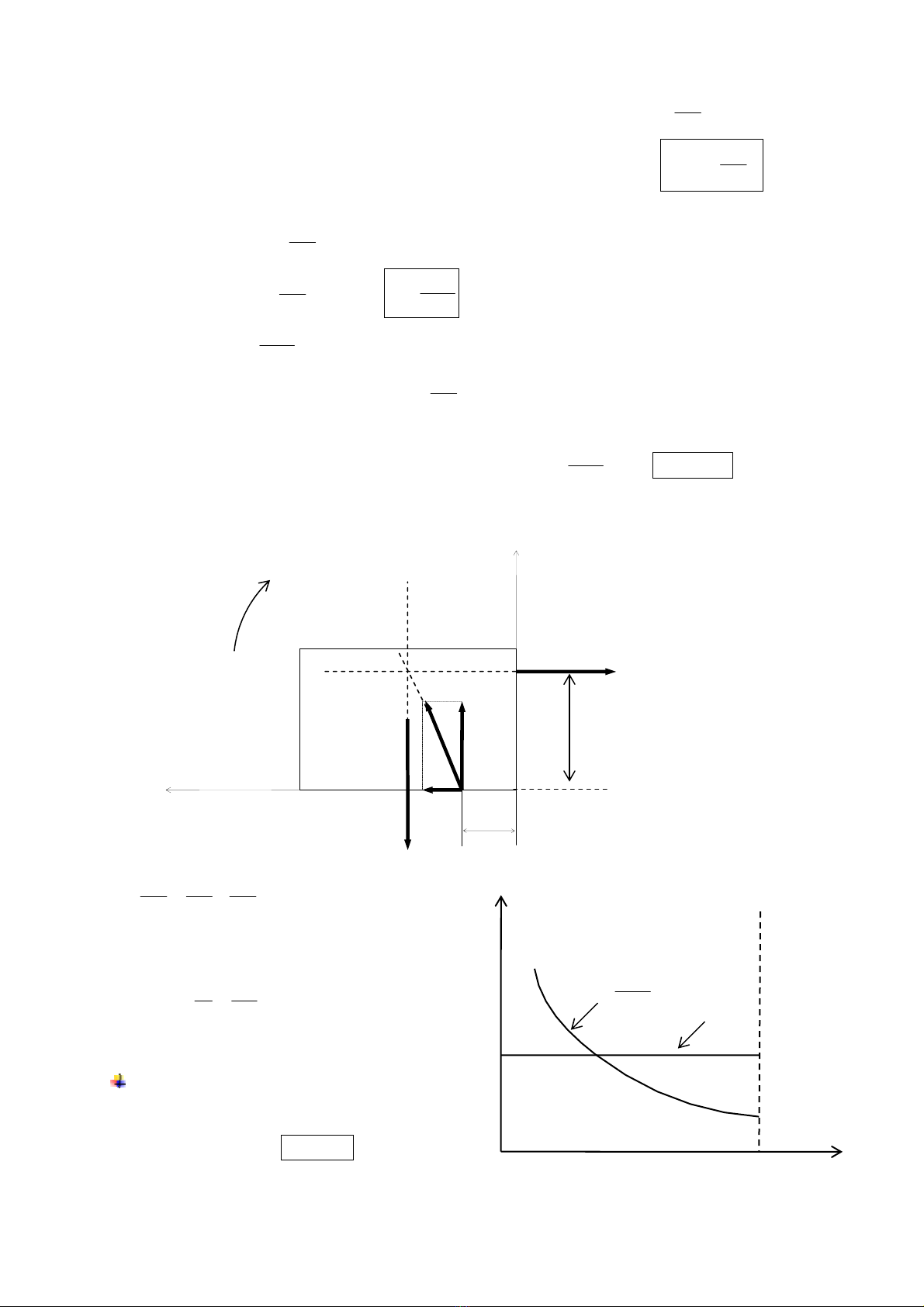
Hệ hai bất đẳng thức trên có thể giải bằng đồ thị như trên hình vẽ : Vùng (1) : Vật rắn trượt
không lật trên mặt đất.Vùng (2) : Vật rắn vừa trượt vừa lật trên mặt đất.
Vùng (3) : Vật rắn không trượt, chỉ lật trên mặt đất.
Vùng (4) : Vật rắn không trượt không lật trên mặt đất (vật rắn thực sự cân bằng )
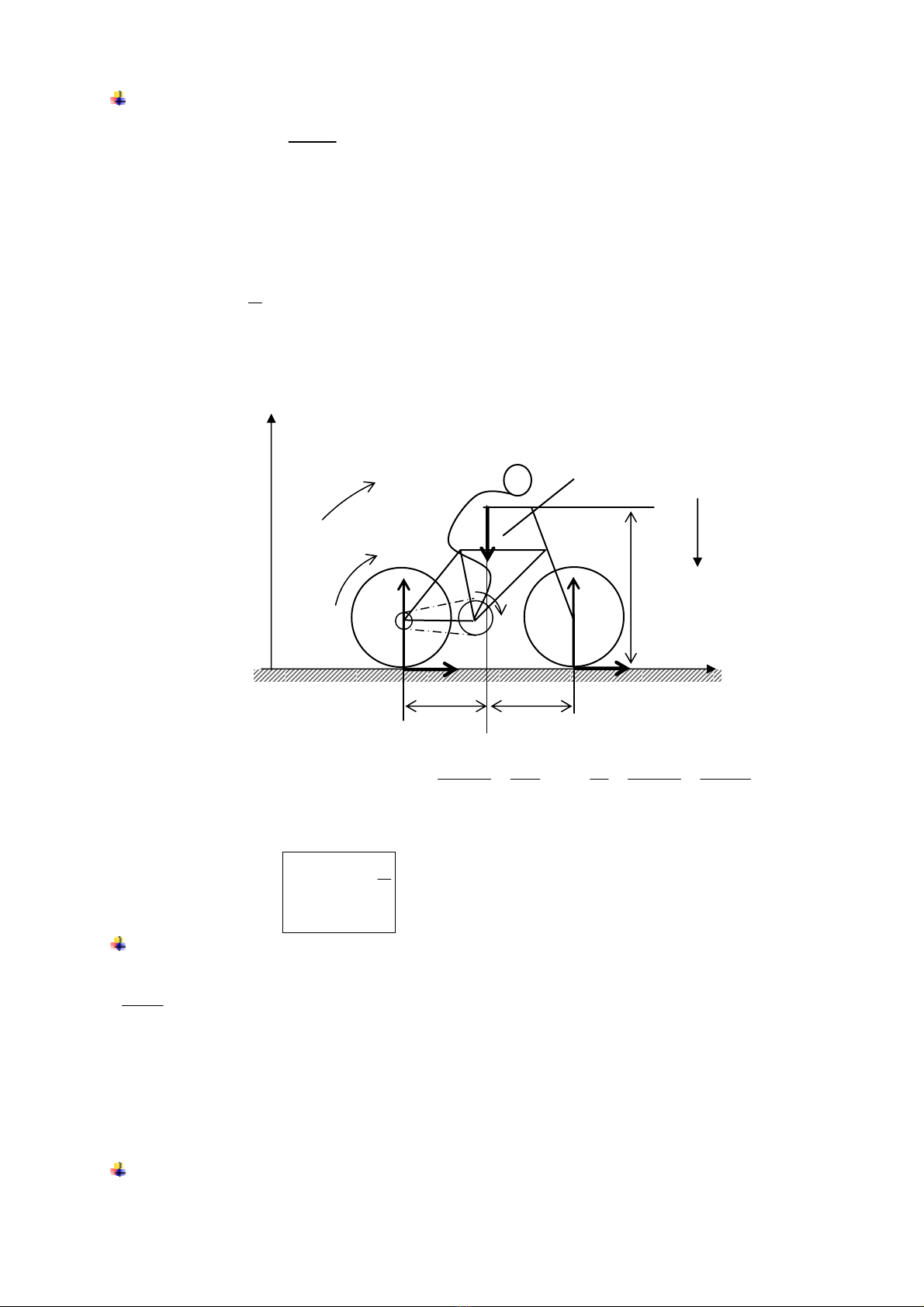
@ AÏp duûng 3: (Trang 101): Khåíi âäüng cuía ngæåìi âi xe âaûp:
Mäüt ngæåìi âi xe âaûp khåíi âäüng trãn mäüt màût âæåìng nàòm ngang: Hãû quy chiãúu traïi âáút âæåüc
xem laì Galileïe. Ngæåìi âi xe âaûp âæåüc xem nhæ laì
mäüt váût ràõn gàõn liãön våïi xe âaûp (boí qua khäúi læåüng
cuía âäi chán âang chuyãøn âäüng). Goüi m laì täøng
khäúi læåüng cuía ngæåìi vaì xe âaûp. Hai baïnh xe laì
giäúng nhau, coï baïn kênh R vaì coï khäúi læåüng khäng
âaïng kãø. Khäúi tám G cuía hãû ngæåìi-xe âæåüc xaïc
âënh båïi caïc khoaíng caïch a, b vaì h. Goüi f laì hãû säú
ma saït giæîa caïc baïnh xe vaì màût âáút (boí qua caïc ma
saït khaïc) vaì n laì tè säú giæîa säú ràng (nombre de
dents) cuía âéa xêch vaì cuía lêp (roue-libre) åï baïnh
sau.
g
G
b
a
yO
⊗
⊕
x
h
z
Momen Γ cuía ngáùu læûc maì ngæåìi âi xe taïc âäüng vaìo âéa xêch phaíi bàòng bao nhiãu âãø caïc baïnh
xe khäng bë træåüt trãn màût âáút ?
Baìi giaíi :
Phản lực của mặt đất tác dụng lên mỗi bánh xe:
.
K
Kx Ky
R
Te Ne=+

Với : ; T
0; 1, 2
K
Nk>= K là giá trị đại số (bỏ qua các ma sát khác).
Để bánh xe không trượt trên mặt đất, phải có : k
TfN≤k
(1)
Ta cần xác định T1, T2, N1, N2 và thay vào biểu thức (1), từ đó sẽ có kết luận.
Xét cơ hệ gồm người + xe. Ngoại lực tác dụng lên hệ : Trọng lượng , các áp lực và lực
ma sát từ mặt đất tác dụng lên hai bánh xe : TT
mg
12 1 2
,, ,N N

.
Áp dụng định lý về động lượng cho hệ người + xe đạp ( () k
i
i
dP ma G F
dt ==
∑
)
⇒
12 1 2
()ma G T T N N mg=++ + +


Chiếu lên hai trục x và z : 12
12
0
mx T T
NNmg
=+
⎧
⎨=+−
⎩
 (2)
25
Baìi táûp Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
Áp dụng định lý về momen động lượng đối với khối tâm CK của mỗi bánh xe, trong hệ
quy chiếu khối tâm : ext
/*
*(
K
K
C
Ci
i
R
dL MF
dt
⎛⎞
=
⎜⎟
⎜⎟
⎝⎠
∑
)
với : *
*v
K
CKiii
i
LCMm0
=
×=
∑
(vì bỏ qua
khối lượng của các bánh xe)
⇒2
1
0'
0
TR
TR
=− +Γ
⎧
⎨=−
⎩ ⇒2
1
0'
0
TR
T
=− +Γ
⎧
⎨=
⎩
Trong đó Γ’ là momen tác động lên bánh sau, tạo nên bởi momen Γ do người đi xe tác động
lên bàn đạp : 'n
Γ
Γ=
g
b
a
G
y O
⊗
⊕
mg
C2C1
'
Γ
Γ
1
T
2
T
2
N
1
N
z
x
h
(Ghi chú : Lực căng trên dây xích :
dia xich lip
22'
DD
t
F
Γ
Γ
==
⇒ dia xich dia xich
lip lip
D
'D
Zn
Z
=
==
Γ với
Ddia xich, Dlip lần lượt lừ đường kính của đĩa xích và của líp; Zdia xich, Zlip lần lượt là số răng của
đĩa xích và của líp).
⇒2
1
0
0
TR n
T
Γ
⎧=− +
⎪
⎨
⎪=
⎩
(3)
Áp dụng định lý về momen động lượng đối với khối tâm G của hệ người + xe, trong hệ
quy chiếu khối tâm :
ext
/*
*(
G
Gi
i
R
dL MF
dt
⎛⎞
=
⎜⎟
⎝⎠
∑
)
 0
với : **( )*( )
GG G
L L nguoi khungxe L cacbanhxe
=
++
 =
(Ghi chú : Do người + khung xe chuyển động tịnh tiến so với mặt đất, nên sẽ cố định trong
hệ quy chiếu khối tâm, do đó : *( ) 0
G
L nguoi khungxe
+
=
. Mặc khác, do bỏ qua khối lượng
các bánh xe nên : *
*( ) v 0
Gi
i
L cacbanhxe GM m=×
ii
=
∑

).
(4) ⇒22 1
0Nb Th Na=−−
Giải hệ phương trình (2), (3) và (4) :
Từ (2), suy ra : 12
- NmgN=
26