Bµi tËp lín: LT§KT§
Sinh viªn : Tạ Văn Tiến_
DHDI7TH
1
bµi tËp lín lý thuyÕt ®iÒu khiÓn tù ®éng
§Ò bµi :
Cho hÖ thèng ®iÒu khiÓn tèc ®é ®éng c¬ nh- h×nh vÏ :(h×nh 1)
Yªu cÇu :
1. X©y dùng s¬ ®å khèi cÊu tróc vµ hµm truyÒn ®¹t c¸c phÇn tö
2. XÐt æn ®Þnh hÖ thèng vµ tÝnh qu¸ tr×nh qu¸ ®é (b»ng ph- ¬ng ph¸p sè Tustin) khi bá
qua kh©u PID vµ ng¾t bá kh©u W4(p) .
3. Khi cã bé PID , cã W4(p) xÐt æn ®Þnh hÖ thèng b»ng Matlab, cô thÓ :
a, c¾t bá W4(p) t×m c¸c tham sè cña bé PID ®Ó smax <=15% .
b,bá PID , gi÷ l¹i W4(p) t×m Td ®Ó chÊt l- îng hÖ thèng t- ¬ng ®èi tèt .
c, cã PID , cã W4(p) x¸c ®Þnh c¸c tham sè ®Ó smax <=10% .
- nhãm 13 cã c¸c sè liÖu :
R =10 K , R1 =145 K , C1 = 26mF
Hµm truyÒn ®¹t ®éng c¬: 1.. 2++
=pTpTT
k
W
mem
m
dc víi km = 6,5 ; Tm = 0,3 sec ; Te =
0,15 sec ta cã : 13,0045,0
5,6
2++
=pp
Wdc =W3(p)
- Kh©u K§1 cã hµm truyÒn nh- sau :
W1(p) = 177,3
5,14
1
1
1
+
=
+ppT
K
- 101,0
25
)(
2+
=p
pW
Bµi lµm
1. X©y dùng s¬ ®å cÊu tróc hÖ thèng :
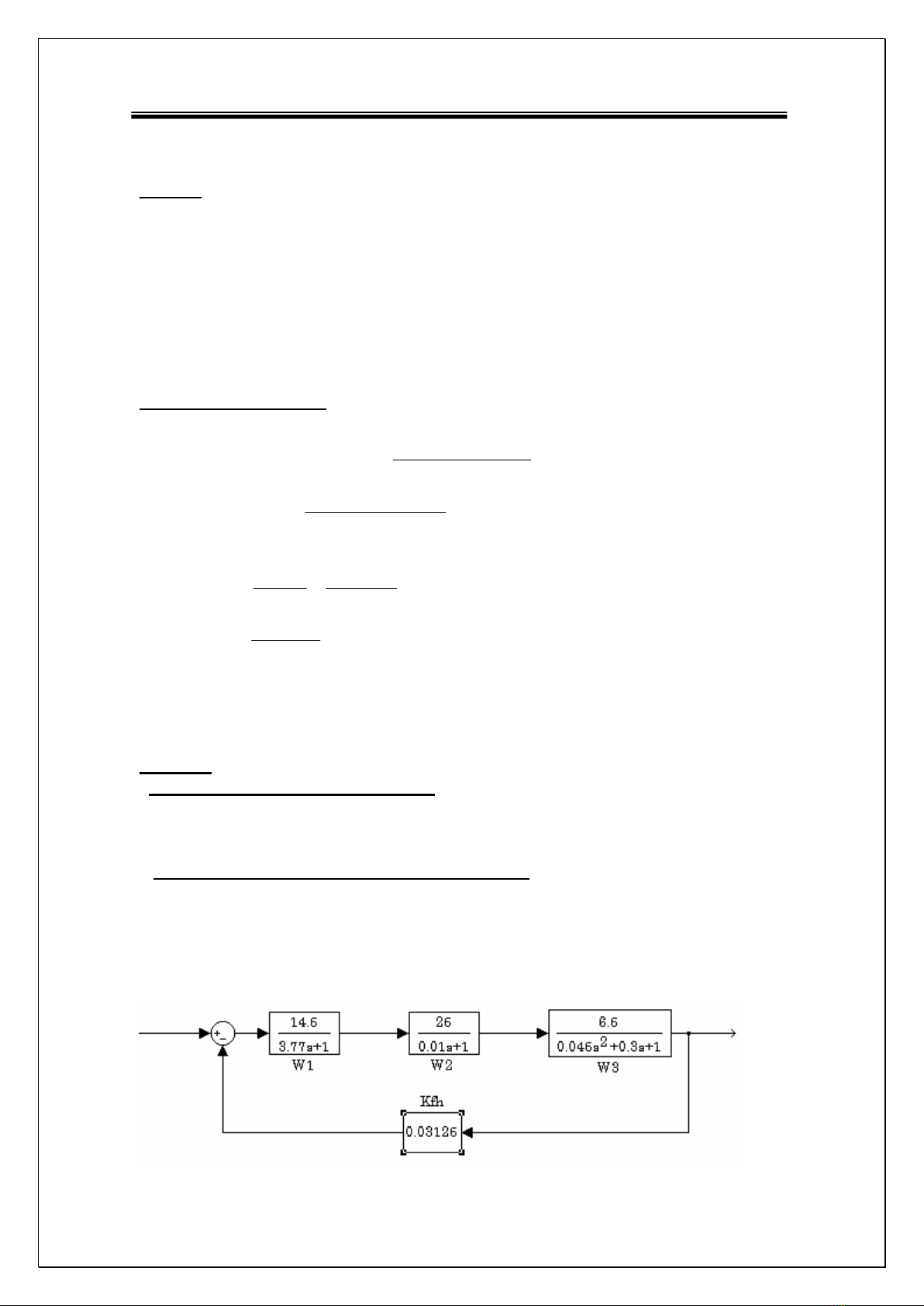
- s¬ ®å cÊu tróc hÖ thèng ®- îc vÏ nh- h×nh sè 2 trong ®ã c¸c hµm truyÒn ®¹t ®·
®- îc tÝnh vµ hÖ sè ph¶n håi Kf = KpaKft =0,125*0,25 = 0.03125
+ nguyªn lý lµm viÖc cña hÖ thèng :
2.XÐt æn ®Þnh hÖ thèng vµ tÝnh qu¸ tr×nh qu¸ ®é :
- khi bá kh©u PID vµ ng¾t bá W4(p) ta cã s¬ ®å cÊu tróc nh- sau :
(H×nh vÏ sè 3)
Bµi tËp lín: LT§KT§
Sinh viªn : Tạ Văn Tiến_
DHDI7TH
2
HÖ thèng gåm hai kh©u qu¸n tÝnh vµ mét kh©u dao ®éng m¹ch ph¶n håi cã hÖ sè b»ng
0.03125 .
- xÐt kh©u qu¸n tÝnh : W1(p)= )(
)(
177,3
5,14 1
pE
pY
p=
+
thÕ p =
1
12
+
-
Z
Z
T
vµo ta cã : )(.)(..)(.)(. 11111 ZEBZEZBZYAZYZ ++=
trong ®ã :
T
T
B
T
T
A
+
=
+
-
=
54,7
5,14
54,7
54,7
1
1
Ph- ¬ng tr×nh sai ph©n cã d¹ng :
][]1[][]1[ 11111 kEBkEBkYAkY +++=+
- t- ¬ng tù xÐt víi kh©u qu¸n tÝnh : 101.0
25
)(
2+
=p
pW = )(
)(
1
2
pY
pY thay p =
1
12
+
-
Z
Z
T
vµo
ta cã:
)(.)(..)(.)(. 1112222 ZYBZYZBZYAZYZ ++= (1)
trong ®ã :
T
T
B
T
T
A
+
=
+
-
=
02
0
.25
02.0
02.0
2
2
Ph- ¬ng tr×nh sai ph©n cã d¹ng :
][]1[][]1[ 1212222 kYBkYBkYAkY +++=+ (2)
§èi víi kh©u dao ®éng : )(
)(
13.0045.0
5.6
)(
2
2
3pY
pY
pp
pW =
++
= ta cã :
Thay p =
1
12
+
-
Z
Z
T
vµo :
( )
33
2
3
22
3
2
3
1.2.5.6
)(
1
1
1
.
2
.3.0)
1
1
.
2
(045.0
5.6
)(
CZBZA
ZZT
ZW
Z
Z
TZ
Z
T
ZW
++
++
=Þ
+
+
-
+
+
-
=
Trong ®ã :
TTC
TB
TTA
6.018.0
36.02
6.018.0
2
3
2
3
2
3
-+=
-=
++=
Ph- ¬ng tr×nh ®¹i sè :
)()(.2)([5.6)()().(. 222
22
33
2
3ZYZZYZYZTZYCZZYBZZYA ++=++
Ph- ¬ng tr×nh sai ph©n t- ¬ng ®- ¬ng lµ :
Bµi tËp lín: LT§KT§
Sinh viªn : Tạ Văn Tiến_
DHDI7TH
3
3222
2
33 /])[]1[.2]2[(5.6][]1[.(]2[ AkYkYkYTkYCkYBkY +++++-+-=+
VËy ph- ¬ng tr×nh sai ph©n m« t¶ hÖ thèng theo ph- ¬ng ph¸p sè Tustin lµ :
322233
1212222
11111
/]))1[][*2]1[(***5.6]1[*][*(]1[
][*]1[*][*]1[
][*]1[*][*]1[
]
[
*
03125
0
]
[
AkYkYkYTTkYCkYBkY
kYBkYBkYAkY
kEBkEBkYAkY
k
Y
U
k
E
-++++---=+
+++=+
+++=+
-
=
§Ó tÝnh qu¸ tr×nh qu¸ ®é cña hÖ thèng ta dïng Matlab ®Ó kiÓm tra xem hÖ thèng cã æn
®Þnh hay kh«ng :
nh- sau :
>> w1=tf([14.5],[3.77 1]);
Transfer function:
14.5
----------
3.77 s + 1
>> w2=tf([25],[.01 1])
Transfer function:
25
----------
0.01 s + 1
>> w3=tf([6.5],[0.04 .3 1])
Transfer function:
6.5
--------------------
0.045 s^2 + 0.3 s + 1
Transfer function:
2356,25
-----------------------------------------------------
Bµi tËp lín: LT§KT§
Sinh viªn : Tạ Văn Tiến_
DHDI7TH
4
0,001697s^4 + 0,1814 s^3 + 1,2161s^2 + 4,08 s + 1
>> k= 0.03125;
>> wk=feedback(wh,k)
Transfer function:
2356,25
-----------------------------------------------------------------------
0,01697s^4 + 0,1814 s^3 + 1,2167s^2 + 4,48s +51,78
>> step(wk)
ta cã ®Æc tÝnh qu¸ ®é nh- sau :
tÝnh qu¸ tr×nh qu¸ ®é b»ng ph- ¬ng ph¸p TUSTIN:
#include<iostream.h>
#include<conio.h>
#include<graphics.h>
include<stdlib.h>
float T,a1a,a2,a3,b1,b2,b3,c3,u;
float y1[640] , y2[640] , y[640] , e[640] ;
int gt , gm , i , k;
void main()
{
co ut<< “\nTinh q u a trin h qua do he thong”;
cout<<”\nnhap buo c tinh T=”; cin >>T;
y[0] = 0; y[1]= 0; y1[0] = 0; y2[0] = 0;
for(k=0; k<=630; k++)
{
Bµi tËp lín: LT§KT§
Sinh viªn : Tạ Văn Tiến_
DHDI7TH
5
;/]))1[][*2]1[(***5.6]1[*][*(]1[
];[*]1[*][*]1[
];[*]1[*][*]1[
];
[
*
03125
0
]
[
322233
1212222
11111
AkYkYkYTTkYCkYBkY
kYBkYBkYAkY
kEBkEBkYAkY
k
Y
U
k
E
-++++---=+
+++=+
+++=+
-
=
co ut<< “\n\t\tk=%3d y=%6.2f “,k,y[k] ;
delay(1) ;
}
getch() ;
gd = DETECT;
initgrap h(&gd,&g m,”c:\\borlandc++\\bgi”) ;
setlinestyle(0,0,3) ;
setbkcolor(0) ; setcolor(4) ;
outtextxy(160,30,”P HUONG P HAP S O TUS TIN”) ;
outtextxy(150,40,”(He khong on dinh )”) ;
outtexexy(20,450,”0”) ;
setcolor(5) ;
rectangle(2,2,637,477) ;
setcolor(1) ;
for (i = i ; i<=10 ; i++)
{
line(64*i, 5, 64*i,15) ;
line(64*i + 32, 5, 64*i + 32, 10) ;
line(64*i, 475, 64*i, 464) ;
line(64*i + 32475, 64*i + 32 , 468) ;
line(5, 48*i, 10 , 48*i) ;
}
setcolor(2) ;
moveto(1,477) ;
for (k=0 ;k<= 630 ; k++)
{
lineto(k, 479 – (int)(10*y[k]/1.6)) ;
}
outtextxy(580, 470 – (int)(10*y[k]/1.6),”y(t)”) ;
outtextxy(455, 450 – (int)(10*y[k]/1.6),”Tin hieu ra”) ;
getch() ;
closegraph() ;
return(0) ;}
3. Khi cã bé PID vµ cã kh©u W4(p) :
a, khi bá kh©u W4(p) ta cã s¬ ®å khèi cña hÖ thèng nh- sau :
Khi m¾c nèi tiÕp bé PID