
1
LỜI GIẢI MỘT SỐ BÀI TẬP
TOÁN CAO CẤP 2
Lời giải một số bài tập trong tài liệu này dùng để tham khảo. Có một số bài tập do
một số sinh viên giải. Khi học, sinh viên cần lựa chọn những phương pháp phù
hợp và đơn giản hơn. Chúc anh chị em sinh viên học tập tốt
BÀI TẬP VỀ ĐỊNH THỨC
Bài 1
Tính các định thức cấp 2:
1) D = 37
25 = 5.3 – 7.2 = 15 – 14 = 1
2) D = 58
23 = 3.5 – 8.2 = 15 – 16 = -1
3) D = 1nn
n1n
= (n+1)(n-1) – n2 = n2 - 1 - n2 = -1
4) D =
cossin
sincos = cos2
+sin2
= 1
Bài 2:
Tính các định thức cấp 3:
1) D =
341
235
312
= 18+2+60-9-16-15 = 40

2
2) D =
243
352
123
= 30+18+8-15-36-8 = -3
3) D =
571
823
534
= 40-24-105+10+224-45=100
4) D =
325
214
423
=-9-20-32+20+12+24= -5
5) D =
631
321
111
= 12 + 3 + 3 – 2 – 9 – 6 = 1
6)
a b
b c
c a
a b c
D b c a
c a b
3 3 3 3 3 3
3
acb bac cba c a b abc c a b
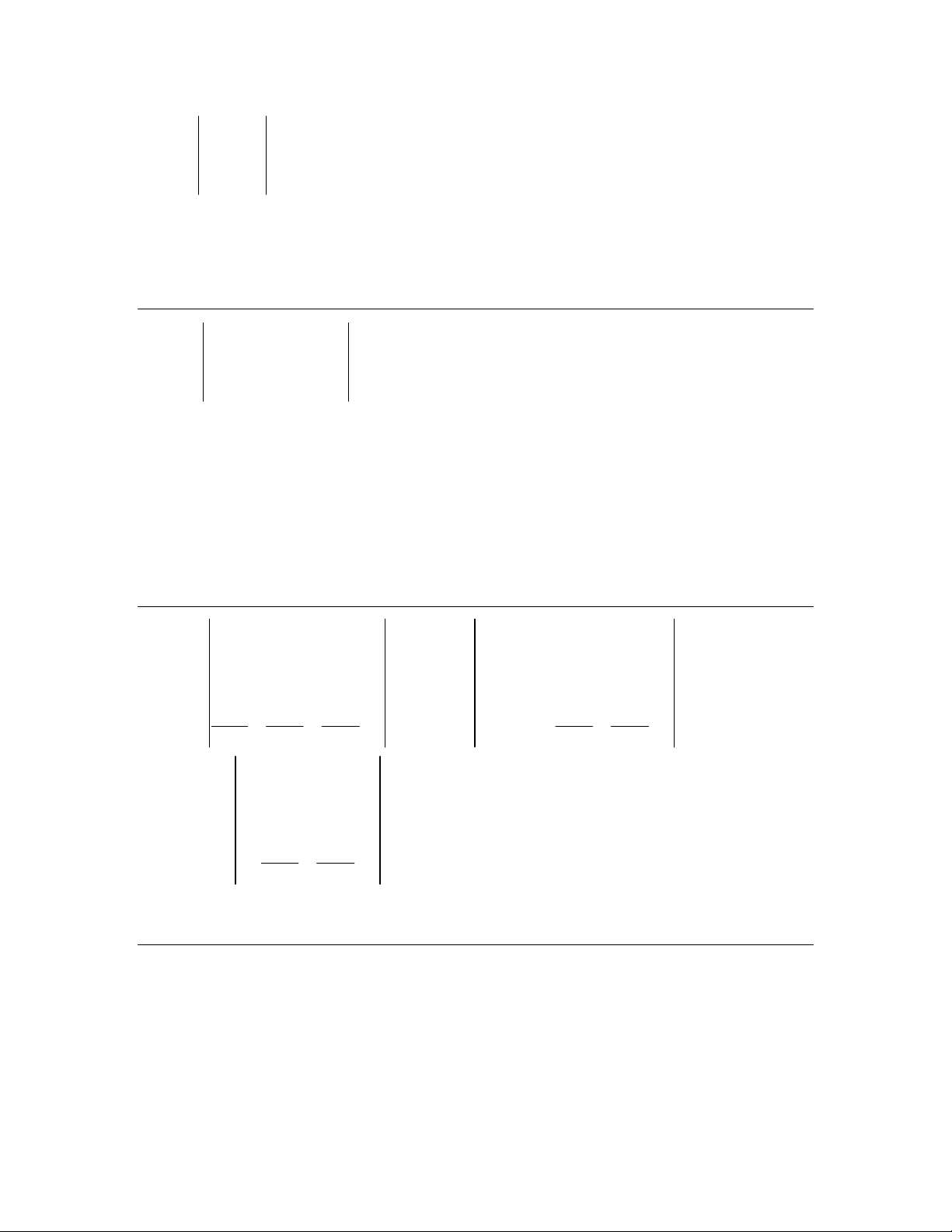
7) D =
0e0
dcb
0a0
= 0
3
8)
a x x a x
D x b x x b
x x c x x
3 3 2 2 2 3 2
2
abc x x bx ax cx abc x x a b c
9)
a x x x a x x
D x b x x x b x
x x c x x x
3 3 2 2 2
2 3 3 2 3 2 3 2 3
2 2 2 3 3 3 2 3 2 3 2 3
a x b x c x x x x b x x a x x c x
ab ax bx x c x x x bx x x a x x c x
abc abx acx ax bcx bx cx x x x bx x x a x x c x
abc abx acx bcx
3 2 1
1 1
1 1
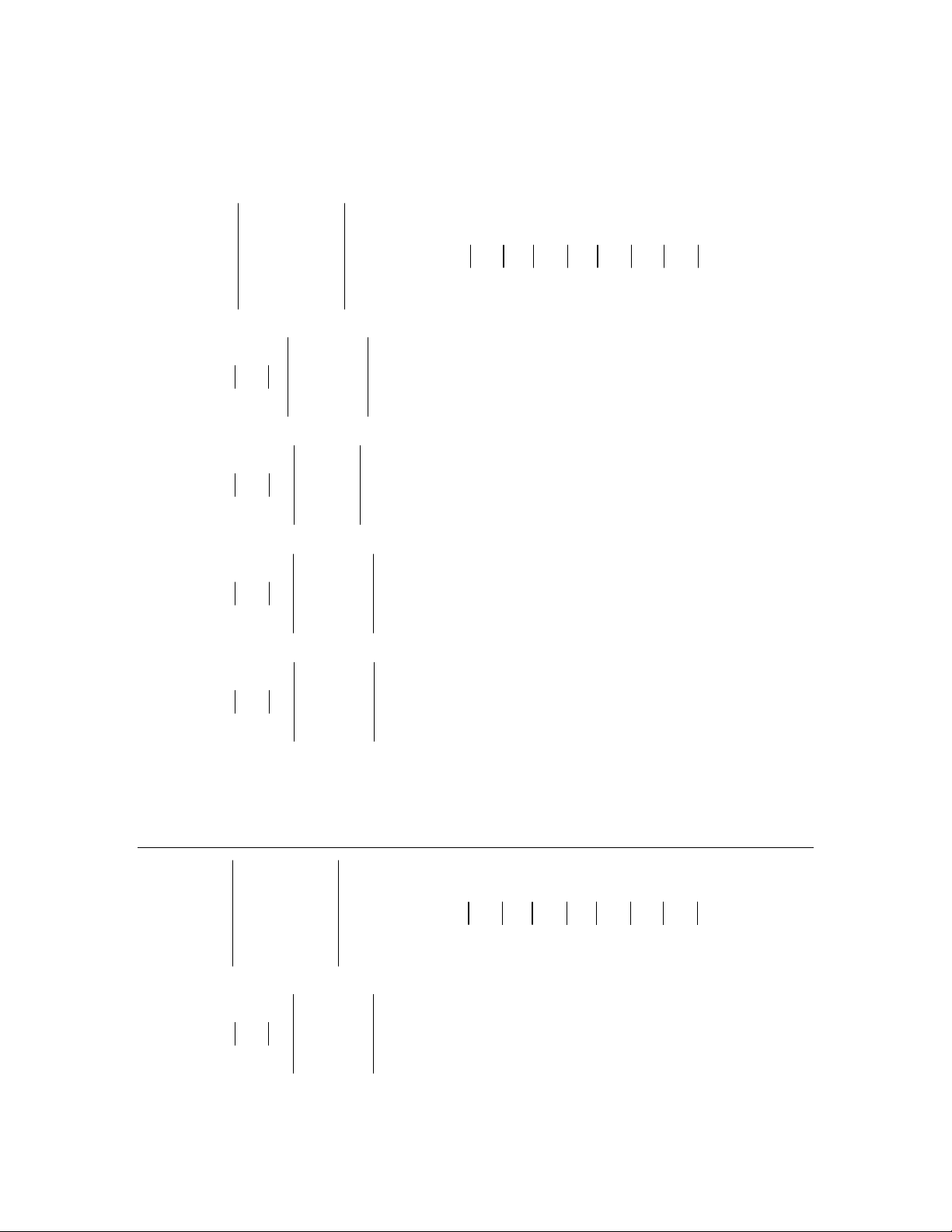
10)
1 1
1 1
2 2 2 2 2
1 1
1 1
0
1 1
1 1
2 2
c c c
a b c a b c b c
b c a b c a c a
Dc a b c a b a b
b c c a a b c a a b
a b c
b c
c a
a b c a b
c a a b
4
Bài 3
Tính các định thức:
1) 33 1
31 32 33 34
2 3 4 1
4 2 3 2 ( 1)
3 1 4 3
h
D a M b M c M d M
a b c d
* 31
M=
341
232
143
= -27 -8 -8 + 3 +24 + 24 = 8
* 32
M=
343
234
142
= 18 + 24 + 16 – 9 – 16 – 48 = -15
* 33
M=
313
224
132
= -12 – 18 – 4 + 6 +4 +36 = 12
* 34
M=
413
324
432
= -16 -27 – 16 + 24 + 6 +48 = 19
Vậy: D = 8a+15b+12c-19d
2)
2 1
2
21 22 23 24
5 2 1
4 4 3 1
2 3 2
4 5 4
c
a
b
D a M b M c M d M
c
d
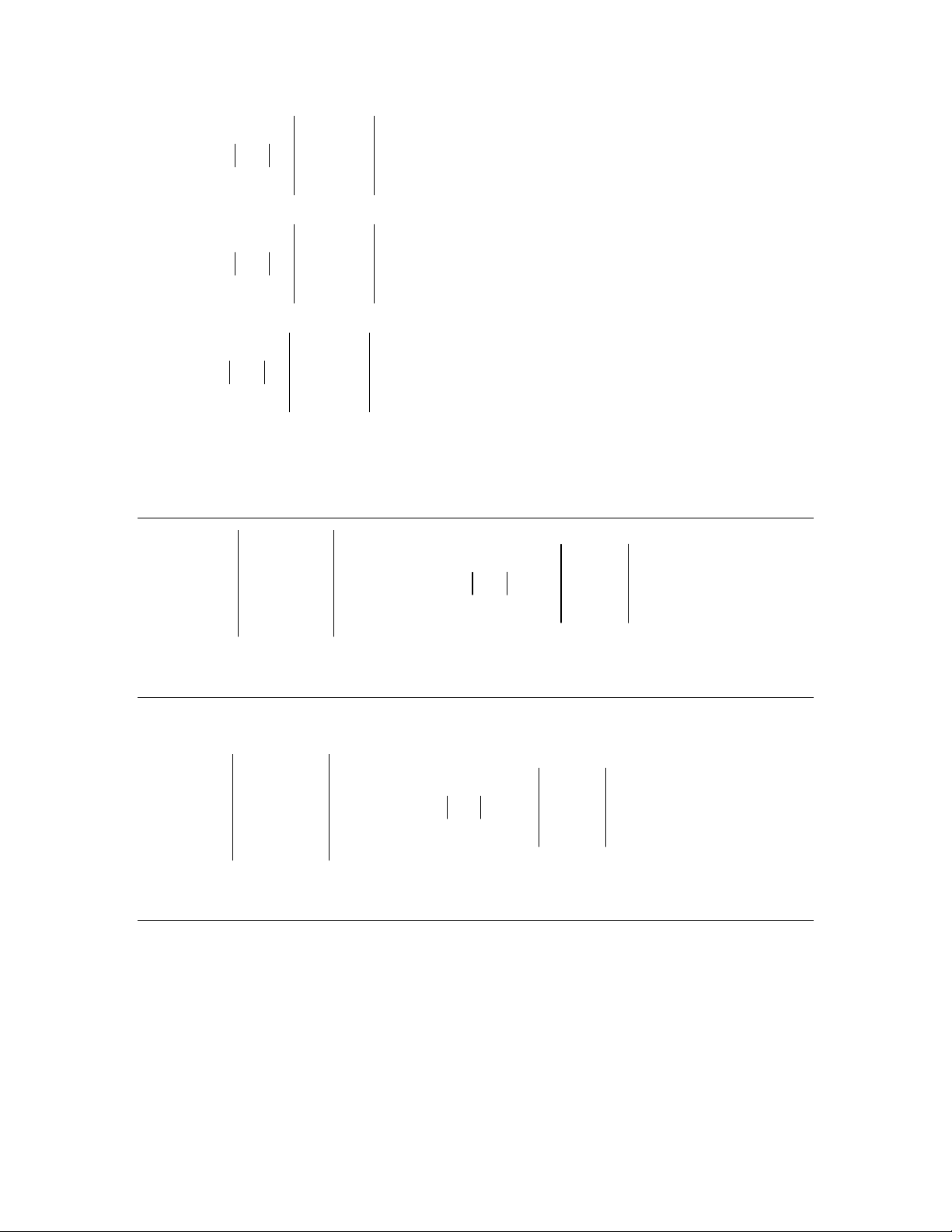
* 12
M=
454
232
344
= -48 – 32 – 30 + 36 + 40 + 32 = -2
5
* 22
M=
454
232
125
= -60 -16 – 10 + 12 + 50 +16 = -8
* 32
M=
454
344
125
= -80 – 24 – 20 + 16 + 75 + 32 = -1
*42
M=
232
344
125
= -40 -12 – 12 + 8 + 45 + 16 = 5
Vậy: D = - (-2a + 8b – c - 5d) = 2a - 8b + c + 5d
3)
44 1
44
3 0 5 3 0
0 0 2 ( 1) 0 0
1 2 3 1 2
0 0 0
h
aa
b
D d M d b abcd
cc
d
4)
44 1
41
1 0 2 0 2
2 0 0 ( 1) 0 0
3 4 5 4 5
0 0 0
h
aa
b
D d M d b abcd
cc
d






















![Đề thi cuối kì môn Mô hình hóa toán học [kèm đáp án]](https://cdn.tailieu.vn/images/document/thumbnail/2026/20260121/lionelmessi01/135x160/83011768986868.jpg)



