Bµi tËp m«n §iÖn tö sè
Ch¬ng 1. C¸c kh¸i niÖm c¬ b¶n
Bµi 1. Dïng c¸c hµm logic c¬ b¶n (AND, OR, NOT) viÕt l¹i c¸c hµm sau:
a) Y = A ⊕ B ⊕ C b) Y = A ⊕ B ⊕ C ⊕ D
c) Y = A ⊕ B ~ C d) Y =
D~CBA ⊕⊕
Bµi 2. Chøng minh c¸c biÓu thøc sau:
a)
D).CB.(ADBCA +=++
b)
C).BA(CB.AAB ⊕=++
c)
1ABB.AB.AB.A =+++
d)
CBACBA ⊕⊕=⊕⊕
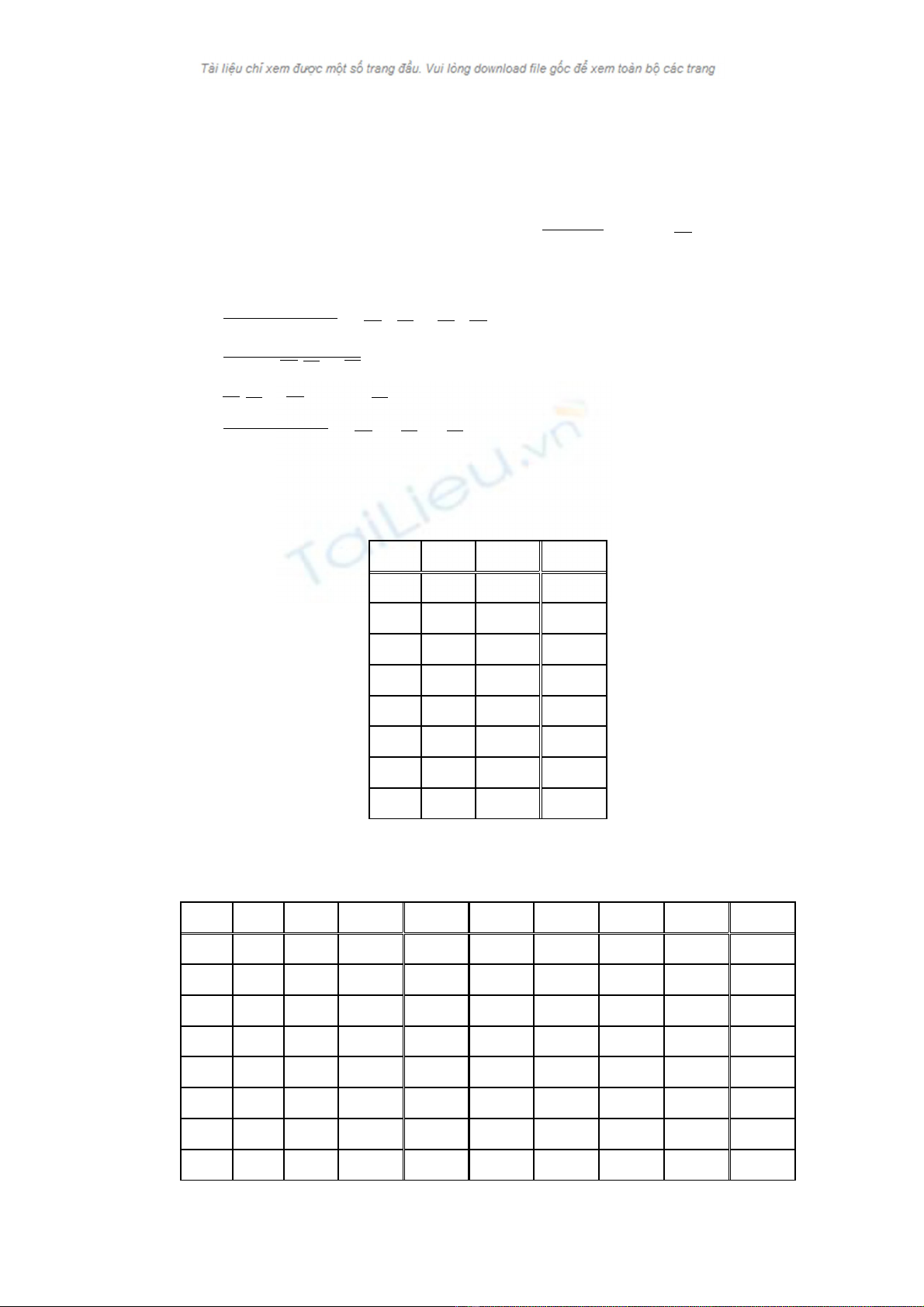
Bµi 3. BiÓu diÔn hµm sè sau díi d¹ng chuÈn t¾c héi:
A B C Y
0 0 0 1
0 0 1 0
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 ×
1 1 0 0
1 1 1 1
Bµi 4. BiÓu diÔn hµm sè sau díi d¹ng chuÈn t¾c tuyÓn:
A B C D Y A B C D Y
0 0 0 0 1 1 0 0 0 1
0 0 0 1 0 1 0 0 1 0
0 0 1 0 0 1 0 1 0 1
0 0 1 1 1 1 0 1 1 1
0 1 0 0 0 1 1 0 0 0
0 1 0 1 ×1101×
0 1 1 0 0 1 1 1 0 0
0 1 1 1 0 1 1 1 1 0
Bµi 5. BiÓu diÓn hµm sau dïng b¶ng Karnaugh:

A B C D Y A B C D Y
00 0 0 1 10 0 0 1
00 0 1 ×10 0 1 0
00 1 0 0 10 1 0 1
00 1 1 1 1011×
01 0 0 0 11 0 0 0
01 0 1 1 1101×
01 1 0 1 11 1 0 0
01 1 1 0 11 1 1 1
Bµi 6. BiÓu diÔn c¸c hµm sau dïng b¶ng Karnaugh:
a)
DCBAN,ABCDDCBADCBADCBADCBAY =++++=
b)
CBAN),CBA)(CBA)(CBA)(CBA(Y ++=++++++++=
Bµi 7. BiÓu diÔn c¸c hµm sau dïng b¶ng Karnaugh:
a) Y(A, B, C, D) = m0 + m2 + m3 + m9 + m10 + m11, N = m1 , m4 , m13
b) Y(A, B, C, D) = M1. M2. M5. M8. M14, N = M4. M9. M15
Bµi 8. BiÓu diÔn c¸c hµm sau dïng b¶ng Karnaugh:
a) Y(A, B, C, D) = Σ(0, 1, 5, 6, 10, 11, 13) N = 4, 7, 14
b) Y(A, B, C, D) = Π(1, 4, 8, 10, 15) N = 3, 9, 14
Bµi 9. BiÓu diÔn c¸c hµm sau dïng b¶ng Karnaugh:
a)
DBACB).CDAB(Y +⊕=
b)
)CAD)(BAC(Y +⊕=
Bµi 10. Dïng b¶ng Karnaugh tèi thiÓu ho¸ hµm sau:
a) Y(A, B, C, D) = Σ(0, 1, 2, 8, 9, 13, 14, 15) N = 10, 11
b) Y(A, B, C, D) = Π(0, 4, 7, 8, 13, 15) N = 2, 9, 14
Bµi 11. Dïng b¶ng Karnaugh tèi thiÓu ho¸ hµm sau:
a)
,DCBABCDADCBADCBACDBADCBAY +++++=
DBCA,DCBAN =
b)
),DCBA)(DCBA)(DCBA)(DCBA(Y ++++++++++++=
DCBA,DCBA,DCBA,DCBAN ++++++++++++=
Bµi 12. Dïng b¶ng Karnaugh tèi thiÓu ho¸ hµm sau:
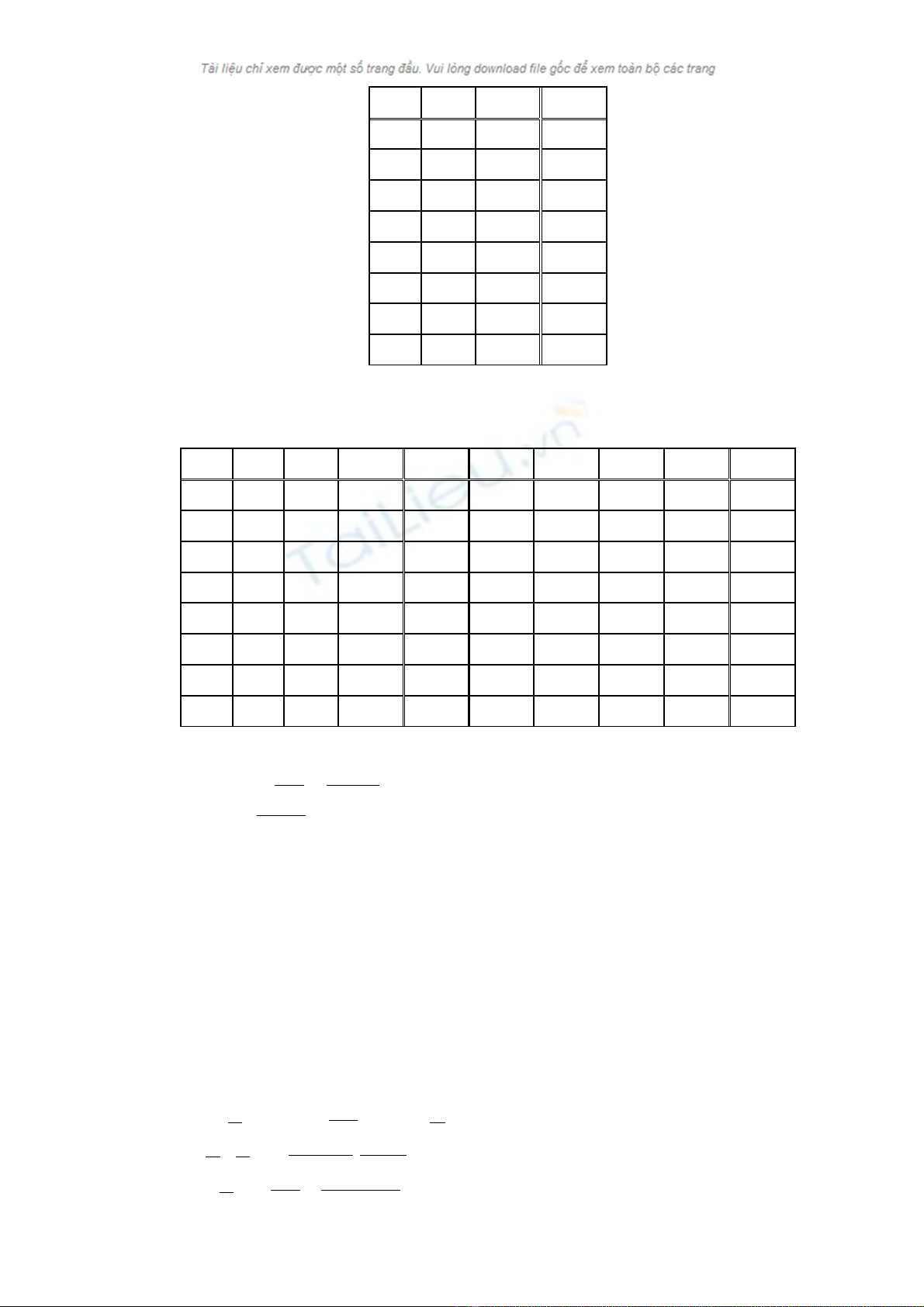
A B C Y
0 0 0 1
0 0 1 0
0 1 0 1
0 1 1 1
1 0 0 0
1 0 1 1
1 1 0 ×
1 1 1 1
Bµi 13. Dïng b¶ng Karnaugh tèi thiÓu ho¸ hµm sau:
A B C D Y A B C D Y
00 0 0 1 1000×
00 0 1 ×10 0 1 1
00 1 0 1 10 1 0 1
00 1 1 1 1011×
01 0 0 0 11 0 0 1
01 0 1 0 11 0 1 0
01 1 0 ×11 1 0 1
01 1 1 1 11 1 1 0
Bµi 14. Dïng b¶ng Karnaugh tèi thiÓu ho¸ hµm sau:
a)
DACDABCY ++⊕=
b)
BDBC~ACY ++=
Bµi 15. Dùa vµo b¶n chÊt cña tÝn hiÖu ®iÖn vµo vµ ra, cã c¸c lo¹i IC
nµo
Bµi 16. Dùa vµo mËt ®é tÝch hîp, cã c¸c lo¹i IC nµo, ®Æc ®iÓm cña
mçi lo¹i.
Bµi 17. Dùa vµo c«ng nghÖ chÕ t¹o, cã c¸c lo¹i IC nµo.
Bµi 18. VÏ s¬ ®å logic cña c¸c hµm sau:
a)
DBCA.BD)ACBA(Y +⊕+=
b)
ABBCD.CABDCBAY ⊕++=
c)
DE~AB.ECDCBAY +=

Ch¬ng 2. M¹ch tæ hîp
Bµi 1. H·y thiÕt kÕ m¹ch trõ ®ñ 1 bit
Bµi 2. H·y thiÕt kÕ m¹ch tæ hîp, ®Çu vµo DCBA lµ sè nhÞ ph©n 4 bit,
®Çu ra lµ Y biÓu diÔn tÝnh chia hÕt cña DCBA cho 4.
Bµi 3. H·y thiÕt kÕ m¹ch nh©n hai sè A vµ B gièng phÐp nh©n tay
th«ng thêng, víi A, B lµ hai sè 2 bit.
Bµi 4. H·y lËp b¶ng ch©n lý cña bé so s¸nh hai sè A vµ B 2 bit.
Bµi 5. H·y vÏ s¬ ®å cña m¹ch céng ®ñ (FA) chØ dïng m¹ch NAND.
Bµi 6. H·y thiÕt kÕ m¹ch m· ho¸ tõ thËp ph©n thµnh m· 7 thanh.
Bµi 7. H·y thiÕt kÕ m¹ch chuyÓn m· tõ m· nhÞ ph©n 4 bit thµnh m·
Gray 4 bit.
Bµi 8. H·y thiÕt kÕ m¹ch gi¶i m· tõ m· Gray thµnh m· thËp ph©n.
Bµi 9. H·y thiÕt kÕ m¹ch chuyÓn m· tõ m· Gray 4 bit thµnh m· nhÞ
ph©n 4 bit.
Bµi 10. H·y thiÕt kÕ m¹ch gi¶i m· tõ m· nhÞ ph©n thµnh m· thËp ph©n.
Bµi 11. H·y thiÕt kÕ m¹ch t¹o bit ch½n lÎ (hÖ ch½n) ®èi víi m¹ch cã 4
®Çu vµo d÷ liÖu.
Bµi 12. H·y thiÕt kÕ m¹ch kiÓm tra tÝnh ch½n lÎ (hÖ lÎ) víi 3 ®Çu vµo
d÷ liÖu vµ 1 ®Çu vµo ch½n lÎ.
Bµi 13. H·y thiÕt kÕ m¹ch ROM chuyÓn m· tõ m· Gray 2 bit thµnh m·
nhÞ ph©n 2 bit.
Bµi 14. H·y thiÕt kÕ bé dån kªnh 8 -> 1.
Bµi 15. H·y thiÕt kÕ bé ph©n kªnh 1-> 8.
Bµi 16. H·y thiÕt kÕ m¹ch chuyÓn m· tõ m· BCD thµnh m· thõa 3.
Bµi 17. H·y thiÕt kÕ m¹ch chuyÓn m· tõ m· thõa 3 thµnh m· BCD.
Ch¬ng 3. M¹ch lËt
Bµi 1. B¶ng ch©n lý díi ®©y lµ cña m¹ch lËt nµo? A, B lµ g×?
A B Qn
0 1 1
1 0 0
0 0 Qn -1
1 1 ×
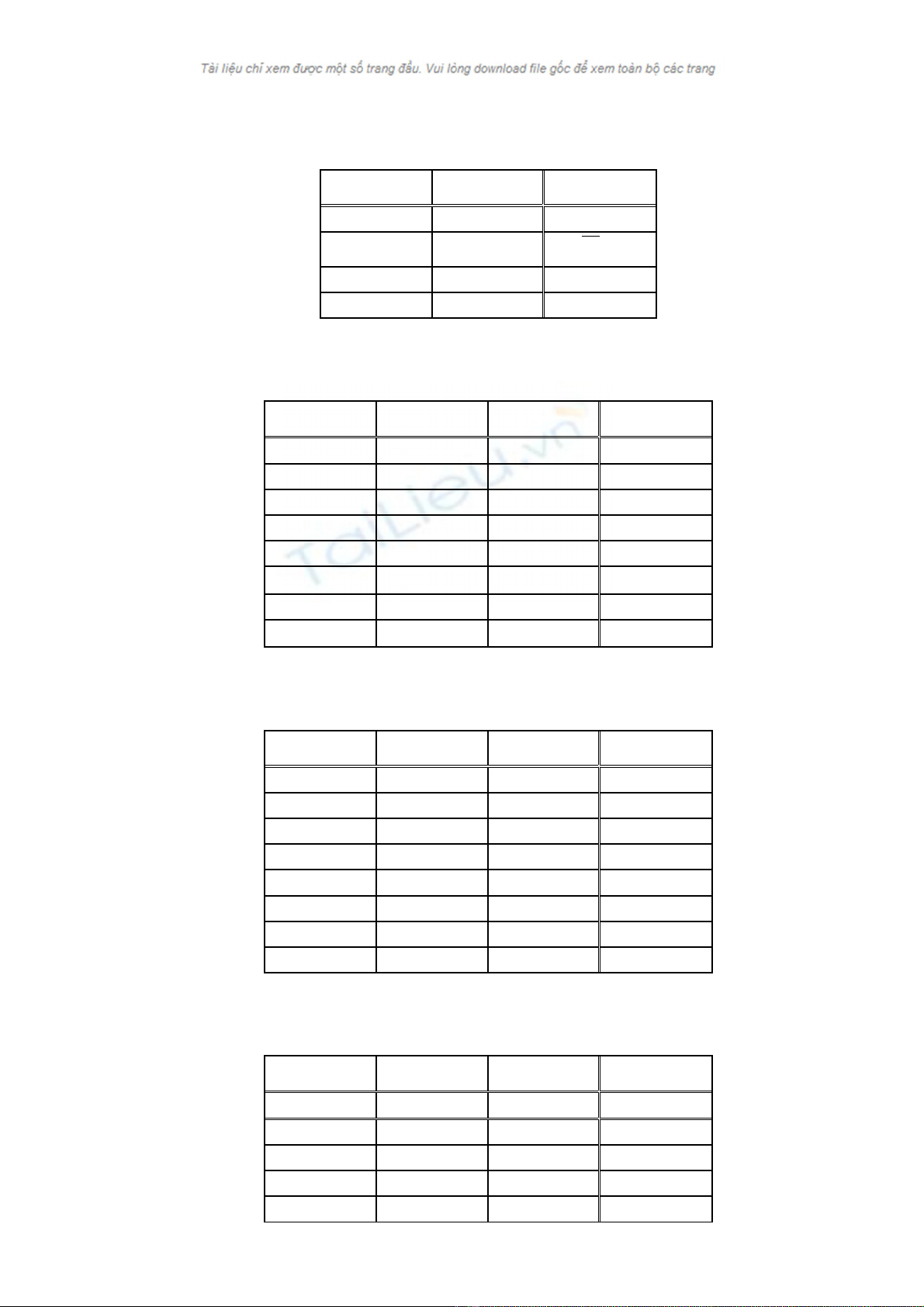
Bµi 2. B¶ng ch©n lý díi ®©y lµ cña m¹ch lËt nµo? A, B lµ g×?
A B Qn
0 0 Qn -1
1 1
1n
Q−
0 1 1
1 0 0
Bµi 3. B¶ng ch©n lý díi ®©y lµ cña m¹ch lËt nµo? A, B lµ g×?
A B Qn -1 Qn
0 0 0 0
0 1 1 1
0 0 1 1
0 1 0 1
1 0 1 0
110×
1 0 0 0
111×
Bµi 4. B¶ng ch©n lý díi ®©y lµ cña m¹ch lËt nµo? A, B lµ g×?
A B Qn -1 Qn
0 0 0 0
0 1 1 1
0 1 0 1
0 0 1 1
1 0 0 0
1 1 0 1
1 0 1 0
1 1 1 0
Bµi 5. B¶ng ch©n lý díi ®©y lµ cña m¹ch lËt nµo? A, B lµ g×, nhÞp g×?
NhÞp A B Qn
0 0 1 Qn – 1
0 0 0 Qn – 1
0 1 1 Qn – 1
0 1 0 Qn – 1
1 1 0 0