C U TRÚC D LI U VÀ Ấ Ữ Ệ
GI I THU TẢ Ậ
Ch ng 11: Cây đa phânươ
Ch ng 11: Cây đa phânươ
2
Đ nh nghĩaị
Cây đa phân
Cây r ngỗ
Ho c có m t node g i là g c (root) và nhi u cây con.ặ ộ ọ ố ề
Bi u di n:ể ễ
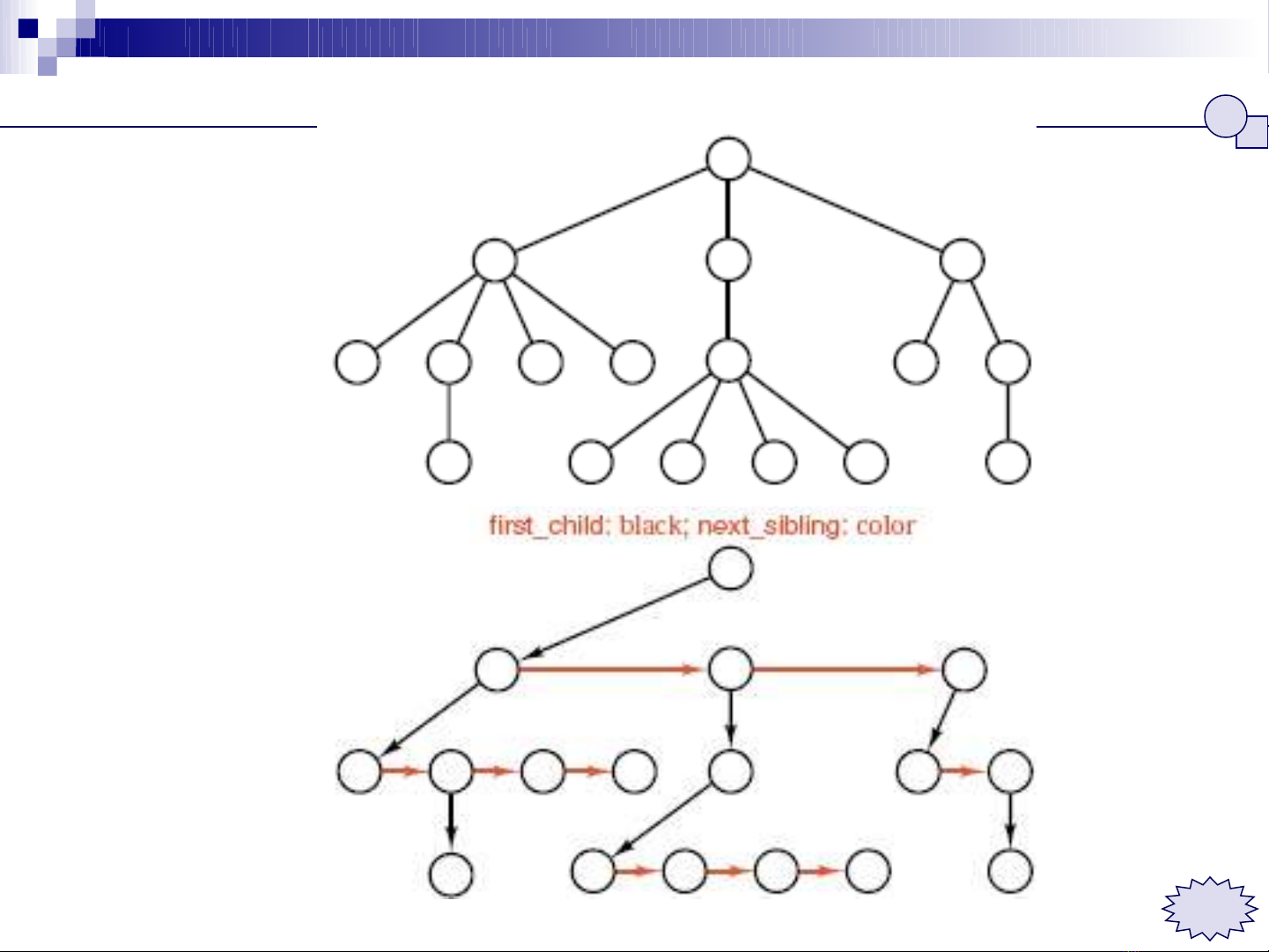
M i node g m có nhi u nhánh conỗ ồ ề
M i node có 2 liên k t first_child và next_siblingỗ ế
Dùng cây nh phânị
Ch ng 11: Cây đa phânươ
3
Bi u di nể ễ
Ch ng 11: Cây đa phânươ
4
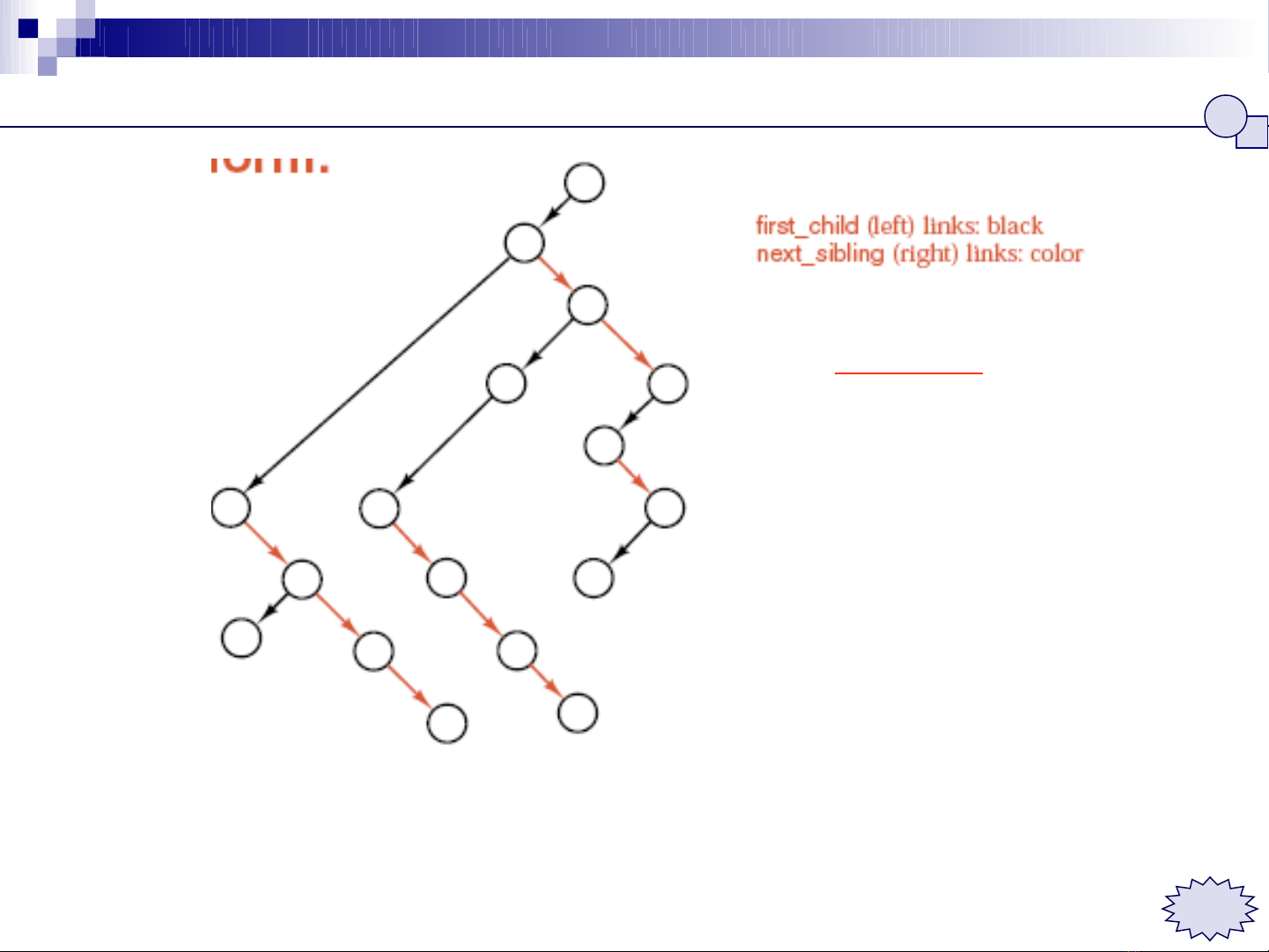
Bi u di n d ng nh phânể ễ ạ ị
Nh phân:ị
left = black
right = color
Ch ng 11: Cây đa phânươ
5
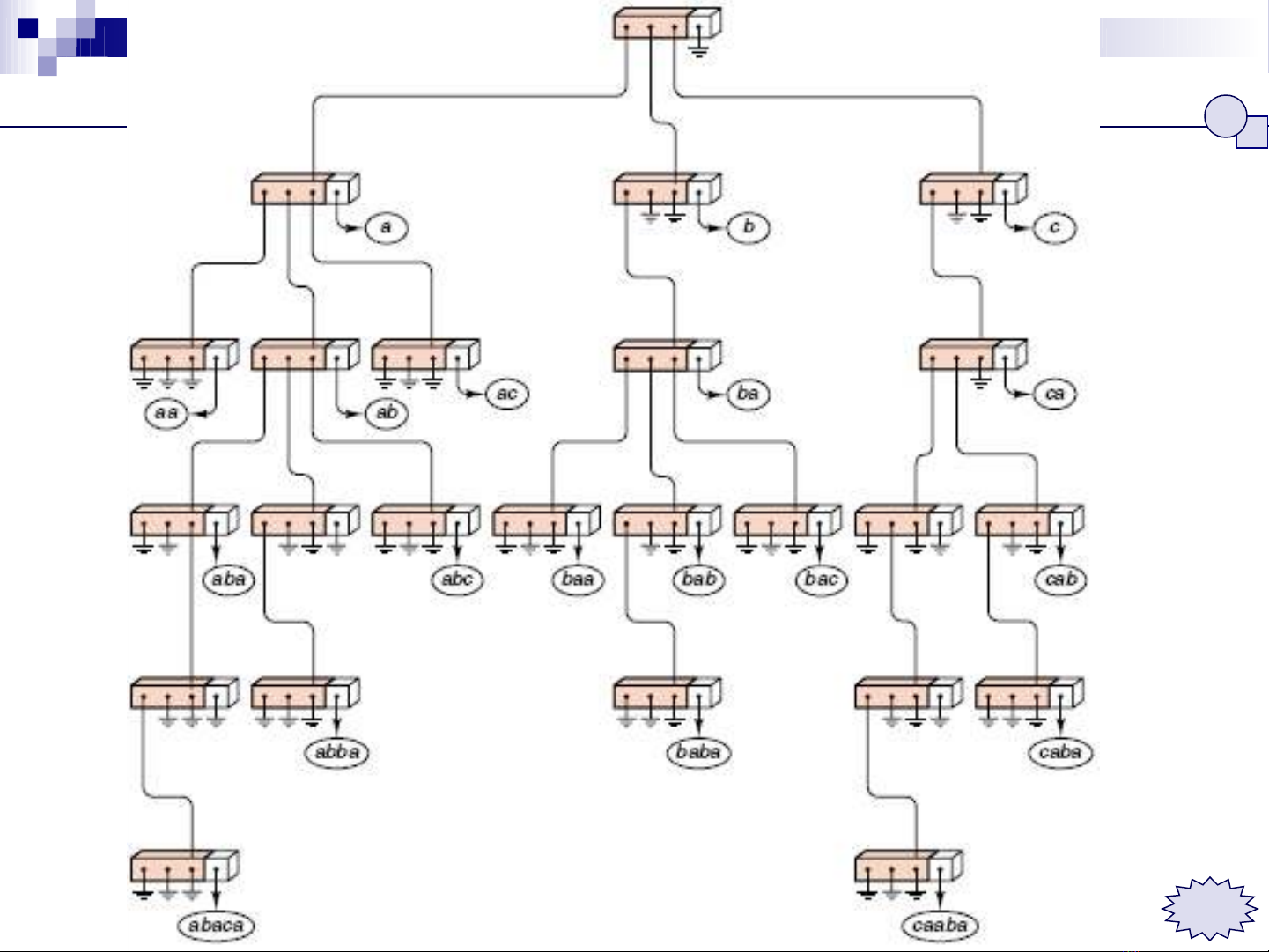
Cây t đi n: Trieừ ể