Tr ng Đ i h c Bách khoa tp. H Chí Minhườ ạ ọ ồ
B môn Toán ng d ngộ Ứ ụ
-------------------------------------------------------------------------------------
Gi i tích hàm nhi u bi n ả ề ế
Ch ng 4ươ : Tích phân b i baộ
•Gi ng viên Ts. Đ ng Văn Vinh (4/2008)ả ặ
dangvvinh@hcmut.edu.vn
N i dungộ
---------------------------------------------------------------------------------------------------------------------------
0.2 – T a đ trọ ộ ụ
0.3 – T a đ c uọ ộ ầ
0.1 – Đ nh nghĩa, cách tính tích phân b i baị ộ
0.5 – ng d ng c h cỨ ụ ơ ọ
0.4 – ng d ng hình h cỨ ụ ọ
I. Đ nh nghĩa, cách tính tích phân b i ba ị ộ
---------------------------------------------------------------------------------------------------------------------------
( , , )f f x y z=
xác đ nh trên v t th đóng, b ch n ị ậ ể ị ặ
E
Chia E m t cách tùy ý ra thành n kh i nh : ộ ố ỏ 1 2
, ,..., .
n
E E E
Th tích t ng ng m i kh i ể ươ ứ ỗ ố
1 2
( ), ( ),..., ( ).
n
V E V E V E
Trên m i kh i l y tuỳ ý m t đi m ỗ ố ấ ộ ể ( , , ).
i i i i
M x y z
i
E
L p t ng Riemann: ậ ổ
1
( ) ( )
n
n i i
i
I f M V E
=
=
, không ph thu c cách chia ụ ộ E, và cách l y đi m ấ ể Mi
lim n
n
I I
+
=
đ c g i là ượ ọ tích phân b i baộ c a ủf=f(x,y,z) trên kh i ốE.
( , , )
E
I f x y z dxdydz=���
I. Đ nh nghĩa, cách tính tích phân kép ị
---------------------------------------------------------------------------------------------------------------------------
Tính ch t c a tích phân b i baấ ủ ộ
1) Hàm liên t c trên m t kh i đóng, b ch n, có biên là m t tr n tùng khúc ụ ộ ố ị ặ ặ ơ
thì kh tích trên mi n này. ả ề
3) ( , , ) ( , , )
E E
f x y z dxdydz f x y z dxdydz
α α
=�
��� ���
2)
E
E
V dxdydz
=���
4) ( )
E E E
f g dxdydz f dxdydz gdxdydz+ = +
��� ��� ���
5) N u ếE đ c chia làm hai kh i ượ ố E1 và E2 không d m lên nhau: ẫ
1 2
E E E
fdxdydz fdxdydz fdxdydz= +
��� ��� ���
6) ( , , ) , ( , , ) ( , , )
E E
x y z E f x y z g x y z f g∀ Σ
��� ���
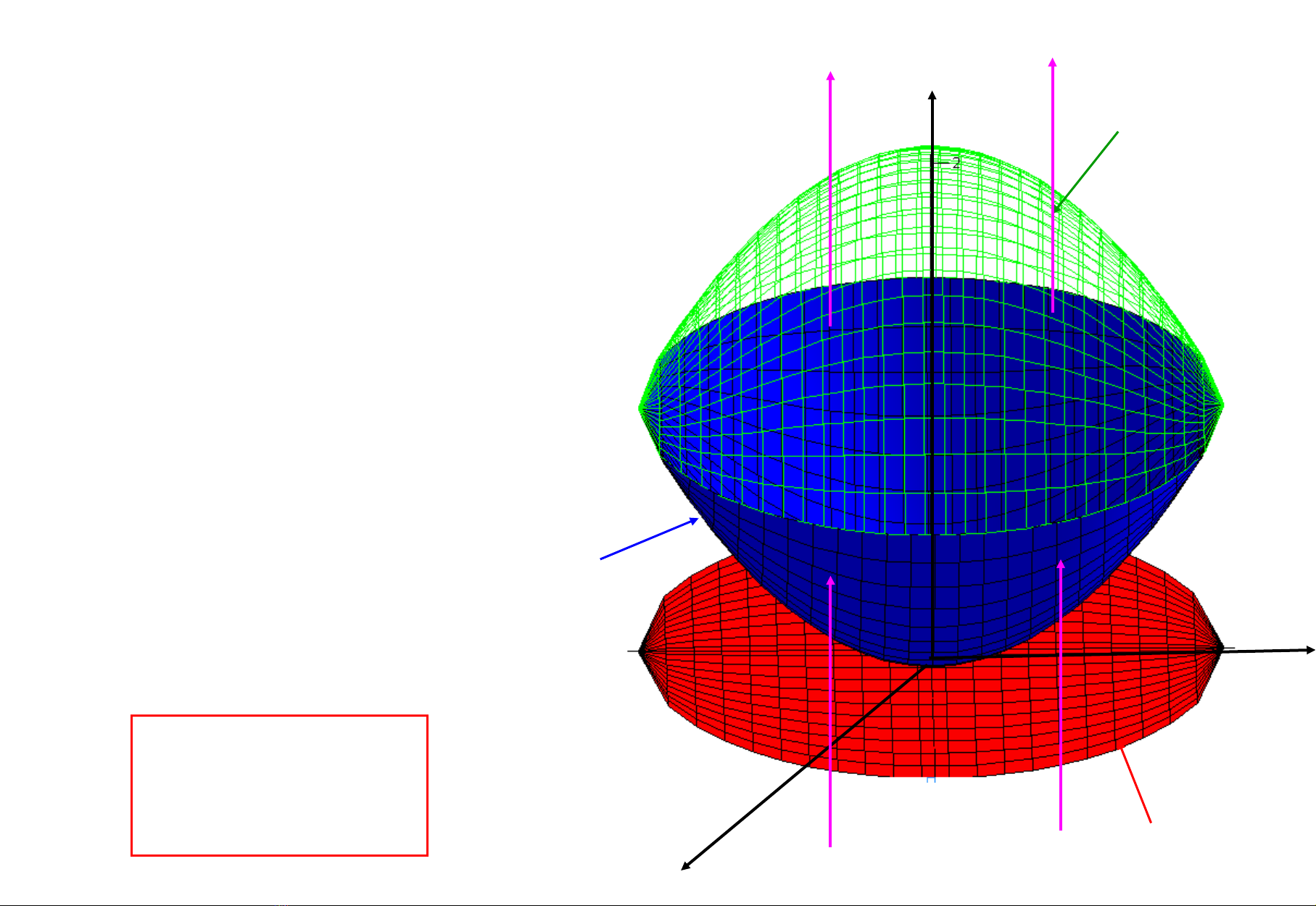
Đ nh lý (Fubini)ị
( , , )
E
I f x y z dxdydz=���
Phân tích kh i ốE:Ch n m t chi u là x0y.ọ ặ ế
M t phía trên:ặ
2( , )z z x y=
1( , )z z x y=
M t phía d i:ặ ướ
Hình chi uế:
Hình chi uế: D
2
1
( , )
( , )
( , , )
z x y
D z x y
f x y z dz dxdy
� �
=�� �
� �
� �
( , , )
E
I f x y z dxdydz=���
2( , )z z x y=
1( , )z z x y=
0
Pr xy E D=